给定一个有向图和其中的两个顶点“u”和“v”,计算从“u”到“v”的所有可能的走行,走行上正好有k条边。 给出了图表 邻接矩阵表示法 其中,图[i][j]的值为1表示从顶点i到顶点j有一条边,值为0表示从i到j没有边。
null
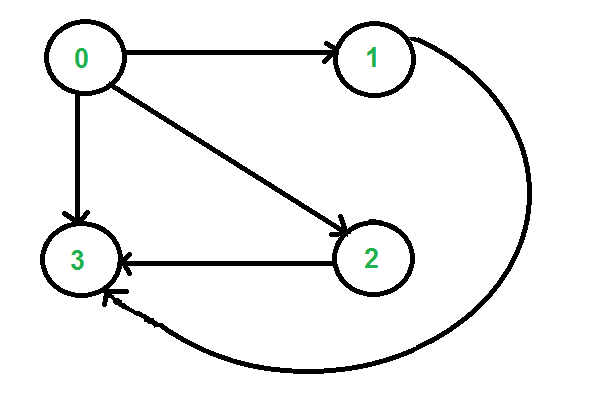
例如,考虑下面的图表。让源“u”为顶点0,目标“v”为3,k为2。输出应该是2,因为从0到3有两次行走,正好有两条边。步行是{0,2,3}和{0,1,3}
简单方法 :创建一个递归函数,用于获取当前顶点、目标顶点和顶点计数。使用当前顶点的所有相邻顶点调用递归函数,该顶点的k值为k-1。当k的值为0时,检查当前顶点是否为目标。如果是destination,则输出答案为1。
下面是这个简单解决方案的实现。
C++
// C++ program to count walks from u to // v with exactly k edges #include <iostream> using namespace std; // Number of vertices in the graph #define V 4 // A naive recursive function to count // walks from u to v with k edges int countwalks( int graph[][V], int u, int v, int k) { // Base cases if (k == 0 && u == v) return 1; if (k == 1 && graph[u][v]) return 1; if (k <= 0) return 0; // Initialize result int count = 0; // Go to all adjacents of u and recur for ( int i = 0; i < V; i++) if (graph[u][i] == 1) // Check if is adjacent of u count += countwalks(graph, i, v, k - 1); return count; } // driver program to test above function int main() { /* Let us create the graph shown in above diagram*/ int graph[V][V] = { { 0, 1, 1, 1 }, { 0, 0, 0, 1 }, { 0, 0, 0, 1 }, { 0, 0, 0, 0 } }; int u = 0, v = 3, k = 2; cout << countwalks(graph, u, v, k); return 0; } |
JAVA
// Java program to count walks from u to v with exactly k edges import java.util.*; import java.lang.*; import java.io.*; class KPaths { static final int V = 4 ; // Number of vertices // A naive recursive function to count walks from u // to v with k edges int countwalks( int graph[][], int u, int v, int k) { // Base cases if (k == 0 && u == v) return 1 ; if (k == 1 && graph[u][v] == 1 ) return 1 ; if (k <= 0 ) return 0 ; // Initialize result int count = 0 ; // Go to all adjacents of u and recur for ( int i = 0 ; i < V; i++) if (graph[u][i] == 1 ) // Check if is adjacent of u count += countwalks(graph, i, v, k - 1 ); return count; } // Driver method public static void main(String[] args) throws java.lang.Exception { /* Let us create the graph shown in above diagram*/ int graph[][] = new int [][] { { 0 , 1 , 1 , 1 }, { 0 , 0 , 0 , 1 }, { 0 , 0 , 0 , 1 }, { 0 , 0 , 0 , 0 } }; int u = 0 , v = 3 , k = 2 ; KPaths p = new KPaths(); System.out.println(p.countwalks(graph, u, v, k)); } } // Contributed by Aakash Hasija |
Python3
# Python3 program to count walks from # u to v with exactly k edges # Number of vertices in the graph V = 4 # A naive recursive function to count # walks from u to v with k edges def countwalks(graph, u, v, k): # Base cases if (k = = 0 and u = = v): return 1 if (k = = 1 and graph[u][v]): return 1 if (k < = 0 ): return 0 # Initialize result count = 0 # Go to all adjacents of u and recur for i in range ( 0 , V): # Check if is adjacent of u if (graph[u][i] = = 1 ): count + = countwalks(graph, i, v, k - 1 ) return count # Driver Code # Let us create the graph shown in above diagram graph = [[ 0 , 1 , 1 , 1 , ], [ 0 , 0 , 0 , 1 , ], [ 0 , 0 , 0 , 1 , ], [ 0 , 0 , 0 , 0 ] ] u = 0 ; v = 3 ; k = 2 print (countwalks(graph, u, v, k)) # This code is contributed by Smitha Dinesh Semwal. |
C#
// C# program to count walks from u to // v with exactly k edges using System; class GFG { // Number of vertices static int V = 4; // A naive recursive function to // count walks from u to v with // k edges static int countwalks( int [, ] graph, int u, int v, int k) { // Base cases if (k == 0 && u == v) return 1; if (k == 1 && graph[u, v] == 1) return 1; if (k <= 0) return 0; // Initialize result int count = 0; // Go to all adjacents of u and recur for ( int i = 0; i < V; i++) // Check if is adjacent of u if (graph[u, i] == 1) count += countwalks(graph, i, v, k - 1); return count; } // Driver method public static void Main() { /* Let us create the graph shown in above diagram*/ int [, ] graph = new int [, ] { { 0, 1, 1, 1 }, { 0, 0, 0, 1 }, { 0, 0, 0, 1 }, { 0, 0, 0, 0 } }; int u = 0, v = 3, k = 2; Console.Write( countwalks(graph, u, v, k)); } } // This code is contributed by nitin mittal. |
PHP
<?php // PHP program to count walks from u // to v with exactly k edges // Number of vertices in the graph $V = 4; // A naive recursive function to count // walks from u to v with k edges function countwalks( $graph , $u , $v , $k ) { global $V ; // Base cases if ( $k == 0 and $u == $v ) return 1; if ( $k == 1 and $graph [ $u ][ $v ]) return 1; if ( $k <= 0) return 0; // Initialize result $count = 0; // Go to all adjacents of u and recur for ( $i = 0; $i < $V ; $i ++) // Check if is adjacent of u if ( $graph [ $u ][ $i ] == 1) $count += countwalks( $graph , $i , $v , $k - 1); return $count ; } // Driver Code /* Let us create the graph shown in above diagram*/ $graph = array ( array (0, 1, 1, 1), array (0, 0, 0, 1), array (0, 0, 0, 1), array (0, 0, 0, 0)); $u = 0; $v = 3; $k = 2; echo countwalks( $graph , $u , $v , $k ); // This code is contributed by anuj_67. ?> |
Javascript
<script> // Javascript program to count walks from u to // v with exactly k edges // Number of vertices in the graph var V = 4 // A naive recursive function to count // walks from u to v with k edges function countwalks(graph, u, v, k) { // Base cases if (k == 0 && u == v) return 1; if (k == 1 && graph[u][v]) return 1; if (k <= 0) return 0; // Initialize result var count = 0; // Go to all adjacents of u and recur for ( var i = 0; i < V; i++) if (graph[u][i] == 1) // Check if is adjacent of u count += countwalks(graph, i, v, k - 1); return count; } // driver program to test above function /* Let us create the graph shown in above diagram*/ var graph = [[0, 1, 1, 1, ], [0, 0, 0, 1, ], [0, 0, 0, 1, ], [0, 0, 0, 0] ]; var u = 0, v = 3, k = 2; document.write(countwalks(graph, u, v, k)); // This code contributed by shubhamsingh10 </script> |
输出:
2
复杂性分析:
- 时间复杂性: O(V) K ). 上述函数的最坏情况时间复杂度为O(V K )其中V是给定图形中的顶点数。我们可以简单地通过绘制递归树来分析时间复杂度。最坏的情况发生在完整的图形中。在最坏的情况下,递归树的每个内部节点正好有n个子节点。
- 辅助空间: O(V)。 要存储堆栈空间和访问的阵列,需要O(V)空间。
有效方法: 可以使用 动态规划 其想法是建立一个3D表格,其中第一个维度是源,第二个维度是目标,第三个维度是从源到目标的边数,值是行走次数。和其他人一样, 动态规划问题 ,以自下而上的方式填充3D表格。
C++
// C++ program to count walks from // u to v with exactly k edges #include <iostream> using namespace std; // Number of vertices in the graph #define V 4 // A Dynamic programming based function to count walks from u // to v with k edges int countwalks( int graph[][V], int u, int v, int k) { // Table to be filled up using DP. // The value count[i][j][e] will // store count of possible walks from // i to j with exactly k edges int count[V][V][k + 1]; // Loop for number of edges from 0 to k for ( int e = 0; e <= k; e++) { for ( int i = 0; i < V; i++) // for source { for ( int j = 0; j < V; j++) // for destination { // initialize value count[i][j][e] = 0; // from base cases if (e == 0 && i == j) count[i][j][e] = 1; if (e == 1 && graph[i][j]) count[i][j][e] = 1; // go to adjacent only when the // number of edges is more than 1 if (e > 1) { for ( int a = 0; a < V; a++) // adjacent of source i if (graph[i][a]) count[i][j][e] += count[a][j][e - 1]; } } } } return count[u][v][k]; } // driver program to test above function int main() { /* Let us create the graph shown in above diagram*/ int graph[V][V] = { { 0, 1, 1, 1 }, { 0, 0, 0, 1 }, { 0, 0, 0, 1 }, { 0, 0, 0, 0 } }; int u = 0, v = 3, k = 2; cout << countwalks(graph, u, v, k); return 0; } |
JAVA
// Java program to count walks from // u to v with exactly k edges import java.util.*; import java.lang.*; import java.io.*; class KPaths { static final int V = 4 ; // Number of vertices // A Dynamic programming based function to count walks from u // to v with k edges int countwalks( int graph[][], int u, int v, int k) { // Table to be filled up using DP. The value count[i][j][e] // will/ store count of possible walks from i to j with // exactly k edges int count[][][] = new int [V][V][k + 1 ]; // Loop for number of edges from 0 to k for ( int e = 0 ; e <= k; e++) { for ( int i = 0 ; i < V; i++) // for source { for ( int j = 0 ; j < V; j++) // for destination { // initialize value count[i][j][e] = 0 ; // from base cases if (e == 0 && i == j) count[i][j][e] = 1 ; if (e == 1 && graph[i][j] != 0 ) count[i][j][e] = 1 ; // go to adjacent only when number of edges // is more than 1 if (e > 1 ) { for ( int a = 0 ; a < V; a++) // adjacent of i if (graph[i][a] != 0 ) count[i][j][e] += count[a][j][e - 1 ]; } } } } return count[u][v][k]; } // Driver method public static void main(String[] args) throws java.lang.Exception { /* Let us create the graph shown in above diagram*/ int graph[][] = new int [][] { { 0 , 1 , 1 , 1 }, { 0 , 0 , 0 , 1 }, { 0 , 0 , 0 , 1 }, { 0 , 0 , 0 , 0 } }; int u = 0 , v = 3 , k = 2 ; KPaths p = new KPaths(); System.out.println(p.countwalks(graph, u, v, k)); } } // Contributed by Aakash Hasija |
Python3
# Python3 program to count walks from # u to v with exactly k edges # Number of vertices V = 4 # A Dynamic programming based function # to count walks from u to v with k edges def countwalks(graph, u, v, k): # Table to be filled up using DP. # The value count[i][j][e] will/ # store count of possible walks # from i to j with exactly k edges count = [[[ 0 for k in range (k + 1 )] for i in range (V)] for j in range (V)] # Loop for number of edges from 0 to k for e in range ( 0 , k + 1 ): # For Source for i in range (V): # For Destination for j in range (V): # Initialize value # count[i][j][e] = 0 # From base cases if (e = = 0 and i = = j): count[i][j][e] = 1 if (e = = 1 and graph[i][j] ! = 0 ): count[i][j][e] = 1 # Go to adjacent only when number # of edges is more than 1 if (e > 1 ): for a in range (V): # Adjacent of i if (graph[i][a] ! = 0 ): count[i][j][e] + = count[a][j][e - 1 ] return count[u][v][k] # Driver code if __name__ = = '__main__' : # Let us create the graph shown # in above diagram graph = [[ 0 , 1 , 1 , 1 ], [ 0 , 0 , 0 , 1 ], [ 0 , 0 , 0 , 1 ], [ 0 , 0 , 0 , 0 ]] u = 0 v = 3 k = 2 print (countwalks(graph, u, v, k)) # This code is contributed by Rajput-Ji |
C#
// C# program to count walks from u to v // with exactly k edges using System; class GFG { static int V = 4; // Number of vertices // A Dynamic programming based function // to count walks from u to v with k edges static int countwalks( int [, ] graph, int u, int v, int k) { // Table to be filled up using DP. The // value count[i][j][e] will/ store // count of possible walks from i to // j with exactly k edges int [,, ] count = new int [V, V, k + 1]; // Loop for number of edges from 0 to k for ( int e = 0; e <= k; e++) { // for source for ( int i = 0; i < V; i++) { // for destination for ( int j = 0; j < V; j++) { // initialize value count[i, j, e] = 0; // from base cases if (e == 0 && i == j) count[i, j, e] = 1; if (e == 1 && graph[i, j] != 0) count[i, j, e] = 1; // go to adjacent only when // number of edges // is more than 1 if (e > 1) { // adjacent of i for ( int a = 0; a < V; a++) if (graph[i, a] != 0) count[i, j, e] += count[a, j, e - 1]; } } } } return count[u, v, k]; } // Driver method public static void Main() { /* Let us create the graph shown in above diagram*/ int [, ] graph = { { 0, 1, 1, 1 }, { 0, 0, 0, 1 }, { 0, 0, 0, 1 }, { 0, 0, 0, 0 } }; int u = 0, v = 3, k = 2; Console.WriteLine( countwalks(graph, u, v, k)); } } // This is Code Contributed by anuj_67. |
Javascript
<script> // Javascript program to count walks from // u to v with exactly k edges // Number of vertices in the graph var V = 4 // A Dynamic programming based function to count walks from u // to v with k edges function countwalks(graph, u, v, k) { // Table to be filled up using DP. // The value count[i][j][e] will // store count of possible walks from // i to j with exactly k edges var count = new Array(V); for ( var i = 0; i <V; i++) { count[i] = new Array(V); for ( var j = 0; j < V; j++) { count[i][j] = new Array(V); for ( var e = 0; e <= k; e++) { count[i][j][e] = 0; } } } // Loop for number of edges from 0 to k for ( var e = 0; e <= k; e++) { for ( var i = 0; i < V; i++) // for source { for ( var j = 0; j < V; j++) // for destination { // initialize value count[i][j][e] = 0; // from base cases if (e == 0 && i == j) count[i][j][e] = 1; if (e == 1 && graph[i][j]) count[i][j][e] = 1; // go to adjacent only when the // number of edges is more than 1 if (e > 1) { for ( var a = 0; a < V; a++) // adjacent of source i if (graph[i][a]) count[i][j][e] += count[a][j][e - 1]; } } } } return count[u][v][k]; } // driver program to test above function /* Let us create the graph shown in above diagram*/ var graph = [ [ 0, 1, 1, 1 ], [ 0, 0, 0, 1 ], [ 0, 0, 0, 1 ], [ 0, 0, 0, 0 ] ]; var u = 0, v = 3, k = 2; document.write(countwalks(graph, u, v, k)); // This code is contributed by ShubhamSingh10 </script> |
输出:
2
复杂性分析:
- 时间复杂性: O(V) 3. ). 填充DP表需要三个嵌套循环,因此时间复杂度为O(V) 3/sup>)。
- 辅助空间: O(V) 3. ). 存储DP表O(V 3. )需要空间。
我们也可以使用 分而治之 在O(V)中解决上述问题 3. 时间到了。从u到v长度为k的行走计数是(图[v][v]中的第[u][v]项) K .我们可以通过使用 计算功率的分治技术 .两个大小为V x V的矩阵之间的乘法取O(V 3. )时间到了。 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



