有向无环图中的最长路径-yiteyi-C++库

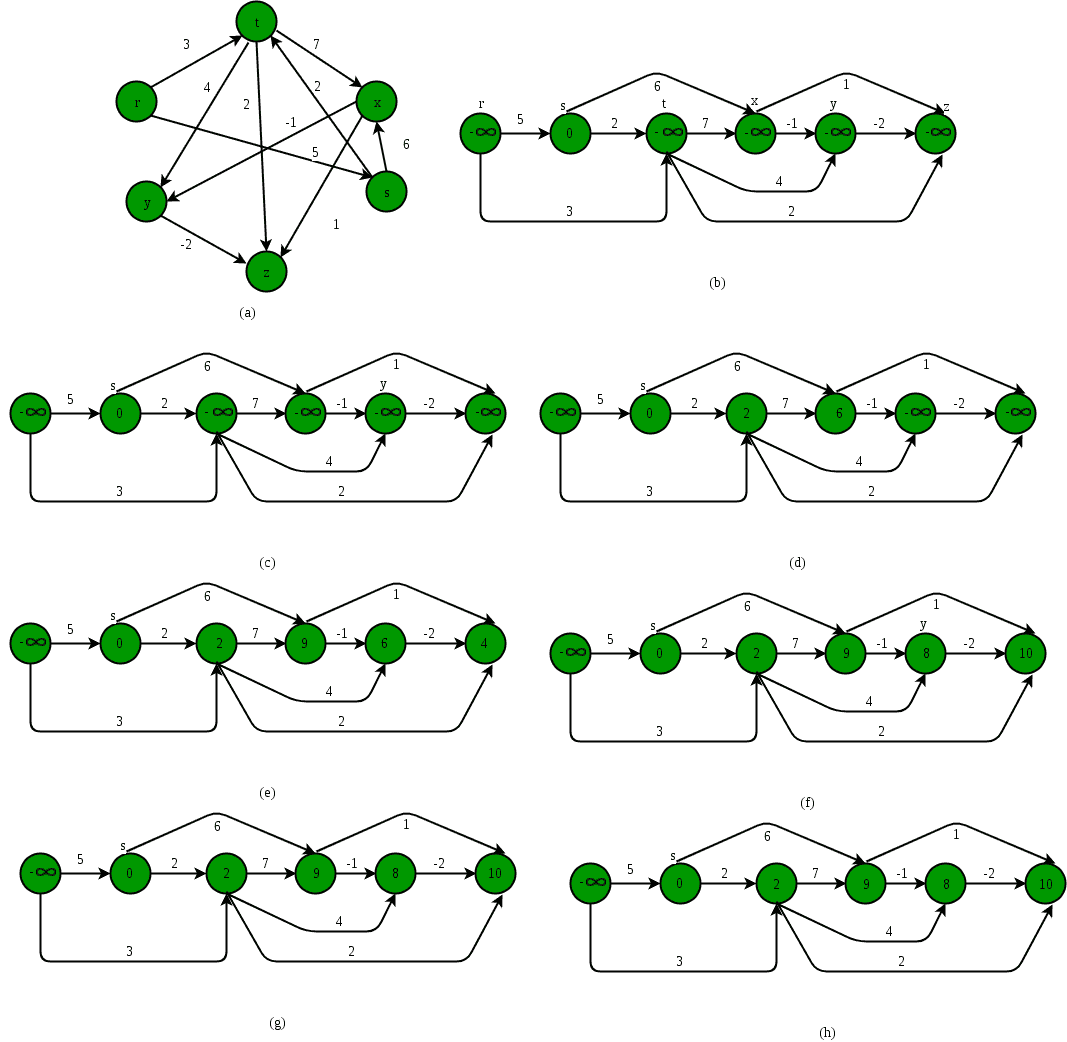
给一个加权的 D 定向的 A. 循环的 G 图（DAG）和其中的源顶点s，求从s到给定图中所有其他顶点的最长距离。一般图的最长路径问题不像最短路径问题那么简单，因为最长路径问题没有最优子结构性质事实上对于一般图，最长路径问题是NP难问题然而，对于有向无环图，最长路径问题有一个线性时间解。这个想法类似于有向无环图中最短路径的线性时间解。，我们使用拓扑排序 . 我们初始化到所有顶点的距离为负无穷大，到源的距离为0，然后我们找到一个拓扑排序这是图表的一部分。图的拓扑排序表示图的线性排序（参见下文，图（b）是图（a）的线性表示）。一旦我们有了拓扑顺序（或线性表示），我们就会按照拓扑顺序逐个处理所有顶点。对于正在处理的每个顶点，我们使用当前顶点的距离更新其相邻顶点的距离。下图显示了查找最长路径的逐步过程。

null

LongestPath

下面是寻找最长距离的完整算法。 1) 初始化dist[]={NINF，NINF，…}距离[s]=0，其中s是源顶点。这里NINF的意思是负无限。 2) 创建所有顶点的拓扑顺序。 3) 按拓扑顺序对每个顶点u执行以下操作。 ………..对u的每个相邻顶点v执行以下操作如果（距离[v] 距离[v]=距离[u]+重量（u，v）

下面是C++实现上述算法。

CPP

                         // A C++ program to find single source longest distances                       
                         // in a DAG                       
                         #include <iostream>                       
                         #include <limits.h>                       
                         #include <list>                       
                         #include <stack>                       
                         #define NINF INT_MIN                       
                         using                                     namespace                                     std;                       
           
                         // Graph is represented using adjacency list. Every                       
                         // node of adjacency list contains vertex number of                       
                         // the vertex to which edge connects. It also                       
                         // contains weight of the edge                       
                         class                                     AdjListNode {                       
                                                 int                                     v;                       
                                                 int                                     weight;                       
                                   
                         public                                     :                       
                                                 AdjListNode(                                     int                                     _v,                                     int                                     _w)                       
                                                 {                       
                                                 v = _v;                       
                                                 weight = _w;                       
                                                 }                       
                                                 int                                     getV() {                                     return                                     v; }                       
                                                 int                                     getWeight() {                                     return                                     weight; }                       
                         };                       
                                   
                         // Class to represent a graph using adjacency list                       
                         // representation                       
                         class                                     Graph {                       
                                                 int                                     V;                                     // No. of vertices'                       
                                   
                                                 // Pointer to an array containing adjacency lists                       
                                                 list<AdjListNode>* adj;                       
                                   
                                                 // A function used by longestPath                       
                                                 void                                     topologicalSortUtil(                                     int                                     v,                                     bool                                     visited[],                       
                                                 stack<                                     int                                     >& Stack);                       
                                   
                         public                                     :                       
                                                 Graph(                                     int                                     V);                                     // Constructor                       
                                                 ~Graph();                                     // Destructor                       
           
                                                 // function to add an edge to graph                       
                                                 void                                     addEdge(                                     int                                     u,                                     int                                     v,                                     int                                     weight);                       
                                   
                                                 // Finds longest distances from given source vertex                       
                                                 void                                     longestPath(                                     int                                     s);                       
                         };                       
                                   
                         Graph::Graph(                                     int                                     V)                                     // Constructor                       
                         {                       
                                                 this                                     ->V = V;                       
                                                 adj =                                     new                                     list<AdjListNode>[V];                       
                         }                       
           
                         Graph::~Graph()                                     // Destructor                       
                         {                       
                                                 delete                                     [] adj;                       
                         }                       
           
           
                         void                                     Graph::addEdge(                                     int                                     u,                                     int                                     v,                                     int                                     weight)                       
                         {                       
                                                 AdjListNode node(v, weight);                       
                                                 adj[u].push_back(node);                                     // Add v to u's list                       
                         }                       
                                   
                         // A recursive function used by longestPath. See below                       
                         // link for details                       
                         //                           https://                          www.geeksforgeeks.org/topological-sorting/                       
                         void                                     Graph::topologicalSortUtil(                                     int                                     v,                                     bool                                     visited[],                       
                                                 stack<                                     int                                     >& Stack)                       
                         {                       
                                                 // Mark the current node as visited                       
                                                 visited[v] =                                     true                                     ;                       
                                   
                                                 // Recur for all the vertices adjacent to this vertex                       
                                                 list<AdjListNode>::iterator i;                       
                                                 for                                     (i = adj[v].begin(); i != adj[v].end(); ++i) {                       
                                                 AdjListNode node = *i;                       
                                                 if                                     (!visited[node.getV()])                       
                                                 topologicalSortUtil(node.getV(), visited, Stack);                       
                                                 }                       
                                   
                                                 // Push current vertex to stack which stores topological                       
                                                 // sort                       
                                                 Stack.push(v);                       
                         }                       
                                   
                         // The function to find longest distances from a given vertex.                       
                         // It uses recursive topologicalSortUtil() to get topological                       
                         // sorting.                       
                         void                                     Graph::longestPath(                                     int                                     s)                       
                         {                       
                                                 stack<                                     int                                     > Stack;                       
                                                 int                                     dist[V];                       
                                   
                                                 // Mark all the vertices as not visited                       
                                                 bool                                     * visited =                                     new                                     bool                                     [V];                       
                                                 for                                     (                                     int                                     i = 0; i < V; i++)                       
                                                 visited[i] =                                     false                                     ;                       
                                   
                                                 // Call the recursive helper function to store Topological                       
                                                 // Sort starting from all vertices one by one                       
                                                 for                                     (                                     int                                     i = 0; i < V; i++)                       
                                                 if                                     (visited[i] ==                                     false                                     )                       
                                                 topologicalSortUtil(i, visited, Stack);                       
                                   
                                                 // Initialize distances to all vertices as infinite and                       
                                                 // distance to source as 0                       
                                                 for                                     (                                     int                                     i = 0; i < V; i++)                       
                                                 dist[i] = NINF;                       
                                                 dist[s] = 0;                       
                                                 // Process vertices in topological order                       
                                                 while                                     (Stack.empty() ==                                     false                                     ) {                       
                                                 // Get the next vertex from topological order                       
                                                 int                                     u = Stack.top();                       
                                                 Stack.pop();                       
                                   
                                                 // Update distances of all adjacent vertices                       
                                                 list<AdjListNode>::iterator i;                       
                                                 if                                     (dist[u] != NINF) {                       
                                                 for                                     (i = adj[u].begin(); i != adj[u].end(); ++i){                       
                                   
                                                 if                                     (dist[i->getV()] < dist[u] + i->getWeight())                       
                                                 dist[i->getV()] = dist[u] + i->getWeight();                       
                                                 }                       
                                                 }                       
                                                 }                       
                                   
                                                 // Print the calculated longest distances                       
                                                 for                                     (                                     int                                     i = 0; i < V; i++)                       
                                                 (dist[i] == NINF) ? cout <<                                     "INF "                                     : cout << dist[i] <<                                     " "                                     ;                       
                                   
                                                 delete                                     [] visited;                       
                         }                       
                                   
                         // Driver program to test above functions                       
                         int                                     main()                       
                         {                       
                                                 // Create a graph given in the above diagram.                       
                                                 // Here vertex numbers are 0, 1, 2, 3, 4, 5 with                       
                                                 // following mappings:                       
                                                 // 0=r, 1=s, 2=t, 3=x, 4=y, 5=z                       
                                                 Graph g(6);                       
                                                 g.addEdge(0, 1, 5);                       
                                                 g.addEdge(0, 2, 3);                       
                                                 g.addEdge(1, 3, 6);                       
                                                 g.addEdge(1, 2, 2);                       
                                                 g.addEdge(2, 4, 4);                       
                                                 g.addEdge(2, 5, 2);                       
                                                 g.addEdge(2, 3, 7);                       
                                                 g.addEdge(3, 5, 1);                       
                                                 g.addEdge(3, 4, -1);                       
                                                 g.addEdge(4, 5, -2);                       
                                   
                                                 int                                     s = 1;                       
                                                 cout <<                                     "Following are longest distances from "                       
                                                 "source vertex "                       
                                                 << s <<                                     " "                                     ;                       
                                                 g.longestPath(s);                       
                                   
                                                 return                                     0;                       
                         }                       

JAVA

                         // A Java program to find single source longest distances                       
                         // in a DAG                       
                         import                                     java.util.*;                       
                         class                                     GFG                       
                         {                       
                                   
                                                 // Graph is represented using adjacency list. Every                       
                                                 // node of adjacency list contains vertex number of                       
                                                 // the vertex to which edge connects. It also                       
                                                 // contains weight of the edge                       
                                                 static                                     class                                     AdjListNode {                       
                                                 int                                     v;                       
                                                 int                                     weight;                       
           
                                                 AdjListNode(                                     int                                     _v,                                     int                                     _w)                       
                                                 {                       
                                                 v = _v;                       
                                                 weight = _w;                       
                                                 }                       
                                                 int                                     getV() {                                     return                                     v; }                       
                                                 int                                     getWeight() {                                     return                                     weight; }                       
                                                 }                       
           
                                                 // Class to represent a graph using adjacency list                       
                                                 // representation                       
                                                 static                                     class                                     Graph {                       
                                                 int                                     V;                                     // No. of vertices'                       
           
                                                 // Pointer to an array containing adjacency lists                       
                                                 ArrayList<ArrayList<AdjListNode>> adj;                       
           
                                                 Graph(                                     int                                     V)                                     // Constructor                       
                                                 {                       
                                                 this                                     .V = V;                       
                                                 adj =                                     new                                     ArrayList<ArrayList<AdjListNode>>(V);                       
           
                                                 for                                     (                                     int                                     i =                                     0                                     ; i < V; i++){                       
                                                 adj.add(                                     new                                     ArrayList<AdjListNode>());                       
                                                 }                       
                                                 }                       
           
                                                 void                                     addEdge(                                     int                                     u,                                     int                                     v,                                     int                                     weight)                       
                                                 {                       
                                                 AdjListNode node =                                     new                                     AdjListNode(v, weight);                       
                                                 adj.get(u).add(node);                                     // Add v to u's list                       
                                                 }                       
           
                                                 // A recursive function used by longestPath. See below                       
                                                 // link for details                       
                                                 //                           https://                          www.geeksforgeeks.org/topological-sorting/                       
                                                 void                                     topologicalSortUtil(                                     int                                     v,                                     boolean                                     visited[],                       
                                                 Stack<Integer> stack)                       
                                                 {                       
                                                 // Mark the current node as visited                       
                                                 visited[v] =                                     true                                     ;                       
           
                                                 // Recur for all the vertices adjacent to this vertex                       
                                                 for                                     (                                     int                                     i =                                     0                                     ; i<adj.get(v).size(); i++) {                       
                                                 AdjListNode node = adj.get(v).get(i);                       
                                                 if                                     (!visited[node.getV()])                       
                                                 topologicalSortUtil(node.getV(), visited, stack);                       
                                                 }                       
           
                                                 // Push current vertex to stack which stores topological                       
                                                 // sort                       
                                                 stack.push(v);                       
                                                 }                       
           
                                                 // The function to find longest distances from a given vertex.                       
                                                 // It uses recursive topologicalSortUtil() to get topological                       
                                                 // sorting.                       
                                                 void                                     longestPath(                                     int                                     s)                       
                                                 {                       
                                                 Stack<Integer> stack =                                     new                                     Stack<Integer>();                       
                                                 int                                     dist[] =                                     new                                     int                                     [V];                       
           
                                                 // Mark all the vertices as not visited                       
                                                 boolean                                     visited[] =                                     new                                     boolean                                     [V];                       
                                                 for                                     (                                     int                                     i =                                     0                                     ; i < V; i++)                       
                                                 visited[i] =                                     false                                     ;                       
           
                                                 // Call the recursive helper function to store Topological                       
                                                 // Sort starting from all vertices one by one                       
                                                 for                                     (                                     int                                     i =                                     0                                     ; i < V; i++)                       
                                                 if                                     (visited[i] ==                                     false                                     )                       
                                                 topologicalSortUtil(i, visited, stack);                       
           
                                                 // Initialize distances to all vertices as infinite and                       
                                                 // distance to source as 0                       
                                                 for                                     (                                     int                                     i =                                     0                                     ; i < V; i++)                       
                                                 dist[i] = Integer.MIN_VALUE;                       
           
                                                 dist[s] =                                     0                                     ;                       
                                   
                                                 // Process vertices in topological order                       
                                                 while                                     (stack.isEmpty() ==                                     false                                     )                       
                                                 {                       
                                   
                                                 // Get the next vertex from topological order                       
                                                 int                                     u = stack.peek();                       
                                                 stack.pop();                       
           
                                                 // Update distances of all adjacent vertices ;                       
                                                 if                                     (dist[u] != Integer.MIN_VALUE)                       
                                                 {                       
                                                 for                                     (                                     int                                     i =                                     0                                     ; i<adj.get(u).size(); i++)                       
                                                 {                       
                                                 AdjListNode node = adj.get(u).get(i);                       
                                                 if                                     (dist[node.getV()] < dist[u] + node.getWeight())                       
                                                 dist[node.getV()] = dist[u] + node.getWeight();                       
                                                 }                       
                                                 }                       
                                                 }                       
           
                                                 // Print the calculated longest distances                       
                                                 for                                     (                                     int                                     i =                                     0                                     ; i < V; i++)                       
                                                 if                                     (dist[i] == Integer.MIN_VALUE)                       
                                                 System.out.print(                                     "INF "                                     );                       
                                                 else                       
                                                 System.out.print(dist[i] +                                     " "                                     );                       
                                                 }                       
                                                 }                       
           
                                                 // Driver program to test above functions                       
                                                 public                                     static                                     void                                     main(String args[])                       
                                                 {                       
                                                 // Create a graph given in the above diagram.                       
                                                 // Here vertex numbers are 0, 1, 2, 3, 4, 5 with                       
                                                 // following mappings:                       
                                                 // 0=r, 1=s, 2=t, 3=x, 4=y, 5=z                       
                                                 Graph g =                                     new                                     Graph(                                     6                                     );                       
                                                 g.addEdge(                                     0                                     ,                                     1                                     ,                                     5                                     );                       
                                                 g.addEdge(                                     0                                     ,                                     2                                     ,                                     3                                     );                       
                                                 g.addEdge(                                     1                                     ,                                     3                                     ,                                     6                                     );                       
                                                 g.addEdge(                                     1                                     ,                                     2                                     ,                                     2                                     );                       
                                                 g.addEdge(                                     2                                     ,                                     4                                     ,                                     4                                     );                       
                                                 g.addEdge(                                     2                                     ,                                     5                                     ,                                     2                                     );                       
                                                 g.addEdge(                                     2                                     ,                                     3                                     ,                                     7                                     );                       
                                                 g.addEdge(                                     3                                     ,                                     5                                     ,                                     1                                     );                       
                                                 g.addEdge(                                     3                                     ,                                     4                                     , -                                     1                                     );                       
                                                 g.addEdge(                                     4                                     ,                                     5                                     , -                                     2                                     );                       
           
                                                 int                                     s =                                     1                                     ;                       
                                                 System.out.print(                                     "Following are longest distances from source vertex "                                     + s +                                     " "                                     );                       
                                                 g.longestPath(s);                       
           
                                                 }                       
                         }                       
           
                         // This code is contribute by adityapande88.                       

Python3

                         # A recursive function used by longestPath. See below                       
                         # link for details                       
                         # https:#www.geeksforgeeks.org/topological-sorting/                       
                         def                                     topologicalSortUtil(v):                       
                                                 global                                     Stack, visited, adj                       
                                                 visited[v]                                     =                                     True                       
           
                                                 # Recur for all the vertices adjacent to this vertex                       
                                                 # list<AdjListNode>::iterator i                       
                                                 for                                     i                                     in                                     adj[v]:                       
                                                 if                                     (                                     not                                     visited[i[                                     0                                     ]]):                       
                                                 topologicalSortUtil(i[                                     0                                     ])                       
           
                                                 # Push current vertex to stack which stores topological                       
                                                 # sort                       
                                                 Stack.append(v)                       
           
                         # The function to find longest distances from a given vertex.                       
                         # It uses recursive topologicalSortUtil() to get topological                       
                         # sorting.                       
                         def                                     longestPath(s):                       
                                                 global                                     Stack, visited, adj, V                       
                                                 dist                                     =                                     [                                     -                                     10                                     *                                     *                                     9                                     for                                     i                                     in                                     range                                     (V)]                       
           
                                                 # Call the recursive helper function to store Topological                       
                                                 # Sort starting from all vertices one by one                       
                                                 for                                     i                                     in                                     range                                     (V):                       
                                                 if                                     (visited[i]                                     =                                     =                                     False                                     ):                       
                                                 topologicalSortUtil(i)                       
                                                 # print(Stack)                       
           
                                                 # Initialize distances to all vertices as infinite and                       
                                                 # distance to source as 0                       
                                                 dist[s]                                     =                                     0                       
                                                 # Stack.append(1)                       
           
                                                 # Process vertices in topological order                       
                                                 while                                     (                                     len                                     (Stack) >                                     0                                     ):                       
                                   
                                                 # Get the next vertex from topological order                       
                                                 u                                     =                                     Stack[                                     -                                     1                                     ]                       
                                                 del                                     Stack[                                     -                                     1                                     ]                       
                                                 #print(u)                       
           
                                                 # Update distances of all adjacent vertices                       
                                                 # list<AdjListNode>::iterator i                       
                                                 if                                     (dist[u] !                                     =                                     10                                     *                                     *                                     9                                     ):                       
                                                 for                                     i                                     in                                     adj[u]:                       
                                                 # print(u, i)                       
                                                 if                                     (dist[i[                                     0                                     ]] < dist[u]                                     +                                     i[                                     1                                     ]):                       
                                                 dist[i[                                     0                                     ]]                                     =                                     dist[u]                                     +                                     i[                                     1                                     ]                       
           
                                                 # Print calculated longest distances                       
                                                 # print(dist)                       
                                                 for                                     i                                     in                                     range                                     (V):                       
                                                 print                                     (                                     "INF "                                     ,end                                     =                                     "                                     ") if (dist[i] == -10**9) else print(dist[i],end="                                     ")                       
           
                         # Driver code                       
                         if                                     __name__                                     =                                     =                                     '__main__'                                     :                       
                                                 V, Stack, visited                                     =                                     6                                     , [], [                                     False                                     for                                     i                                     in                                     range                                     (                                     7                                     )]                       
                                                 adj                                     =                                     [[]                                     for                                     i                                     in                                     range                                     (                                     7                                     )]                       
                                   
                                                 # Create a graph given in the above diagram.                       
                                                 # Here vertex numbers are 0, 1, 2, 3, 4, 5 with                       
                                                 # following mappings:                       
                                                 # 0=r, 1=s, 2=t, 3=x, 4=y, 5=z                       
                                                 adj[                                     0                                     ].append([                                     1                                     ,                                     5                                     ])                       
                                                 adj[                                     0                                     ].append([                                     2                                     ,                                     3                                     ])                       
                                                 adj[                                     1                                     ].append([                                     3                                     ,                                     6                                     ])                       
                                                 adj[                                     1                                     ].append([                                     2                                     ,                                     2                                     ])                       
                                                 adj[                                     2                                     ].append([                                     4                                     ,                                     4                                     ])                       
                                                 adj[                                     2                                     ].append([                                     5                                     ,                                     2                                     ])                       
                                                 adj[                                     2                                     ].append([                                     3                                     ,                                     7                                     ])                       
                                                 adj[                                     3                                     ].append([                                     5                                     ,                                     1                                     ])                       
                                                 adj[                                     3                                     ].append([                                     4                                     ,                                     -                                     1                                     ])                       
                                                 adj[                                     4                                     ].append([                                     5                                     ,                                     -                                     2                                     ])                       
           
                                                 s                                     =                                     1                       
                                                 print                                     (                                     "Following are longest distances from source vertex "                                     ,s)                       
                                                 longestPath(s)                       
           
                                                 # This code is contributed by mohit kumar 29.                       

输出：

Following are longest distances from source vertex 1INF 0 2 9 8 10

时间复杂性： 拓扑排序的时间复杂度为O（V+E）。在找到拓扑顺序后，该算法处理所有顶点，并对每个顶点对所有相邻顶点进行循环。图中的所有相邻顶点都是O（E）。所以内部循环运行O（V+E）次。因此，该算法的总体时间复杂度为O（V+E）。 练习： 上述解决方案可以打印最长距离，还可以将代码扩展到打印路径。

微焦点

如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写评论

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章