给定大小为n的排序数组arr[]和要在其中搜索的元素x。返回x的索引,如果它存在于数组中,则返回-1。 例如:
Input: arr[] = {2, 3, 4, 10, 40}, x = 10Output: 3Element x is present at index 3.Input: arr[] = {2, 3, 4, 10, 40}, x = 11Output: -1Element x is not present.
斐波那契搜索是一种基于比较的技术,它使用斐波那契数来搜索排序数组中的元素。 与二进制搜索的相似之处:
- 适用于排序数组
- 分治算法。
- 具有对数n时间复杂性。
与二进制搜索的区别 :
- 斐波那契搜索将给定数组分成不相等的部分
- 二进制搜索使用除法运算符来划分范围。斐波那契搜索不使用/,而是使用+和-。除法运算符在某些CPU上的成本可能很高。
- 斐波那契搜索在随后的步骤中检查相对较近的元素。因此,当输入数组太大,无法放入CPU缓存甚至RAM时,斐波那契搜索可能会很有用。
背景: 斐波那契数递归定义为F(n)=F(n-1)+F(n-2),F(0)=0,F(1)=1。前几个斐波那契数是0,1,1,2,3,5,8,13,21,34,55,89,144… 观察: 下面的观测用于距离消除,因此用于O(log(n))复杂度。
F(n - 2) ≈ (1/3)*F(n) and F(n - 1) ≈ (2/3)*F(n).
算法: 让搜索的元素为x。 其思想是首先找到大于或等于给定数组长度的最小斐波那契数。让找到的斐波那契数为fib(第m个斐波那契数)。我们使用(m-2)的第th斐波那契数作为索引(如果它是有效的索引)。设(m-2)的第个斐波那契数为i,我们比较arr[i]和x,如果x相同,我们返回i。否则如果x更大,我们在i之后的子数组中重复,否则在i之前的子数组中重复。 下面是完整的算法 设arr[0..n-1]为输入数组,要搜索的元素为x。
- 找到大于或等于n的最小斐波那契数。让这个数为fibM[m’th Fibonacci Number]。让它前面的两个斐波那契数分别是fibMm1[(m-1)第个斐波那契数]和fibMm2[(m-2)第个斐波那契数]。
- 当阵列中有要检查的元素时:
- 将x与fibMm2覆盖范围内的最后一个元素进行比较
- 如果 x匹配,返回索引
- 否则如果 x小于元素,将三个斐波那契变量向下移动两个斐波那契,表示消除了剩余数组的大约三分之二。
- 其他的 x大于元素,将三个斐波那契变量向下移动一个斐波那契。将偏移量重置为索引。这些因素加在一起表明,剩余阵列的大约三分之一被消除。
- 由于可能还有一个元素可供比较,请检查fibMm1是否为1。如果是,将x与剩余元素进行比较。如果匹配,则返回索引。
C
// C program for Fibonacci Search #include <stdio.h> // Utility function to find minimum of two elements int min( int x, int y) { return (x <= y) ? x : y; } /* Returns index of x if present, else returns -1 */ int fibMonaccianSearch( int arr[], int x, int n) { /* Initialize fibonacci numbers */ int fibMMm2 = 0; // (m-2)'th Fibonacci No. int fibMMm1 = 1; // (m-1)'th Fibonacci No. int fibM = fibMMm2 + fibMMm1; // m'th Fibonacci /* fibM is going to store the smallest Fibonacci Number greater than or equal to n */ while (fibM < n) { fibMMm2 = fibMMm1; fibMMm1 = fibM; fibM = fibMMm2 + fibMMm1; } // Marks the eliminated range from front int offset = -1; /* while there are elements to be inspected. Note that we compare arr[fibMm2] with x. When fibM becomes 1, fibMm2 becomes 0 */ while (fibM > 1) { // Check if fibMm2 is a valid location int i = min(offset + fibMMm2, n - 1); /* If x is greater than the value at index fibMm2, cut the subarray array from offset to i */ if (arr[i] < x) { fibM = fibMMm1; fibMMm1 = fibMMm2; fibMMm2 = fibM - fibMMm1; offset = i; } /* If x is greater than the value at index fibMm2, cut the subarray after i+1 */ else if (arr[i] > x) { fibM = fibMMm2; fibMMm1 = fibMMm1 - fibMMm2; fibMMm2 = fibM - fibMMm1; } /* element found. return index */ else return i; } /* comparing the last element with x */ if (fibMMm1 && arr[offset + 1] == x) return offset + 1; /*element not found. return -1 */ return -1; } /* driver function */ int main( void ) { int arr[] = { 10, 22, 35, 40, 45, 50, 80, 82, 85, 90, 100,235}; int n = sizeof (arr) / sizeof (arr[0]); int x = 235; int ind = fibMonaccianSearch(arr, x, n); if (ind>=0) printf ( "Found at index: %d" ,ind); else printf ( "%d isn't present in the array" ,x); return 0; } |
JAVA
// Java program for Fibonacci Search import java.util.*; class Fibonacci { // Utility function to find minimum // of two elements public static int min( int x, int y) { return (x <= y) ? x : y; } /* Returns index of x if present, else returns -1 */ public static int fibMonaccianSearch( int arr[], int x, int n) { /* Initialize fibonacci numbers */ int fibMMm2 = 0 ; // (m-2)'th Fibonacci No. int fibMMm1 = 1 ; // (m-1)'th Fibonacci No. int fibM = fibMMm2 + fibMMm1; // m'th Fibonacci /* fibM is going to store the smallest Fibonacci Number greater than or equal to n */ while (fibM < n) { fibMMm2 = fibMMm1; fibMMm1 = fibM; fibM = fibMMm2 + fibMMm1; } // Marks the eliminated range from front int offset = - 1 ; /* while there are elements to be inspected. Note that we compare arr[fibMm2] with x. When fibM becomes 1, fibMm2 becomes 0 */ while (fibM > 1 ) { // Check if fibMm2 is a valid location int i = min(offset + fibMMm2, n - 1 ); /* If x is greater than the value at index fibMm2, cut the subarray array from offset to i */ if (arr[i] < x) { fibM = fibMMm1; fibMMm1 = fibMMm2; fibMMm2 = fibM - fibMMm1; offset = i; } /* If x is less than the value at index fibMm2, cut the subarray after i+1 */ else if (arr[i] > x) { fibM = fibMMm2; fibMMm1 = fibMMm1 - fibMMm2; fibMMm2 = fibM - fibMMm1; } /* element found. return index */ else return i; } /* comparing the last element with x */ if (fibMMm1 == 1 && arr[n- 1 ] == x) return n- 1 ; /*element not found. return -1 */ return - 1 ; } // driver code public static void main(String[] args) { int arr[] = { 10 , 22 , 35 , 40 , 45 , 50 , 80 , 82 , 85 , 90 , 100 , 235 }; int n = 12 ; int x = 235 ; int ind = fibMonaccianSearch(arr, x, n); if (ind>= 0 ) System.out.print( "Found at index: " +ind); else System.out.print(x+ " isn't present in the array" ); } } // This code is contributed by rishabh_jain |
Python3
# Python3 program for Fibonacci search. from bisect import bisect_left # Returns index of x if present, else # returns -1 def fibMonaccianSearch(arr, x, n): # Initialize fibonacci numbers fibMMm2 = 0 # (m-2)'th Fibonacci No. fibMMm1 = 1 # (m-1)'th Fibonacci No. fibM = fibMMm2 + fibMMm1 # m'th Fibonacci # fibM is going to store the smallest # Fibonacci Number greater than or equal to n while (fibM < n): fibMMm2 = fibMMm1 fibMMm1 = fibM fibM = fibMMm2 + fibMMm1 # Marks the eliminated range from front offset = - 1 # while there are elements to be inspected. # Note that we compare arr[fibMm2] with x. # When fibM becomes 1, fibMm2 becomes 0 while (fibM > 1 ): # Check if fibMm2 is a valid location i = min (offset + fibMMm2, n - 1 ) # If x is greater than the value at # index fibMm2, cut the subarray array # from offset to i if (arr[i] < x): fibM = fibMMm1 fibMMm1 = fibMMm2 fibMMm2 = fibM - fibMMm1 offset = i # If x is less than the value at # index fibMm2, cut the subarray # after i+1 elif (arr[i] > x): fibM = fibMMm2 fibMMm1 = fibMMm1 - fibMMm2 fibMMm2 = fibM - fibMMm1 # element found. return index else : return i # comparing the last element with x */ if (fibMMm1 and arr[n - 1 ] = = x): return n - 1 # element not found. return -1 return - 1 # Driver Code arr = [ 10 , 22 , 35 , 40 , 45 , 50 , 80 , 82 , 85 , 90 , 100 , 235 ] n = len (arr) x = 235 ind = fibMonaccianSearch(arr, x, n) if ind> = 0 : print ( "Found at index:" ,ind) else : print (x, "isn't present in the array" ); # This code is contributed by rishabh_jain |
C#
// C# program for Fibonacci Search using System; class GFG { // Utility function to find minimum // of two elements public static int min( int x, int y) { return (x <= y) ? x : y; } /* Returns index of x if present, else returns -1 */ public static int fibMonaccianSearch( int [] arr, int x, int n) { /* Initialize fibonacci numbers */ int fibMMm2 = 0; // (m-2)'th Fibonacci No. int fibMMm1 = 1; // (m-1)'th Fibonacci No. int fibM = fibMMm2 + fibMMm1; // m'th Fibonacci /* fibM is going to store the smallest Fibonacci Number greater than or equal to n */ while (fibM < n) { fibMMm2 = fibMMm1; fibMMm1 = fibM; fibM = fibMMm2 + fibMMm1; } // Marks the eliminated range from front int offset = -1; /* while there are elements to be inspected. Note that we compare arr[fibMm2] with x. When fibM becomes 1, fibMm2 becomes 0 */ while (fibM > 1) { // Check if fibMm2 is a valid location int i = min(offset + fibMMm2, n - 1); /* If x is greater than the value at index fibMm2, cut the subarray array from offset to i */ if (arr[i] < x) { fibM = fibMMm1; fibMMm1 = fibMMm2; fibMMm2 = fibM - fibMMm1; offset = i; } /* If x is less than the value at index fibMm2, cut the subarray after i+1 */ else if (arr[i] > x) { fibM = fibMMm2; fibMMm1 = fibMMm1 - fibMMm2; fibMMm2 = fibM - fibMMm1; } /* element found. return index */ else return i; } /* comparing the last element with x */ if (fibMMm1 == 1 && arr[n-1] == x) return n-1; /*element not found. return -1 */ return -1; } // driver code public static void Main() { int [] arr = { 10, 22, 35, 40, 45, 50, 80, 82, 85, 90, 100,235 }; int n = 12; int x = 235; int ind = fibMonaccianSearch(arr, x, n); if (ind>=0) Console.Write( "Found at index: " +ind); else Console.Write(x+ " isn't present in the array" ); } } // This code is contributed by nitin mittal. |
PHP
<?php // PHP program for Fibonacci Search /* Returns index of x if present, else returns -1 */ function fibMonaccianSearch( $arr , $x , $n ) { /* Initialize fibonacci numbers */ $fibMMm2 = 0; // (m-2)'th Fibonacci No. $fibMMm1 = 1; // (m-1)'th Fibonacci No. $fibM = $fibMMm2 + $fibMMm1 ; // m'th Fibonacci /* fibM is going to store the smallest Fibonacci Number greater than or equal to n */ while ( $fibM < $n ) { $fibMMm2 = $fibMMm1 ; $fibMMm1 = $fibM ; $fibM = $fibMMm2 + $fibMMm1 ; } // Marks the eliminated range from front $offset = -1; /* while there are elements to be inspected. Note that we compare arr[fibMm2] with x. When fibM becomes 1, fibMm2 becomes 0 */ while ( $fibM > 1) { // Check if fibMm2 is a valid location $i = min( $offset + $fibMMm2 , $n -1); /* If x is greater than the value at index fibMm2, cut the subarray array from offset to i */ if ( $arr [ $i ] < $x ) { $fibM = $fibMMm1 ; $fibMMm1 = $fibMMm2 ; $fibMMm2 = $fibM - $fibMMm1 ; $offset = $i ; } /* If x is less than the value at index fibMm2, cut the subarray after i+1 */ else if ( $arr [ $i ] > $x ) { $fibM = $fibMMm2 ; $fibMMm1 = $fibMMm1 - $fibMMm2 ; $fibMMm2 = $fibM - $fibMMm1 ; } /* element found. return index */ else return $i ; } /* comparing the last element with x */ if ( $fibMMm1 && $arr [ $n -1] == $x ) return $n -1; /*element not found. return -1 */ return -1; } /* driver code */ $arr = array (10, 22, 35, 40, 45, 50, 80, 82,85, 90, 100,235); $n = count ( $arr ); $x = 235; $ind = fibMonaccianSearch( $arr , $x , $n ); if ( $ind >=0) printf( "Found at index: " . $ind ); else printf( $x . " isn't present in the array" ); // This code is contributed by mits ?> |
Javascript
<script> // Javascript program for Fibonacci Search /* Returns index of x if present, else returns -1 */ function fibMonaccianSearch(arr, x, n) { /* Initialize fibonacci numbers */ let fibMMm2 = 0; // (m-2)'th Fibonacci No. let fibMMm1 = 1; // (m-1)'th Fibonacci No. let fibM = fibMMm2 + fibMMm1; // m'th Fibonacci /* fibM is going to store the smallest Fibonacci Number greater than or equal to n */ while (fibM < n) { fibMMm2 = fibMMm1; fibMMm1 = fibM; fibM = fibMMm2 + fibMMm1; } // Marks the eliminated range from front let offset = -1; /* while there are elements to be inspected. Note that we compare arr[fibMm2] with x. When fibM becomes 1, fibMm2 becomes 0 */ while (fibM > 1) { // Check if fibMm2 is a valid location let i = Math.min(offset + fibMMm2, n-1); /* If x is greater than the value at index fibMm2, cut the subarray array from offset to i */ if (arr[i] < x) { fibM = fibMMm1; fibMMm1 = fibMMm2; fibMMm2 = fibM - fibMMm1; offset = i; } /* If x is less than the value at index fibMm2, cut the subarray after i+1 */ else if (arr[i] > x) { fibM = fibMMm2; fibMMm1 = fibMMm1 - fibMMm2; fibMMm2 = fibM - fibMMm1; } /* element found. return index */ else return i; } /* comparing the last element with x */ if (fibMMm1 && arr[n-1] == x){ return n-1 } /*element not found. return -1 */ return -1; } /* driver code */ let arr = [10, 22, 35, 40, 45, 50, 80, 82,85, 90, 100,235]; let n = arr.length; let x = 235; let ind = fibMonaccianSearch(arr, x, n); if (ind>=0){ document.write( "Found at index: " + ind); } else { document.write(x + " isn't present in the array" ); } // This code is contributed by _saurabh_jaiswal </script> |
Found at index: 11
插图: 让我们用下面的例子来理解算法:

插图假设:基于1的索引。目标元素x是85。数组的长度n=11。 大于或等于11的最小斐波那契数是13。如图所示,fibMm2=5,fibMm1=8,fibM=13。 另一个实现细节是偏移量变量(初始化为零)。它从前面开始标记已消除的范围。我们会不时更新。 现在,由于偏移值是一个索引,包括它和它以下的所有索引都已被删除,所以只需要添加一些内容。由于fibMm2标记了我们数组的大约三分之一,以及它标记的索引,因此我们可以将fibMm2添加到偏移量中,并在索引i=min(偏移量+fibMm2,n)处检查元素。

可视化:
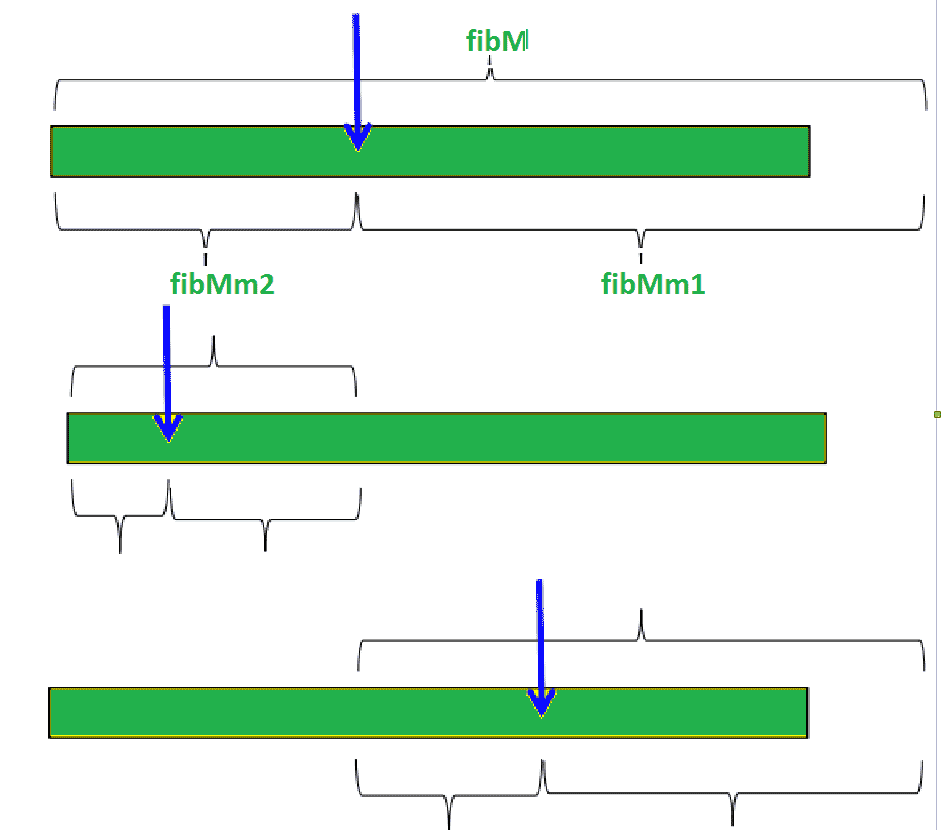
时间复杂性分析: 最坏的情况是,当我们继续寻找目标时,目标位于阵列的较大部分(2/3)。换句话说,我们每次都要消除数组中较小的部分(1/3)。我们一次调用n,然后调用(2/3)n,然后调用(4/9)n,从今往后。 认为:
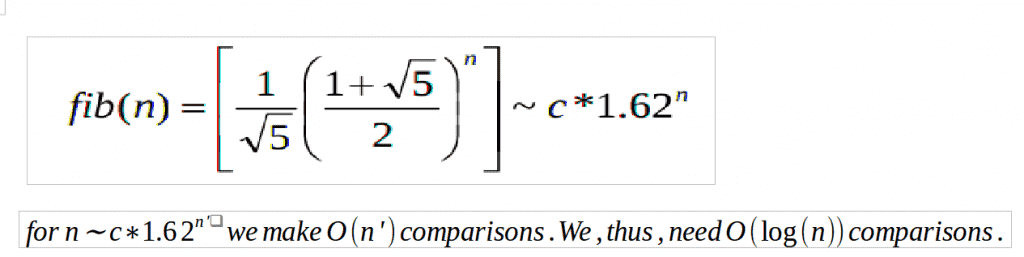
参考资料: https://en.wikipedia.org/wiki/Fibonacci_search_technique 本文由 亚什·瓦里亚尼 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



