给定一棵树,其中每个节点都包含可变数量的子节点,请将该树转换为其镜像。下图显示了一个示例。
null
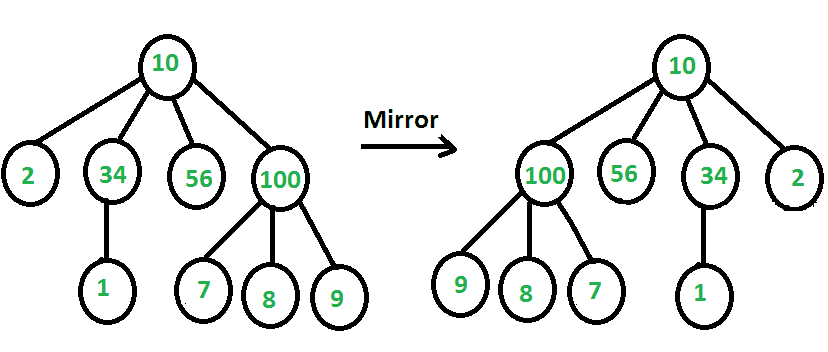
我们强烈建议您尽量减少浏览器,并先自己尝试。 树的节点表示为一个键和一个大小可变的子指针数组。这个想法类似于二叉树的镜像。对于每个节点,我们首先对其所有子节点重复,然后反转子节点指针数组。我们也可以用另一种方式来完成这些步骤,即首先反转子指针数组,然后针对子指针重复执行这些步骤。 下面是C++实现上述思想。
C++
// C++ program to mirror an n-ary tree #include <bits/stdc++.h> using namespace std; // Represents a node of an n-ary tree struct Node { int key; vector<Node *>child; }; // Function to convert a tree to its mirror void mirrorTree(Node * root) { // Base case: Nothing to do if root is NULL if (root==NULL) return ; // Number of children of root int n = root->child.size(); // If number of child is less than 2 i.e. // 0 or 1 we do not need to do anything if (n < 2) return ; // Calling mirror function for each child for ( int i=0; i<n; i++) mirrorTree(root->child[i]); // Reverse vector (variable sized array) of child // pointers reverse(root->child.begin(), root->child.end()); } // Utility function to create a new tree node Node *newNode( int key) { Node *temp = new Node; temp->key = key; return temp; } // Prints the n-ary tree level wise void printNodeLevelWise(Node * root) { if (root==NULL) return ; // Create a queue and enqueue root to it queue<Node *>q; q.push(root); // Do level order traversal. Two loops are used // to make sure that different levels are printed // in different lines while (!q.empty()) { int n = q.size(); while (n>0) { // Dequeue an item from queue and print it Node * p = q.front(); q.pop(); cout << p->key << " " ; // Enqueue all childrent of the dequeued item for ( int i=0; i<p->child.size(); i++) q.push(p->child[i]); n--; } cout << endl; // Separator between levels } } // Driver program int main() { /* Let us create below tree * 10 * / / * 2 34 56 100 * | / | * 1 7 8 9 */ Node *root = newNode(10); (root->child).push_back(newNode(2)); (root->child).push_back(newNode(34)); (root->child).push_back(newNode(56)); (root->child).push_back(newNode(100)); (root->child[2]->child).push_back(newNode(1)); (root->child[3]->child).push_back(newNode(7)); (root->child[3]->child).push_back(newNode(8)); (root->child[3]->child).push_back(newNode(9)); cout << "Level order traversal Before Mirroring" ; printNodeLevelWise(root); mirrorTree(root); cout << "Level order traversal After Mirroring" ; printNodeLevelWise(root); return 0; } |
Python3
# Python program to mirror an n-ary tree # Represents a node of an n-ary tree class Node : # Utility function to create a new tree node def __init__( self ,key): self .key = key self .child = [] # Function to convert a tree to its mirror def mirrorTree(root): # Base Case : nothing to do if root is None if root is None : return # Number of children of root n = len (root.child) # If number of child is less than 2 i.e. # 0 or 1 we don't need to do anything if n < 2 : return # Calling mirror function for each child for i in range (n): mirrorTree(root.child[i]); # Reverse variable sized array of child pointers root.child.reverse() # Prints the n-ary tree level wise def printNodeLevelWise(root): if root is None : return # create a queue and enqueue root to it queue = [] queue.append(root) # Do level order traversal. Two loops are used # to make sure that different levels are printed # in different lines while ( len (queue) > 0 ): n = len (queue) while (n > 0 ) : # Dequeue an item from queue and print it p = queue[ 0 ] queue.pop( 0 ) print (p.key,end = " " ) # Enqueue all children of the dequeued item for index, value in enumerate (p.child): queue.append(value) n - = 1 print () # Separator between levels # Driver Program """ Let us create below tree * 10 * / / * 2 34 56 100 * | / | * 1 7 8 9 """ root = Node( 10 ) root.child.append(Node( 2 )) root.child.append(Node( 34 )) root.child.append(Node( 56 )) root.child.append(Node( 100 )) root.child[ 2 ].child.append(Node( 1 )) root.child[ 3 ].child.append(Node( 7 )) root.child[ 3 ].child.append(Node( 8 )) root.child[ 3 ].child.append(Node( 9 )) print ( "Level order traversal Before Mirroring" ) printNodeLevelWise(root) mirrorTree(root) print ( "Level Order traversal After Mirroring" ) printNodeLevelWise(root) |
Javascript
<script> // Javascript program to mirror an n-ary tree // Represents a node of an n-ary tree class Node { constructor() { this .key = 0; this .child = [] } }; // Function to convert a tree to its mirror function mirrorTree(root) { // Base case: Nothing to do if root is null if (root== null ) return ; // Number of children of root var n = root.child.length; // If number of child is less than 2 i.e. // 0 or 1 we do not need to do anything if (n < 2) return ; // Calling mirror function for each child for ( var i=0; i<n; i++) mirrorTree(root.child[i]); // Reverse vector (variable sized array) of child // pointers root.child.reverse(); } // Utility function to create a new tree node function newNode(key) { var temp = new Node; temp.key = key; return temp; } // Prints the n-ary tree level wise function printNodeLevelWise(root) { if (root== null ) return ; // Create a queue and enqueue root to it var q = []; q.push(root); // Do level order traversal. Two loops are used // to make sure that different levels are printed // in different lines while (q.length!=0) { var n = q.length; while (n>0) { // Dequeue an item from queue and print it var p = q[0]; q.shift(); document.write( p.key + " " ); // Enqueue all childrent of the dequeued item for ( var i=0; i<p.child.length; i++) q.push(p.child[i]); n--; } document.write( "<br>" ) // Separator between levels } } // Driver program /* Let us create below tree * 10 * / / * 2 34 56 100 * | / | * 1 7 8 9 */ var root = newNode(10); (root.child).push(newNode(2)); (root.child).push(newNode(34)); (root.child).push(newNode(56)); (root.child).push(newNode(100)); (root.child[2].child).push(newNode(1)); (root.child[3].child).push(newNode(7)); (root.child[3].child).push(newNode(8)); (root.child[3].child).push(newNode(9)); document.write( "Level order traversal Before Mirroring<br>" ); printNodeLevelWise(root); mirrorTree(root); document.write( "<br>Level order traversal After Mirroring<br>" ); printNodeLevelWise(root); // This code is contributed by rrrtnx. </script> |
输出:
Level order traversal Before Mirroring10 2 34 56 100 1 7 8 9 Level order traversal After Mirroring10 100 56 34 2 9 8 7 1
幸亏 尼廷·阿格沃 用于提供初始实施。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写评论
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



