DBMS中冲突可串行性测试的优先图

先决条件： 冲突序列化

优先图 或 序列化图 通常用于测试计划的冲突可序列化性。 它是一个有向图（V，E），由一组节点V={T）组成 _1. T _2. T _3. ……….T _N }和一组有向边E={E _1. E _2. E _3. ……e _M }. 该图包含每个事务T的一个节点 _我 .边缘e _我 是T型的 _j –>T _K T在哪里 _J 是e的起始节点 _我 和T _K 是e的结束节点 _我 .边缘e _我 在节点T之间构造 _J 去 _K 如果T中的一个操作 _J 在T中的某个冲突操作之前出现在计划中 _K .

该算法可以写成：

1. 在图表中为计划中的每个参与事务创建一个节点T。
2. 对于冲突操作，读取和写入项目（X）–如果事务T _J 在T之后执行一个read_项（X） _我 执行写入项（X），从T中绘制边 _我 去 _J 在图表中。
3. 对于冲突的操作，写入项目（X）和读取项目（X）–如果事务T _J 在T之后执行写入_项（X） _我 执行读取项（X），从T中绘制边 _我 去 _J 在图表中。
4. 对于冲突的操作，写入_项（X）和写入_项（X）–如果事务T _J 在T之后执行写入_项（X） _我 执行写入项（X），从T中绘制边 _我 去 _J 在图表中。
5. 如果优先级图中没有循环，则计划S是可序列化的 .

如果优先图中没有循环，这意味着我们可以构造一个与调度S冲突等价的序列调度S。 序列计划可通过以下方式找到： 拓扑排序 非循环优先图的。此类计划可以超过1个。

例如 考虑日程安排：

 S : r1(x) r1(y) w2(x) w1(x) r2(y) 

创建优先级图：

1. 使两个节点对应于事务T _1. T和 _2. .
2. 对于冲突对r1（x）w2（x），其中r1（x）发生在w2（x）之前，从T绘制一条边 _1. 去 _2. .
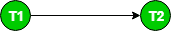
3. 对于冲突对w2（x）w1（x），其中w2（x）发生在w1（x）之前，从T绘制一条边 _2. 去 _1. .

   

因为这个图是循环的，所以我们可以得出这样的结论 不可序列化 任何一个时间表都可以。 让我们尝试使用拓扑排序从该图推断一个序列计划。 边缘 _1. –>T _2. 告诉我 ₁ 应该在T之前 _2. 在线性排序中。 边缘 _2. –>T _1. 告诉我 _2. 应该在T之前 _1. 在线性排序中。 因此，我们无法预测任何特定的顺序（当图形是循环的）。因此，无法从该图中获得序列计划。 考虑另一个时间表S1：

 S1: r1(x) r3(y) w1(x) w2(y) r3(x) w2(x)

该时间表的图表如下：

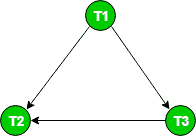
由于该图是非循环的，因此该调度是可冲突序列化的。在这个图上执行拓扑排序会给我们提供一个可能的串行计划，该计划与计划S1冲突。 在拓扑排序中，我们首先选择度为0的节点，即T1。接下来是T3和T2。 所以 S1是冲突可序列化的 既然是 冲突等价物 到 序列表T1 T3 T2。

资料来源：操作系统书、西尔伯沙茨、加尔文和加涅

本文由 萨洛尼巴哈酒店 .如果你喜欢GeekSforgek，并想贡献自己的力量，你也可以使用 写极客。组织 或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上，并帮助其他极客。