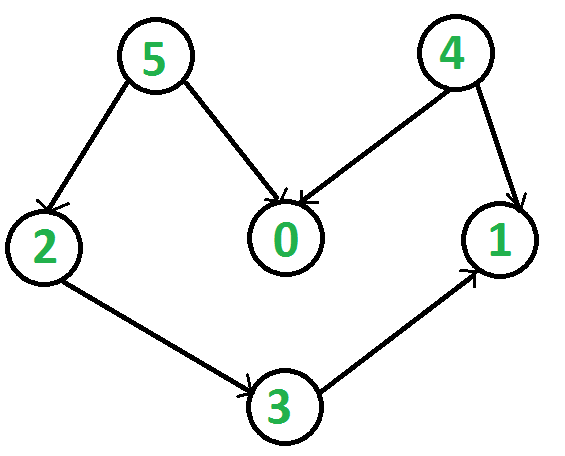
网络拓扑排序 D 定向的 A. 循环的 G raph(DAG)是顶点的线性排序,因此对于每个有向边uv,顶点u在排序中位于v之前。如果图形不是DAG,则无法对其进行拓扑排序。 例如,下列图形的拓扑排序为“5 4 2 3 1 0”。一个图形可以有多个拓扑排序。例如,下列图形的另一个拓扑排序为“4 5 2 0 3 1”。拓扑排序中的第一个顶点始终是阶数为0的顶点(没有后进边的顶点)。
让我们看几个例子,并给出适当的解释, 例子:
输入:
![图片[2]-Kahn拓扑排序算法-yiteyi-C++库](https://www.yiteyi.com/wp-content/uploads/geeks/20200529/geeks_Untitled-Diagram-337.png)
输出: 5 4 2 3 1 0 说明: DAG的拓扑排序是按照这样的顺序进行的,即对于每个有向边uv,顶点u在排序中位于v之前。5没有传入边缘。4没有传入边,2和0有来自4和5的传入边,最后放置1。 输入:
![图片[3]-Kahn拓扑排序算法-yiteyi-C++库](https://www.yiteyi.com/wp-content/uploads/geeks/20200529/geeks_Untitled-Diagram-256.png)
输出: 0 3 4 1 2 说明: 0和3没有传入边,4和1有来自0和3的传入边。2号终于就位了。
A. 基于DFS的拓扑排序解决方案 已经讨论过了。 解决方案 : 在本文中,我们将看到另一种方法来寻找有向无环图(DAG)中顶点的线性排序。该方法基于以下事实: DAG G至少有一个顶点的阶数为0,一个顶点的阶数为0 . 证据: 以上事实有一个简单的证明,一个DAG不包含一个循环,这意味着所有路径都是有限长的。现在让我们来计算从u(源)到v(目标)的最长路径。因为S是最长的路径,所以不可能有到u的输入边和从v的输出边,如果出现这种情况,那么S就不会是最长的路径 =>indegree(u)=0,outdegree(v)=0 算法: 查找DAG拓扑顺序所涉及的步骤: 第一步: 计算DAG中存在的每个顶点的度数(传入边数),并将访问的节点数初始化为0。 第二步: 拾取度为0的所有顶点,并将它们添加到队列中(排队操作) 第三步: 从队列中删除顶点(出列操作),然后单击。
- 将访问的节点数增加1。
- 其所有相邻节点的度数减少1。
- 如果相邻节点的次数减少到零,则将其添加到队列中。
第4步: 重复步骤3,直到队列为空。 第5步: 如果访问的节点数为 不 等于图中的节点数,则给定的图不可能进行拓扑排序。 如何找到每个节点的度? 有两种方法可以计算每个顶点的度数:
- 以度数组为例,它将跟踪 遍历边数组,只需将目标节点的计数器增加1。
for each node in Nodes indegree[node] = 0;for each edge(src, dest) in Edges indegree[dest]++
- 时间复杂度:O(V+E)
- 遍历每个节点的列表,然后将连接到该列表的所有节点的in阶数增加1。
for each node in Nodes If (list[node].size()!=0) then for each dest in list indegree[dest]++;
- 时间复杂度:外部for循环执行V次,内部for循环执行E次,因此总体时间复杂度为O(V+E)。 该算法的总体时间复杂度为O(V+E)
下面是C++实现上述算法。该实现使用上面讨论的方法2来查找度。
C++
// A C++ program to print topological // sorting of a graph using indegrees. #include <bits/stdc++.h> using namespace std; // Class to represent a graph class Graph { // No. of vertices' int V; // Pointer to an array containing // adjacency listsList list< int >* adj; public : // Constructor Graph( int V); // Function to add an edge to graph void addEdge( int u, int v); // prints a Topological Sort of // the complete graph void topologicalSort(); }; Graph::Graph( int V) { this ->V = V; adj = new list< int >[V]; } void Graph::addEdge( int u, int v) { adj[u].push_back(v); } // The function to do // Topological Sort. void Graph::topologicalSort() { // Create a vector to store // indegrees of all // vertices. Initialize all // indegrees as 0. vector< int > in_degree(V, 0); // Traverse adjacency lists // to fill indegrees of // vertices. This step // takes O(V+E) time for ( int u = 0; u < V; u++) { list< int >::iterator itr; for (itr = adj[u].begin(); itr != adj[u].end(); itr++) in_degree[*itr]++; } // Create an queue and enqueue // all vertices with indegree 0 queue< int > q; for ( int i = 0; i < V; i++) if (in_degree[i] == 0) q.push(i); // Initialize count of visited vertices int cnt = 0; // Create a vector to store // result (A topological // ordering of the vertices) vector< int > top_order; // One by one dequeue vertices // from queue and enqueue // adjacents if indegree of // adjacent becomes 0 while (!q.empty()) { // Extract front of queue // (or perform dequeue) // and add it to topological order int u = q.front(); q.pop(); top_order.push_back(u); // Iterate through all its // neighbouring nodes // of dequeued node u and // decrease their in-degree // by 1 list< int >::iterator itr; for (itr = adj[u].begin(); itr != adj[u].end(); itr++) // If in-degree becomes zero, // add it to queue if (--in_degree[*itr] == 0) q.push(*itr); cnt++; } // Check if there was a cycle if (cnt != V) { cout << "There exists a cycle in the graph" ; return ; } // Print topological order for ( int i = 0; i < top_order.size(); i++) cout << top_order[i] << " " ; cout << endl; } // Driver program to test above functions int main() { // Create a graph given in the // above diagram Graph g(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); cout << "Following is a Topological Sort of" ; g.topologicalSort(); return 0; } |
JAVA
// A Java program to print topological // sorting of a graph using indegrees import java.util.*; // Class to represent a graph class Graph { // No. of vertices int V; // An Array of List which contains // references to the Adjacency List of // each vertex List<Integer> adj[]; // Constructor public Graph( int V) { this .V = V; adj = new ArrayList[V]; for ( int i = 0 ; i < V; i++) adj[i] = new ArrayList<Integer>(); } // Function to add an edge to graph public void addEdge( int u, int v) { adj[u].add(v); } // prints a Topological Sort of the // complete graph public void topologicalSort() { // Create a array to store // indegrees of all // vertices. Initialize all // indegrees as 0. int indegree[] = new int [V]; // Traverse adjacency lists // to fill indegrees of // vertices. This step takes // O(V+E) time for ( int i = 0 ; i < V; i++) { ArrayList<Integer> temp = (ArrayList<Integer>)adj[i]; for ( int node : temp) { indegree[node]++; } } // Create a queue and enqueue // all vertices with indegree 0 Queue<Integer> q = new LinkedList<Integer>(); for ( int i = 0 ; i < V; i++) { if (indegree[i] == 0 ) q.add(i); } // Initialize count of visited vertices int cnt = 0 ; // Create a vector to store result // (A topological ordering of the vertices) Vector<Integer> topOrder = new Vector<Integer>(); while (!q.isEmpty()) { // Extract front of queue // (or perform dequeue) // and add it to topological order int u = q.poll(); topOrder.add(u); // Iterate through all its // neighbouring nodes // of dequeued node u and // decrease their in-degree // by 1 for ( int node : adj[u]) { // If in-degree becomes zero, // add it to queue if (--indegree[node] == 0 ) q.add(node); } cnt++; } // Check if there was a cycle if (cnt != V) { System.out.println( "There exists a cycle in the graph" ); return ; } // Print topological order for ( int i : topOrder) { System.out.print(i + " " ); } } } // Driver program to test above functions class Main { public static void main(String args[]) { // Create a graph given in the above diagram Graph g = new Graph( 6 ); g.addEdge( 5 , 2 ); g.addEdge( 5 , 0 ); g.addEdge( 4 , 0 ); g.addEdge( 4 , 1 ); g.addEdge( 2 , 3 ); g.addEdge( 3 , 1 ); System.out.println( "Following is a Topological Sort" ); g.topologicalSort(); } } |
Python3
# A Python program to print topological sorting of a graph # using indegrees from collections import defaultdict # Class to represent a graph class Graph: def __init__( self , vertices): self .graph = defaultdict( list ) # dictionary containing adjacency List self .V = vertices # No. of vertices # function to add an edge to graph def addEdge( self , u, v): self .graph[u].append(v) # The function to do Topological Sort. def topologicalSort( self ): # Create a vector to store indegrees of all # vertices. Initialize all indegrees as 0. in_degree = [ 0 ] * ( self .V) # Traverse adjacency lists to fill indegrees of # vertices. This step takes O(V + E) time for i in self .graph: for j in self .graph[i]: in_degree[j] + = 1 # Create an queue and enqueue all vertices with # indegree 0 queue = [] for i in range ( self .V): if in_degree[i] = = 0 : queue.append(i) # Initialize count of visited vertices cnt = 0 # Create a vector to store result (A topological # ordering of the vertices) top_order = [] # One by one dequeue vertices from queue and enqueue # adjacents if indegree of adjacent becomes 0 while queue: # Extract front of queue (or perform dequeue) # and add it to topological order u = queue.pop( 0 ) top_order.append(u) # Iterate through all neighbouring nodes # of dequeued node u and decrease their in-degree # by 1 for i in self .graph[u]: in_degree[i] - = 1 # If in-degree becomes zero, add it to queue if in_degree[i] = = 0 : queue.append(i) cnt + = 1 # Check if there was a cycle if cnt ! = self .V: print ( "There exists a cycle in the graph" ) else : # Print topological order print (top_order) g = Graph( 6 ) g.addEdge( 5 , 2 ); g.addEdge( 5 , 0 ); g.addEdge( 4 , 0 ); g.addEdge( 4 , 1 ); g.addEdge( 2 , 3 ); g.addEdge( 3 , 1 ); print ( "Following is a Topological Sort of the given graph" ) g.topologicalSort() # This code is contributed by Neelam Yadav |
Javascript
<script> // A Javascript program to print topological // sorting of a graph using indegrees // No. of vertices let V; // An Array of List which contains // references to the Adjacency List of // each vertex let adj; function Graph(v) { V = v; adj = new Array(V); for (let i = 0; i < V; i++) adj[i] = []; } // Function to add an edge to graph function addEdge(u, v) { adj[u].push(v); } // prints a Topological Sort of the // complete graph function topologicalSort() { // Create a array to store // indegrees of all // vertices. Initialize all // indegrees as 0. let indegree = new Array(V); for (let i = 0; i < V; i++) indegree[i] = 0; // Traverse adjacency lists // to fill indegrees of // vertices. This step takes // O(V+E) time for (let i = 0; i < V; i++) { let temp = adj[i]; for (let node = 0; node < temp.length; node++) { indegree[temp[node]]++; } } // Create a queue and enqueue // all vertices with indegree 0 let q = []; for (let i = 0; i < V; i++) { if (indegree[i] == 0) q.push(i); } // Initialize count of visited vertices let cnt = 0; // Create a vector to store result // (A topological ordering of the vertices) let topOrder = []; while (q.length!=0) { // Extract front of queue // (or perform dequeue) // and add it to topological order let u = q.shift(); topOrder.push(u); // Iterate through all its // neighbouring nodes // of dequeued node u and // decrease their in-degree // by 1 for (let node = 0; node < adj[u].length; node++) { // If in-degree becomes zero, // add it to queue if (--indegree[adj[u][node]] == 0) q.push(adj[u][node]); } cnt++; } // Check if there was a cycle if (cnt != V) { document.write( "There exists a cycle in the graph" ); return ; } // Print topological order for (let i = 0; i < topOrder.length; i++) { document.write(topOrder[i] + " " ); } } // Driver program to test above functions // Create a graph given in the above diagram Graph(6); addEdge(5, 2); addEdge(5, 0); addEdge(4, 0); addEdge(4, 1); addEdge(2, 3); addEdge(3, 1); document.write( "Following is a Topological Sort<br>" ); topologicalSort(); // This code is contributed by avanitrachhadiya2155 </script> |
输出:
Following is a Topological Sort4 5 2 0 3 1
复杂性分析:
- 时间复杂性: O(V+E)。 外部for循环将执行V次,内部for循环将执行E次。
- 辅助空间: O(V)。 队列需要存储图形的所有顶点。所以所需的空间是O(V)
本文由 希拉格·阿加瓦尔 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



