Adobe面试经验|第23组（1年经验）-yiteyi-C++库

我最近在奥多比诺伊达办公室接受了面试，得到了这份工作。我有一年的工作经验。

null

这是一个标准流程，包括对Hackerrank的能力和技术测试。每次都一样。你可以看看以前的档案中的测试。

筛选
- 能力倾向测试
- 技术测试有13个MCQ和7个标准编码问题。
诺伊达办公室的采访
第一轮。
1. 与C、C++相关的问题是什么？h文件加载并链接到它们的。c文件。我对这件事了解不多，因为我有Java方面的经验，并用Java告诉了他同样的答案。
2. 如何在旋转数组中找到最小元素 ? e、 g.4 5 6 1 2 3 用二进制搜索给出了答案
3. 如何在两个链表之间找到公共节点 ?
```
1→2→3→4→NULL
      |
     5→6
```
  使用LLs长度的差异给出了答案，并编写了处理所有案例的代码。
4. 然后，他讨论了操作系统的概念、虚拟内存、分页等。
笔记 .确保你编写的代码能够处理所有的测试用例，尤其是边界测试用例。
第二轮。
1. 之后，他只问了我一个与几何有关的问题。这个问题是一个等腰直角三角形。求较小圆的半径。
用毕达哥拉斯基本定理解决了这个问题。

奇怪的是，他只问了一个问题。
第三轮
这一轮很棘手。
1. 问题是一个长度为l、宽度为b的矩形ABCD。现在它沿着对角线BD折叠。即a与C连接。求线段EF的长度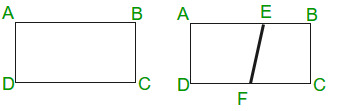用他的暗示解决了这个问题。基本上，它涉及到一些与想象和毕达哥拉斯定理有关的推论。基本上AE=EC和EF=EC。然后是简单的几何问题。
2. 你如何处理一个数组？所涉及的时间复杂性是什么？显然，他对确切的复杂性很感兴趣。我告诉他，我们总是从数组中索引为（n-1）/2的最后一个父级开始计算。
  然后他问我如何对单个元素进行堆化，以及堆排序是如何工作的。
  
  基本上，他想让我回答，我们不把元素从（n-1）/2堆到n，这降低了我最后回答的nlogn的时间复杂度。
3. ```
int a = 8;
char *b = (int *) a;
```
  b指的是哪里？
  
  这个问题和Big endian和little endian有关，因为他想让我问建筑技术是little endian还是Big endian。我告诉他我不知道这件事。
  
  问完这个问题后，我告诉他我有机械方面的背景，对计算机体系结构知之甚少。他有点震惊，跳过了操作系统的问题。我真幸运！！！
4. 如何知道一个数字是O（1）中2的幂？n&（n–1）=0？对：错
5. 给定一个数字数组，所有这些数字都是重复的，只有一个不重复的，找出不重复的数字 .
  给出了使用XOR的算法。
6. 然后他扩展了前一个问题，以发现两个数字是否不重复。他想再次使用XOR方法。
7. 给定两棵二叉树A和B。检查B是否是A的子树 .使用常规树遍历解决。
8. 在未排序的数字数组中找到第k个最小元素。
首先给出了使用堆的方法。将数组的所有元素放入一个最小堆中，并提取k次。但他对更好的方法感兴趣。

使用快速选择算法（修改后的快速排序）回答。

他告诉我，有一种更优化的方法可以使用顺序统计来选择枢轴元素。我不知道顺序统计法，但他对基本的快速选择算法非常满意。
第四轮：导演轮
1. 我的简要介绍。为什么CGPA低，等等？
2. 给定一个大小为m的数组，其中分配了n个索引。在这个数组中搜索一个元素时，如何最大限度地减少比较次数？
  我写了基本的线性搜索代码。然后他问我如何减少比较的次数。
3. 给定平面上形成多边形的n个点。找出该多边形内是否存在随机点？
4. 你如何计算一个湖泊的体积。他对我的方法很感兴趣。我给出了2-3种方法，其中一种很有趣，他嘲笑我。

最后，他问我是否有关于这个角色和其他方面的问题。

我想花点时间感谢Geeksforgeks帮我准备面试。为你们干杯！！！

如果你喜欢Geeksforgek，并想贡献自己的力量，你也可以写一篇文章，然后把你的文章发到contribute@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上，并帮助其他极客。

Adobe的所有练习题 !

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章