斯坦纳树问题

什么是斯坦纳树？ 给出一个图表和一个 子集 对于图中的顶点，steiner树跨越给定的子集。Steiner树可能包含一些不在给定子集中但用于连接子集顶点的顶点。

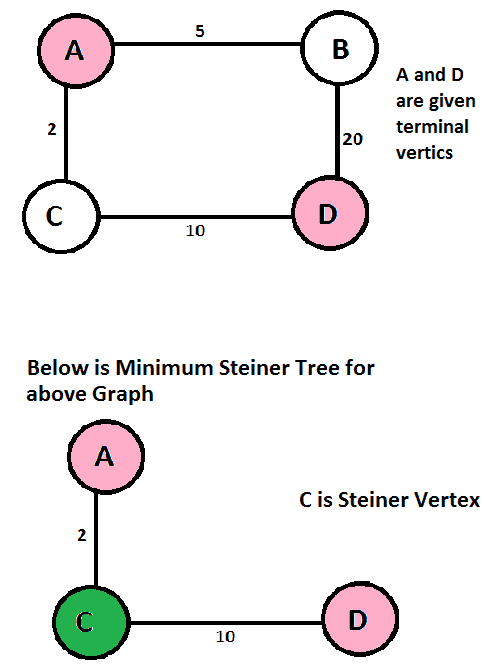
给定的顶点集称为 终端顶点 用于构造Steiner树的其他顶点称为 施泰纳顶点 . 斯坦纳树问题 就是找到最小成本的斯坦纳树。下面是一个例子。

生成树与斯坦纳树 最小生成树i 这是一棵最小重量的树，跨越 全部的 顶点。

如果给定的子集（或终端）顶点等于Steiner树问题中所有顶点的集合，则该问题成为最小生成树问题。如果给定的子集只包含两个顶点，那么它就是两个顶点之间的最短路径问题。

求最小生成树是多项式时间可解的，但最小Steiner树问题是NP难问题，相关的决策问题是NP完全问题。

Steiner树的应用 任何一种情况下，任务是最小化一些重要位置之间的连接成本，如VLSI设计、计算机网络等。

基于最短路径的近似算法 由于Steiner树问题是NP难问题，所以没有多项式时间解总是给出最优代价。因此，有近似算法来解决同样的问题。下面是一个简单的近似算法。

1) Start with a subtree T consisting of 
   one given terminal vertex
2) While T does not span all terminals
   a) Select a terminal x not in T that is closest 
      to a vertex in T.
   b) Add to T the shortest path that connects x with T

上述算法是（2-2/n）近似的，即它保证了对于给定的有n个顶点的图，该算法产生的解不超过优化解的这个比例。还有更好的算法可以提供更好的比率。有关更多详细信息，请参阅下面的参考资料。

参考资料： www.cs。uu。nl/docs/vakken/an/teoud/an steiner。幻灯片演示文件

本文由 希瓦姆·古普塔 。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请发表评论