欧几里德算法（基本和扩展）-yiteyi-C++库

两个数的GCD是将两个数相除的最大数。求GCD的一个简单方法是将两个数分解并乘以公共素数因子。

null

GCD

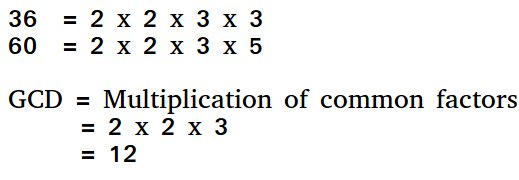
GCD的基本欧几里德算法 该算法基于以下事实。

如果我们从一个较大的数字中减去一个较小的数字（我们减少了一个较大的数字），GCD不会改变。因此，如果我们不断重复减去两个中较大的一个，我们最终得到的是GCD。
现在不是减法，如果我们除以较小的数字，当我们找到余数0时，算法停止。

下面是使用欧几里德算法计算gcd的递归函数。

CPP

                         // C++ program to demonstrate                       
                         // Basic Euclidean Algorithm                       
                         #include <bits/stdc++.h>                       
                         using                                     namespace                                     std;                       
           
                         // Function to return                       
                         // gcd of a and b                       
                         int                                     gcd(                                     int                                     a,                                     int                                     b)                       
                         {                       
                                                 if                                     (a == 0)                       
                                                 return                                     b;                       
                                                 return                                     gcd(b % a, a);                       
                         }                       
           
                         // Driver Code                       
                         int                                     main()                       
                         {                       
                                                 int                                     a = 10, b = 15;                       
                                                 cout <<                                     "GCD("                                     << a <<                                     ", "                       
                                                 << b <<                                     ") = "                                     << gcd(a, b)                       
                                                 << endl;                       
                                                 a = 35, b = 10;                       
                                                 cout <<                                     "GCD("                                     << a <<                                     ", "                       
                                                 << b <<                                     ") = "                                     << gcd(a, b)                       
                                                 << endl;                       
                                                 a = 31, b = 2;                       
                                                 cout <<                                     "GCD("                                     << a <<                                     ", "                       
                                                 << b <<                                     ") = "                                     << gcd(a, b)                       
                                                 << endl;                       
                                                 return                                     0;                       
                         }                       
           
                         // This code is contributed                       
                         // by Nimit Garg                       

C

                         // C program to demonstrate Basic Euclidean Algorithm                       
                         #include <stdio.h>                       
           
                         // Function to return gcd of a and b                       
                         int                                     gcd(                                     int                                     a,                                     int                                     b)                       
                         {                       
                                                 if                                     (a == 0)                       
                                                 return                                     b;                       
                                                 return                                     gcd(b%a, a);                       
                         }                       
           
                         // Driver program to test above function                       
                         int                                     main()                       
                         {                       
                                                 int                                     a = 10, b = 15;                       
                                                 printf                                     (                                     "GCD(%d, %d) = %dn"                                     , a, b, gcd(a, b));                       
                                                 a = 35, b = 10;                       
                                                 printf                                     (                                     "GCD(%d, %d) = %dn"                                     , a, b, gcd(a, b));                       
                                                 a = 31, b = 2;                       
                                                 printf                                     (                                     "GCD(%d, %d) = %dn"                                     , a, b, gcd(a, b));                       
                                                 return                                     0;                       
                         }                       

JAVA

                         // Java program to demonstrate working of extended                       
                         // Euclidean Algorithm                       
           
                         import                                     java.util.*;                       
                         import                                     java.lang.*;                       
           
                         class                                     GFG                       
                         {                       
                                                 // extended Euclidean Algorithm                       
                                                 public                                     static                                     int                                     gcd(                                     int                                     a,                                     int                                     b)                       
                                                 {                       
                                                 if                                     (a ==                                     0                                     )                       
                                                 return                                     b;                       
                                   
                                                 return                                     gcd(b%a, a);                       
                                                 }                       
           
                         // Driver Program                       
                                                 public                                     static                                     void                                     main(String[] args)                       
                                                 {                       
                                                 int                                     a =                                     10                                     , b =                                     15                                     , g;                       
                                                 g = gcd(a, b);                       
                                                 System.out.println(                                     "GCD("                                     + a +                                     " , "                                     + b+                                     ") = "                                     + g);                       
                                   
                                                 a =                                     35                                     ; b =                                     10                                     ;                       
                                                 g = gcd(a, b);                       
                                                 System.out.println(                                     "GCD("                                     + a +                                     " , "                                     + b+                                     ") = "                                     + g);                       
                                   
                                                 a =                                     31                                     ; b =                                     2                                     ;                       
                                                 g = gcd(a, b);                       
                                                 System.out.println(                                     "GCD("                                     + a +                                     " , "                                     + b+                                     ") = "                                     + g);                       
           
                                                 }                       
                         }                       
                         // Code Contributed by Mohit Gupta_OMG <(0_o)>                       

Python3

                         # Python program to demonstrate Basic Euclidean Algorithm                       
           
           
                         # Function to return gcd of a and b                       
                         def                                     gcd(a, b):                       
                                                 if                                     a                                     =                                     =                                     0                                     :                       
                                                 return                                     b                       
                                   
                                                 return                                     gcd(b                                     %                                     a, a)                       
           
                         a                                     =                                     10                       
                         b                                     =                                     15                       
                         print                                     (                                     "gcd("                                     , a ,                                     ","                                     , b,                                     ") = "                                     , gcd(a, b))                       
           
                         a                                     =                                     35                       
                         b                                     =                                     10                       
                         print                                     (                                     "gcd("                                     , a ,                                     ","                                     , b,                                     ") = "                                     , gcd(a, b))                       
           
                         a                                     =                                     31                       
                         b                                     =                                     2                       
                         print                                     (                                     "gcd("                                     , a ,                                     ","                                     , b,                                     ") = "                                     , gcd(a, b))                       
           
                         # Code Contributed By Mohit Gupta_OMG <(0_o)>                       

C#

                         using                                     System;                       
           
                         class                                     GFG                       
                         {                       
                                                 public                                     static                                     int                                     gcd(                                     int                                     a,                                     int                                     b)                       
                                                 {                       
                                                 if                                     (a == 0)                       
                                                 return                                     b;                       
                                   
                                                 return                                     gcd(b % a, a);                       
                                                 }                       
                                   
                                                 // Driver Code                       
                                                 static                                     public                                     void                                     Main ()                       
                                                 {                       
                                                 int                                     a = 10, b = 15, g;                       
                                                 g = gcd(a, b);                       
                                                 Console.WriteLine(                                     "GCD("                                     + a +                       
                                                 " , "                                     + b +                                     ") = "                                     + g);                       
                                   
                                                 a = 35; b = 10;                       
                                                 g = gcd(a, b);                       
                                                 Console.WriteLine(                                     "GCD("                                     + a +                       
                                                 " , "                                     + b +                                     ") = "                                     + g);                       
                                   
                                                 a = 31; b = 2;                       
                                                 g = gcd(a, b);                       
                                                 Console.WriteLine(                                     "GCD("                                     + a +                       
                                                 " , "                                     + b +                                     ") = "                                     + g);                       
                                                 }                       
                         }                       
           
                         // This code is contributed by ajit                       

PHP

                         <?php                       
                         // PHP program to demonstrate                       
                         // Basic Euclidean Algorithm                       
           
                         // Function to return                       
                         // gcd of a and b                       
                         function                                     gcd(                                     $a                                     ,                                     $b                                     )                       
                         {                       
                                                 if                                     (                                     $a                                     == 0)                       
                                                 return                                     $b                                     ;                       
                                                 return                                     gcd(                                     $b                                     %                                     $a                                     ,                                     $a                                     );                       
                         }                       
           
                         // Driver Code                       
                         $a                                     = 10;                                     $b                                     = 15;                       
                         echo                                     "GCD("                                     ,                                     $a                                     ,                                     ","                                     ,                                     $b                                     ,                                     ") = "                                     ,                       
                                                 gcd(                                     $a                                     ,                                     $b                                     );                       
                         echo                                     ""                                     ;                       
                         $a                                     = 35;                                     $b                                     = 10;                       
                         echo                                     "GCD("                                     ,                                     $a                                     ,                                     ","                                     ,                                     $b                                     ,                                     ") = "                                     ,                       
                                                 gcd(                                     $a                                     ,                                     $b                                     );                       
                         echo                                     ""                                     ;                       
                         $a                                     = 31;                                     $b                                     = 2;                       
                         echo                                     "GCD("                                     ,                                     $a                                     ,                                     ","                                     ,                                     $b                                     ,                                     ") = "                                     ,                       
                                                 gcd(                                     $a                                     ,                                     $b                                     );                       
           
                         // This code is contributed by m_kit                       
                         ?>                       

Javascript

                         <script>                       
           
                         // JavaScript program to demonstrate                       
                         // Basic Euclidean Algorithm                       
           
                         // Function to return                       
                         // gcd of a and b                       
                         function                                     gcd( a,  b)                       
                         {                       
                                                 if                                     (a == 0)                       
                                                 return                                     b;                       
                                                 return                                     gcd(b % a, a);                       
                         }                       
           
                         // Driver Code                       
           
                                                 let a = 10, b = 15;                       
                                                 document.write(                                     "GCD("                                     + a +                                     ", "                       
                                                 + b +                                     ") = "                                     + gcd(a, b) +                                     "<br/>"                                     );                       
                                   
                                                 a = 35, b = 10;                       
                                                 document.write(                                     "GCD("                                     + a +                                     ", "                       
                                                 + b +                                     ") = "                                     + gcd(a, b) +                                     "<br/>"                                     );                       
                                   
                                                 a = 31, b = 2;                       
                                                 document.write(                                     "GCD("                                     + a +                                     ", "                       
                                                 + b +                                     ") = "                                     + gcd(a, b) +                                     "<br/>"                                     );                       
           
                         // This code contributed by aashish1995                       
           
                         </script>                       

输出：

GCD(10, 15) = 5GCD(35, 10) = 5GCD(31, 2) = 1

时间复杂性： O（对数最大值（a，b）） 扩展欧几里德算法： 扩展的欧几里德算法还可以找到整数系数x和y，以便：

  ax + by = gcd(a, b)

例如：

Input: a = 30, b = 20Output: gcd = 10        x = 1, y = -1(Note that 30*1 + 20*(-1) = 10)Input: a = 35, b = 15Output: gcd = 5        x = 1, y = -2(Note that 35*1 + 15*(-2) = 5)

扩展的欧几里德算法使用递归调用gcd（b%a，a）计算的结果更新gcd（a，b）的结果。让递归调用计算的x和y的值为x _1. 还有y _1. .x和y使用以下表达式进行更新。

x = y₁ - ⌊b/a⌋ * x₁y = x₁

建议：请在“上解决” 实践 “首先，在讨论解决方案之前。

下面是基于上述公式的实现。

C++

                         // C++ program to demonstrate working of                       
                         // extended Euclidean Algorithm                       
                         #include <bits/stdc++.h>                       
                         using                                     namespace                                     std;                       
           
                         // Function for extended Euclidean Algorithm                       
                         int                                     gcdExtended(                                     int                                     a,                                     int                                     b,                                     int                                     *x,                                     int                                     *y)                       
                         {                       
                                                 // Base Case                       
                                                 if                                     (a == 0)                       
                                                 {                       
                                                 *x = 0;                       
                                                 *y = 1;                       
                                                 return                                     b;                       
                                                 }                       
           
                                                 int                                     x1, y1;                                     // To store results of recursive call                       
                                                 int                                     gcd = gcdExtended(b%a, a, &x1, &y1);                       
           
                                                 // Update x and y using results of                       
                                                 // recursive call                       
                                                 *x = y1 - (b/a) * x1;                       
                                                 *y = x1;                       
           
                                                 return                                     gcd;                       
                         }                       
           
                         // Driver Code                       
                         int                                     main()                       
                         {                       
                                                 int                                     x, y, a = 35, b = 15;                       
                                                 int                                     g = gcdExtended(a, b, &x, &y);                       
                                                 cout <<                                     "GCD("                                     << a <<                                     ", "                                     << b                       
                                                 <<                                     ") = "                                     << g << endl;                       
                                                 return                                     0;                       
                         }                       
           
                         // This code is contributed by TusharSabhani                       

C

                         // C program to demonstrate working of extended                       
                         // Euclidean Algorithm                       
                         #include <stdio.h>                       
           
                         // C function for extended Euclidean Algorithm                       
                         int                                     gcdExtended(                                     int                                     a,                                     int                                     b,                                     int                                     *x,                                     int                                     *y)                       
                         {                       
                                                 // Base Case                       
                                                 if                                     (a == 0)                       
                                                 {                       
                                                 *x = 0;                       
                                                 *y = 1;                       
                                                 return                                     b;                       
                                                 }                       
           
                                                 int                                     x1, y1;                                     // To store results of recursive call                       
                                                 int                                     gcd = gcdExtended(b%a, a, &x1, &y1);                       
           
                                                 // Update x and y using results of recursive                       
                                                 // call                       
                                                 *x = y1 - (b/a) * x1;                       
                                                 *y = x1;                       
           
                                                 return                                     gcd;                       
                         }                       
           
                         // Driver Program                       
                         int                                     main()                       
                         {                       
                                                 int                                     x, y;                       
                                                 int                                     a = 35, b = 15;                       
                                                 int                                     g = gcdExtended(a, b, &x, &y);                       
                                                 printf                                     (                                     "gcd(%d, %d) = %d"                                     , a, b, g);                       
                                                 return                                     0;                       
                         }                       

JAVA

                         // Java program to demonstrate working of extended                       
                         // Euclidean Algorithm                       
           
                         import                                     java.util.*;                       
                         import                                     java.lang.*;                       
           
                         class                                     GFG                       
                         {                       
                                                 // extended Euclidean Algorithm                       
                                                 public                                     static                                     int                                     gcdExtended(                                     int                                     a,                                     int                                     b,                                     int                                     x,                                     int                                     y)                       
                                                 {                       
                                                 // Base Case                       
                                                 if                                     (a ==                                     0                                     )                       
                                                 {                       
                                                 x =                                     0                                     ;                       
                                                 y =                                     1                                     ;                       
                                                 return                                     b;                       
                                                 }                       
           
                                                 int                                     x1=                                     1                                     , y1=                                     1                                     ;                                     // To store results of recursive call                       
                                                 int                                     gcd = gcdExtended(b%a, a, x1, y1);                       
           
                                                 // Update x and y using results of recursive                       
                                                 // call                       
                                                 x = y1 - (b/a) * x1;                       
                                                 y = x1;                       
           
                                                 return                                     gcd;                       
                                                 }                       
           
                         // Driver Program                       
                                                 public                                     static                                     void                                     main(String[] args)                       
                                                 {                       
                                                 int                                     x=                                     1                                     , y=                                     1                                     ;                       
                                                 int                                     a =                                     35                                     , b =                                     15                                     ;                       
                                                 int                                     g = gcdExtended(a, b, x, y);                       
                                                 System.out.print(                                     "gcd("                                     + a +                                     " , "                                     + b+                                     ") = "                                     + g);                       
           
                                                 }                       
                         }                       
                         // Code Contributed by Mohit Gupta_OMG <(0-o)>                       

Python3

                         # Python program to demonstrate working of extended                       
                         # Euclidean Algorithm                       
                                   
                         # function for extended Euclidean Algorithm                       
                         def                                     gcdExtended(a, b):                       
           
                                                 # Base Case                       
                                                 if                                     a                                     =                                     =                                     0                                     :                       
                                                 return                                     b,                                     0                                     ,                                     1                       
                                   
                                                 gcd, x1, y1                                     =                                     gcdExtended(b                                     %                                     a, a)                       
                                   
                                                 # Update x and y using results of recursive                       
                                                 # call                       
                                                 x                                     =                                     y1                                     -                                     (b                                     /                                     /                                     a)                                     *                                     x1                       
                                                 y                                     =                                     x1                       
                                   
                                                 return                                     gcd, x, y                       
                                   
           
                         # Driver code                       
                         a, b                                     =                                     35                                     ,                                     15                       
                         g, x, y                                     =                                     gcdExtended(a, b)                       
                         print                                     (                                     "gcd("                                     , a ,                                     ","                                     , b,                                     ") = "                                     , g)                       

C#

                         // C# program to demonstrate working                       
                         // of extended Euclidean Algorithm                       
                         using                                     System;                       
           
                         class                                     GFG                       
                         {                       
                                   
                                                 // extended Euclidean Algorithm                       
                                                 public                                     static                                     int                                     gcdExtended(                                     int                                     a,                                     int                                     b,                       
                                                 int                                     x,                                     int                                     y)                       
                                                 {                       
                                                 // Base Case                       
                                                 if                                     (a == 0)                       
                                                 {                       
                                                 x = 0;                       
                                                 y = 1;                       
                                                 return                                     b;                       
                                                 }                       
           
                                                 // To store results of                       
                                                 // recursive call                       
                                                 int                                     x1 = 1, y1 = 1;                       
                                                 int                                     gcd = gcdExtended(b % a, a, x1, y1);                       
           
                                                 // Update x and y using                       
                                                 // results of recursive call                       
                                                 x = y1 - (b / a) * x1;                       
                                                 y = x1;                       
           
                                                 return                                     gcd;                       
                                                 }                       
                                   
                                                 // Driver Code                       
                                                 static                                     public                                     void                                     Main ()                       
                                                 {                       
                                                 int                                     x = 1, y = 1;                       
                                                 int                                     a = 35, b = 15;                       
                                                 int                                     g = gcdExtended(a, b, x, y);                       
                                                 Console.WriteLine(                                     "gcd("                                     + a +                                     " , "                                     +                       
                                                 b +                                     ") = "                                     + g);                       
                                                 }                       
                         }                       
           
                         // This code is contributed by m_kit                       

PHP

                         <?php                       
                         // PHP program to demonstrate                       
                         // working of extended                       
                         // Euclidean Algorithm                       
           
                         // PHP function for                       
                         // extended Euclidean                       
                         // Algorithm                       
                         function                                     gcdExtended(                                     $a                                     ,                                     $b                                     ,                       
                                                 $x                                     ,                                     $y                                     )                       
                         {                       
                                                 // Base Case                       
                                                 if                                     (                                     $a                                     == 0)                       
                                                 {                       
                                                 $x                                     = 0;                       
                                                 $y                                     = 1;                       
                                                 return                                     $b                                     ;                       
                                                 }                       
           
                                                 // To store results                       
                                                 // of recursive call                       
                                                 $gcd                                     = gcdExtended(                                     $b                                     %                                     $a                                     ,                       
                                                 $a                                     ,                                     $x                                     ,                                     $y                                     );                       
           
                                                 // Update x and y using                       
                                                 // results of recursive                       
                                                 // call                       
                                                 $x                                     =                                     $y                                     -                                     floor                                     (                                     $b                                     /                                     $a                                     ) *                                     $x                                     ;                       
                                                 $y                                     =                                     $x                                     ;                       
           
                                                 return                                     $gcd                                     ;                       
                         }                       
           
                         // Driver Code                       
                         $x                                     = 0;                       
                         $y                                     = 0;                       
                         $a                                     = 35;                                     $b                                     = 15;                       
                         $g                                     = gcdExtended(                                     $a                                     ,                                     $b                                     ,                                     $x                                     ,                                     $y                                     );                       
                         echo                                     "gcd("                                     ,                                     $a                                     ;                       
                         echo                                     ", "                                     ,                                     $b                                     ,                                     ")"                                     ;                       
                         echo                                     " = "                                     ,                                     $g                                     ;                       
           
                         // This code is contributed by ajit                       
                         ?>                       

Javascript

                         <script>                       
           
                         // Javascript program to demonstrate                       
                         // working of extended                       
                         // Euclidean Algorithm                       
           
                         // Javascript function for                       
                         // extended Euclidean                       
                         // Algorithm                       
                         function                                     gcdExtended(a, b,                       
                                                 x, y)                       
                         {                       
                                                 // Base Case                       
                                                 if                                     (a == 0)                       
                                                 {                       
                                                 x = 0;                       
                                                 y = 1;                       
                                                 return                                     b;                       
                                                 }                       
           
                                                 // To store results                       
                                                 // of recursive call                       
                                                 let gcd = gcdExtended(b % a,                       
                                                 a, x, y);                       
           
                                                 // Update x and y using                       
                                                 // results of recursive                       
                                                 // call                       
                                                 x = y - (b / a) * x;                       
                                                 y = x;                       
           
                                                 return                                     gcd;                       
                         }                       
           
                         // Driver Code                       
                         let x = 0;                       
                         let y = 0;                       
                         let a = 35;                       
                         let b = 15;                       
                         let g = gcdExtended(a, b, x, y);                       
                         document.write(                                     "gcd("                                     + a);                       
                         document.write(                                     ", "                                     + b +                                     ")"                                     );                       
                         document.write(                                     " = "                                     + g);                       
           
                         // This code is contributed by _saurabh_jaiswal                       
           
                         </script>                       

输出：

gcd(35, 15) = 5

扩展算法是如何工作的？

As seen above, x and y are results for inputs a and b,   a.x + b.y = gcd                      ----(1)  And x₁ and y₁ are results for inputs b%a and a   (b%a).x₁ + a.y₁ = gcd                       When we put b%a = (b - (⌊b/a⌋).a) in above, we get following. Note that ⌊b/a⌋ is floor(b/a)   (b - (⌊b/a⌋).a).x₁ + a.y₁  = gcdAbove equation can also be written as below   b.x₁ + a.(y₁ - (⌊b/a⌋).x₁) = gcd      ---(2)After comparing coefficients of 'a' and 'b' in (1) and (2), we get following   x = y₁ - ⌊b/a⌋ * x₁   y = x₁

扩展算法如何有用？ 当a和b是互质（或gcd为1）时，扩展的欧几里德算法特别有用。因为x是“a模b”的模乘逆，y是“b模a”的模乘逆。特别是模乘逆的计算是RSA公钥加密方法中的一个重要步骤。 参考资料： http://e-maxx.ru/algo/extended_euclid_algorithm http://en.wikipedia.org/wiki/Euclidean_algorithm http://en.wikipedia.org/wiki/Extended_Euclidean_algorithm 本文由 安克尔 。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请发表评论

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章