给定n个城市和每对城市之间的距离,选择k个城市放置仓库(或ATM或云服务器),以使城市到仓库(或ATM或云服务器)的最大距离最小化。
例如,考虑以下四个城市,0, 1, 2个和3个,以及它们之间的距离,如何在这4个城市中放置2个ATM,使得城市到ATM的最大距离被最小化。

由于该问题是一个已知的NP难问题,因此没有多项式时间解可用于该问题。有一种多项式时间贪心近似算法,贪心算法提供的解永远不会比最优解差两倍。贪婪的解决方案只有在城市之间的距离跟随时才有效 三角不等式 (两点之间的距离始终小于通过第三点的距离之和)。
2-近似贪婪算法: 1) 任意选择第一个中心。 2) 使用以下标准选择剩余的k-1中心。 让c1,c2,c3,…ci成为已经选择的中心。选择 (i+1)选择距离现在最远的城市作为第四个中心 选定的中心,即点p,其最大值如下: 最小[距离(p,c1),距离(p,c2),距离(p,c3),…距离(p,ci)]
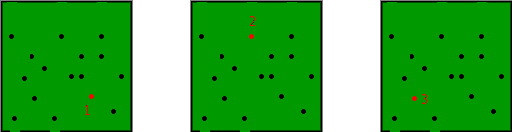
示例(上图中k=3) a) 让第一个任意拾取的顶点为0。 b) 下一个顶点是1,因为1是距离0最远的顶点。 c) 剩下的城市分别是2号和3号。计算它们与已选定中心(0和1)的距离。贪婪算法基本上计算以下值。 从2个中心到已考虑中心的最小距离 最小[dist(2,0),dist(2,1)]=Min[7,8]=7 从3个中心到已考虑中心的最小距离 最小值[dist(3,0),dist(3,1)]=Min[6,5]=5 计算上述值后,选择城市2,因为对应于2的值最大。
请注意,贪心算法不会给出k=2的最佳解,因为这只是一个近似算法,其界为两倍最优。
证明了上述贪婪算法是2近似的。 设OPT为最优解中城市与中心的最大距离。我们需要证明贪婪算法得到的最大距离是2*OPT。 可以用矛盾来证明。 a) 假设从最远点到所有中心的距离>2.OPT。 b) 这意味着所有中心之间的距离也大于2。 c) 我们有k+1点,每对之间的距离>2·OPT。 d) 每个点都有一个最优解的中心,距离<=OPT。 e) 最优解中存在一对中心X相同的点(鸽子洞原理:k个最优中心,k+1点) f) 它们之间的距离最多为2·OPT(三角形不等式),这是一个矛盾。
C++
// C++ program for the above approach #include <bits/stdc++.h> using namespace std; int maxindex( int * dist, int n) { int mi = 0; for ( int i = 0; i < n; i++) { if (dist[i] > dist[mi]) mi = i; } return mi; } void selectKcities( int n, int weights[4][4], int k) { int * dist = new int [n]; vector< int > centers; for ( int i = 0; i < n; i++) { dist[i] = INT_MAX; } // index of city having the // maximum distance to it's // closest center int max = 0; for ( int i = 0; i < k; i++) { centers.push_back(max); for ( int j = 0; j < n; j++) { // updating the distance // of the cities to their // closest centers dist[j] = min(dist[j], weights[max][j]); } // updating the index of the // city with the maximum // distance to it's closest center max = maxindex(dist, n); } // Printing the maximum distance // of a city to a center // that is our answer cout << endl << dist[max] << endl; // Printing the cities that // were chosen to be made // centers for ( int i = 0; i < centers.size(); i++) { cout << centers[i] << " " ; } cout << endl; } // Driver Code int main() { int n = 4; int weights[4][4] = { { 0, 4, 8, 5 }, { 4, 0, 10, 7 }, { 8, 10, 0, 9 }, { 5, 7, 9, 0 } }; int k = 2; // Function Call selectKcities(n, weights, k); } // Contributed by Balu Nagar |
JAVA
// Java program for the above approach import java.util.*; class GFG{ static int maxindex( int [] dist, int n) { int mi = 0 ; for ( int i = 0 ; i < n; i++) { if (dist[i] > dist[mi]) mi = i; } return mi; } static void selectKcities( int n, int weights[][], int k) { int [] dist = new int [n]; ArrayList<Integer> centers = new ArrayList<>(); for ( int i = 0 ; i < n; i++) { dist[i] = Integer.MAX_VALUE; } // Index of city having the // maximum distance to it's // closest center int max = 0 ; for ( int i = 0 ; i < k; i++) { centers.add(max); for ( int j = 0 ; j < n; j++) { // Updating the distance // of the cities to their // closest centers dist[j] = Math.min(dist[j], weights[max][j]); } // Updating the index of the // city with the maximum // distance to it's closest center max = maxindex(dist, n); } // Printing the maximum distance // of a city to a center // that is our answer System.out.println(dist[max]); // Printing the cities that // were chosen to be made // centers for ( int i = 0 ; i < centers.size(); i++) { System.out.print(centers.get(i) + " " ); } System.out.print( "" ); } // Driver Code public static void main(String[] args) { int n = 4 ; int [][] weights = new int [][]{ { 0 , 4 , 8 , 5 }, { 4 , 0 , 10 , 7 }, { 8 , 10 , 0 , 9 }, { 5 , 7 , 9 , 0 } }; int k = 2 ; // Function Call selectKcities(n, weights, k); } } // This code is contributed by nspatilme |
Python3
# Python3 program for the above approach def maxindex(dist, n): mi = 0 for i in range (n): if (dist[i] > dist[mi]): mi = i return mi def selectKcities(n, weights, k): dist = [ 0 ] * n centers = [] for i in range (n): dist[i] = 10 * * 9 # index of city having the # maximum distance to it's # closest center max = 0 for i in range (k): centers.append( max ) for j in range (n): # updating the distance # of the cities to their # closest centers dist[j] = min (dist[j], weights[ max ][j]) # updating the index of the # city with the maximum # distance to it's closest center max = maxindex(dist, n) # Printing the maximum distance # of a city to a center # that is our answer # print() print (dist[ max ]) # Printing the cities that # were chosen to be made # centers for i in centers: print (i, end = " " ) # Driver Code if __name__ = = '__main__' : n = 4 weights = [ [ 0 , 4 , 8 , 5 ], [ 4 , 0 , 10 , 7 ], [ 8 , 10 , 0 , 9 ], [ 5 , 7 , 9 , 0 ] ] k = 2 # Function Call selectKcities(n, weights, k) # This code is contributed by mohit kumar 29. |
C#
using System; using System.Collections.Generic; public class GFG{ static int maxindex( int [] dist, int n) { int mi = 0; for ( int i = 0; i < n; i++) { if (dist[i] > dist[mi]) mi = i; } return mi; } static void selectKcities( int n, int [,] weights, int k) { int [] dist = new int [n]; List< int > centers = new List< int >(); for ( int i = 0; i < n; i++) { dist[i] = Int32.MaxValue; } // Index of city having the // maximum distance to it's // closest center int max = 0; for ( int i = 0; i < k; i++) { centers.Add(max); for ( int j = 0; j < n; j++) { // Updating the distance // of the cities to their // closest centers dist[j] = Math.Min(dist[j], weights[max,j]); } // Updating the index of the // city with the maximum // distance to it's closest center max = maxindex(dist, n); } // Printing the maximum distance // of a city to a center // that is our answer Console.WriteLine(dist[max]); // Printing the cities that // were chosen to be made // centers for ( int i = 0; i < centers.Count; i++) { Console.Write(centers[i] + " " ); } Console.Write( "" ); } // Driver Code static public void Main (){ int n = 4; int [,] weights = new int [,]{ { 0, 4, 8, 5 }, { 4, 0, 10, 7 }, { 8, 10, 0, 9 }, { 5, 7, 9, 0 } }; int k = 2; // Function Call selectKcities(n, weights, k); } } // This code is contributed by avanitrachhadiya2155. |
Javascript
<script> // Javascript program for the above approach function maxindex(dist,n) { let mi = 0; for (let i = 0; i < n; i++) { if (dist[i] > dist[mi]) mi = i; } return mi; } function selectKcities(n,weights,k) { let dist = new Array(n); let centers = []; for (let i = 0; i < n; i++) { dist[i] = Number.MAX_VALUE; } // Index of city having the // maximum distance to it's // closest center let max = 0; for (let i = 0; i < k; i++) { centers.push(max); for (let j = 0; j < n; j++) { // Updating the distance // of the cities to their // closest centers dist[j] = Math.min(dist[j], weights[max][j]); } // Updating the index of the // city with the maximum // distance to it's closest center max = maxindex(dist, n); } // Printing the maximum distance // of a city to a center // that is our answer document.write(dist[max]+ "<br>" ); // Printing the cities that // were chosen to be made // centers for (let i = 0; i < centers.length; i++) { document.write(centers[i] + " " ); } document.write( "<br>" ); } // Driver Code let n = 4; let weights = [ [ 0, 4, 8, 5 ], [ 4, 0, 10, 7 ], [ 8, 10, 0, 9 ], [ 5, 7, 9, 0 ] ] let k = 2 selectKcities(n, weights, k) // This code is contributed by unknown2108 </script> |
50 2
资料来源: http://algo2.iti.kit.edu/vanstee/courses/kcenter.pdf 本文由 严厉的 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



