马纳彻算法——线性时间最长回文子串——第1部分

给定一个字符串，找到最长的回文子字符串。

• 如果给定的字符串是“ForgekskeegFor”，则输出应该是“Geekskeeg”
• 如果给定的字符串是“abaaba”，则输出应该是“abaaba”
• 如果给定字符串为“abababa”，则输出应为“abababa”
• 如果给定字符串为“abcbabcba”，则输出应为“abcbabcba”

我们已经讨论过天真[O（n）] ^3. )]和二次[O（n ^2. )]接近 第一组 和 第二组 . 在本文中，我们将讨论 马纳彻算法 找到线性时间内最长的回文子串。 单向( 第二组 )找到回文就是从字符串的中心开始，逐个比较两个方向上的字符。如果两侧（中间的左侧和右侧）的对应字符匹配，则它们将构成回文。 让我们考虑字符串“abababa”。 这里字符串的中心是第四个字符（索引为3）b。如果我们匹配中心左右的字符，所有字符都匹配，所以字符串“abababa”是一个回文。

这里的中心位置不仅是实际的字符串位置，还可以是两个字符之间的位置。 考虑偶数长度的字符串“ABAABA”。该字符串分别位于第3和第4个字符a和a之间。

要找到长度为N的字符串的最长回文子串，一种方法是取每个可能的2*N+1中心（N个字符位置，两个字符位置之间的N-1和左右两端的2个位置），在每个2*N+1中心的左右方向上进行字符匹配，并跟踪LPS。这种方法需要O（N^2）个时间，这就是我们现在正在做的 第二组 .

让我们考虑两个字符串“abababa”和“ababa”，如下所示：

在这两个弦中，中心位置的左侧和右侧（第一弦中的位置7和第二弦中的位置6）是对称的。为什么？因为整个字符串是围绕中心位置的回文。 如果我们需要从左到右计算每个2*N+1位置的最长回文子串，那么回文的对称属性可以帮助避免一些不必要的计算（即字符比较）。如果有一个长度为L的回文位于任意位置P的中心，那么我们可能不需要比较位置P+1左右两侧的所有字符。我们已经计算了P位之前的LPS，它们可以帮助避免P位之后的一些比较。 这种在以后时间点使用以前位置的信息使得马纳彻算法线性化。在 第二组 ，没有重用以前的信息，因此这是二次的。

马纳彻的算法可能被认为很难理解，所以这里我们将尽可能详细地讨论它。其中一些部分可能需要多次阅读才能正确理解。

让我们看看字符串“abababa”。上图3显示了15个中心位置。我们需要计算每个位置最长回文字符串的长度。

• 在位置0处，根本没有LPS（左侧没有可比较的字符），所以LPS的长度将为0。
• 在位置1，LPS为a，所以LPS的长度为1。
• 在位置2，根本没有LPS（左右字符a和b不匹配），所以LPS的长度将为0。
• 在位置3，LPS是aba，所以LPS的长度是3。
• 在位置4，根本没有LPS（左右字符b和a不匹配），所以LPS的长度将为0。
• 在第5位，LPS的长度是5。

……等等

我们将所有这些回文长度存储在一个数组中，比如L。然后字符串S和LPS长度L如下所示：

类似地，字符串“abaaba”的LPS长度L将如下所示：

在LPS数组L中：

• 奇数位置（实际字符位置）的LPS长度值将为奇数且大于或等于1（如果左侧和右侧没有其他匹配项，则1将来自中心字符本身）
• 偶数位置的LPS长度值（两个字符之间的位置，最左和最右位置）将为偶数且大于或等于0（当左右侧不匹配时，将出现0）

字符串的位置和索引在这里是两个不同的东西。对于长度为N的给定字符串S，索引将从0到N-1（总共N个索引），位置将从0到2*N（总共2*N+1个位置）。

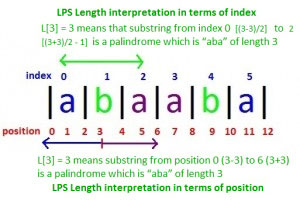
LPS长度值可以用两种方式解释，一种是根据指数，另一种是根据位置。位置I处的LPS值d（L[I]=d）表示：

• 从位置i-d到i+d的子串是长度为d的回文（根据位置）
• 从索引（i-d）/2到[（i+d）/2–1]的子串是长度为d的回文（就索引而言）

e、 g.在字符串“abaaba”中，L[3]=3意味着从位置0（3-3）到6（3+3）的子串是长度为3的回文“aba”，也意味着从索引0[（3-3）/2]到2[（3+3）/2–1]的子串是长度为3的回文“aba”。

现在的主要任务是高效地计算LPS阵列。一旦计算出这个数组，字符串S的LPS将集中在LPS长度值最大的位置。 我们将在未来看到它 第二部分 .

本文由 导演 。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请发表评论。