给定一个二叉树和两个级别的数字“low”和“high”,从低级到高级打印节点。
null
For example consider the binary tree given in below diagram. Input: Root of below tree, low = 2, high = 4Output:8 224 1210 14
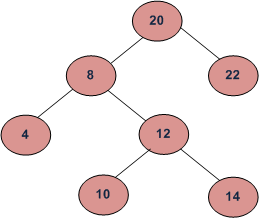
A. 简单方法 首先编写一个递归函数,打印给定级别的节点。然后在循环中从低到高调用递归函数。该方法的时间复杂度为O(n) 2. ) 我们可以打印节点 在O(n)时间内 使用基于队列的迭代级顺序遍历。其思想是进行简单的基于队列的级别顺序遍历。在进行有序遍历时,在末尾添加一个标记节点。每当我们看到一个标记节点,我们就会增加级别数。如果级别编号介于低和高之间,则打印节点。 以下是上述想法的实施。
C++
// A C++ program to print Nodes level by level between given two levels. #include <bits/stdc++.h> using namespace std; /* A binary tree Node has key, pointer to left and right children */ struct Node { int key; struct Node* left, *right; }; /* Given a binary tree, print nodes from level number 'low' to level number 'high'*/ void printLevels(Node* root, int low, int high) { queue <Node *> Q; Node *marker = new Node; // Marker node to indicate end of level int level = 1; // Initialize level number // Enqueue the only first level node and marker node for end of level Q.push(root); Q.push(marker); // Simple level order traversal loop while (Q.empty() == false ) { // Remove the front item from queue Node *n = Q.front(); Q.pop(); // Check if end of level is reached if (n == marker) { // print a new line and increment level number cout << endl; level++; // Check if marker node was last node in queue or // level number is beyond the given upper limit if (Q.empty() == true || level > high) break ; // Enqueue the marker for end of next level Q.push(marker); // If this is marker, then we don't need print it // and enqueue its children continue ; } // If level is equal to or greater than given lower level, // print it if (level >= low) cout << n->key << " " ; // Enqueue children of non-marker node if (n->left != NULL) Q.push(n->left); if (n->right != NULL) Q.push(n->right); } } /* Helper function that allocates a new Node with the given key and NULL left and right pointers. */ Node* newNode( int key) { Node* temp = new Node; temp->key = key; temp->left = temp->right = NULL; return (temp); } /* Driver program to test above functions*/ int main() { // Let us construct the BST shown in the above figure struct Node *root = newNode(20); root->left = newNode(8); root->right = newNode(22); root->left->left = newNode(4); root->left->right = newNode(12); root->left->right->left = newNode(10); root->left->right->right = newNode(14); cout << "Level Order traversal between given two levels is" ; printLevels(root, 2, 3); return 0; } |
JAVA
// Java program to print Nodes level by level between given two levels import java.util.LinkedList; import java.util.Queue; /* A binary tree Node has key, pointer to left and right children */ class Node { int data; Node left, right; public Node( int item) { data = item; left = right = null ; } } class BinaryTree { Node root; /* Given a binary tree, print nodes from level number 'low' to level number 'high'*/ void printLevels(Node node, int low, int high) { Queue<Node> Q = new LinkedList<>(); Node marker = new Node( 4 ); // Marker node to indicate end of level int level = 1 ; // Initialize level number // Enqueue the only first level node and marker node for end of level Q.add(node); Q.add(marker); // Simple level order traversal loop while (Q.isEmpty() == false ) { // Remove the front item from queue Node n = Q.peek(); Q.remove(); // Check if end of level is reached if (n == marker) { // print a new line and increment level number System.out.println( "" ); level++; // Check if marker node was last node in queue or // level number is beyond the given upper limit if (Q.isEmpty() == true || level > high) break ; // Enqueue the marker for end of next level Q.add(marker); // If this is marker, then we don't need print it // and enqueue its children continue ; } // If level is equal to or greater than given lower level, // print it if (level >= low) System.out.print( n.data + " " ); // Enqueue children of non-marker node if (n.left != null ) Q.add(n.left); if (n.right != null ) Q.add(n.right); } } // Driver program to test for above functions public static void main(String args[]) { BinaryTree tree = new BinaryTree(); tree.root = new Node( 20 ); tree.root.left = new Node( 8 ); tree.root.right = new Node( 22 ); tree.root.left.left = new Node( 4 ); tree.root.left.right = new Node( 12 ); tree.root.left.right.left = new Node( 10 ); tree.root.left.right.right = new Node( 14 ); System.out.print( "Level Order traversal between given two levels is " ); tree.printLevels(tree.root, 2 , 3 ); } } // This code has been contributed by Mayank Jaiswal |
Python3
# Python program to print nodes level by level between # given two levels # A binary tree node class Node: # Constructor to create a new node def __init__( self , key): self .key = key self .left = None self .right = None # Given a binary tree, print nodes form level number 'low' # to level number 'high' def printLevels(root, low, high): Q = [] marker = Node( 11114 ) # Marker node to indicate end of level level = 1 # Initialize level number # Enqueue the only first level node and marker node for # end of level Q.append(root) Q.append(marker) #print Q # Simple level order traversal loop while ( len (Q) > 0 ): # Remove the front item from queue n = Q[ 0 ] Q.pop( 0 ) #print Q # Check if end of level is reached if n = = marker: # print a new line and increment level number print () level + = 1 # Check if marker node was last node in queue # or level number is beyond the given upper limit if len (Q) = = 0 or level > high: break # Enqueue the marker for end of next level Q.append(marker) # If this is marker, then we don't need print it # and enqueue its children continue if level > = low: print (n.key,end = " " ) # Enqueue children of non-marker node if n.left is not None : Q.append(n.left) Q.append(n.right) # Driver program to test the above function root = Node( 20 ) root.left = Node( 8 ) root.right = Node( 22 ) root.left.left = Node( 4 ) root.left.right = Node( 12 ) root.left.right.left = Node( 10 ) root.left.right.right = Node( 14 ) print ( "Level Order Traversal between given two levels is" ,printLevels(root, 2 , 3 )) # This code is contributed by Nikhil Kumar Singh(nickzuck_007) |
C#
using System; using System.Collections.Generic; // c# program to print Nodes level by level between given two levels /* A binary tree Node has key, pointer to left and right children */ public class Node { public int data; public Node left, right; public Node( int item) { data = item; left = right = null ; } } public class BinaryTree { public Node root; /* Given a binary tree, print nodes from level number 'low' to level number 'high'*/ public virtual void printLevels(Node node, int low, int high) { LinkedList<Node> Q = new LinkedList<Node>(); Node marker = new Node(4); // Marker node to indicate end of level int level = 1; // Initialize level number // Enqueue the only first level node and marker node for end of level Q.AddLast(node); Q.AddLast(marker); // Simple level order traversal loop while (Q.Count > 0) { // Remove the front item from queue Node n = Q.First.Value; Q.RemoveFirst(); // Check if end of level is reached if (n == marker) { // print a new line and increment level number Console.WriteLine( "" ); level++; // Check if marker node was last node in queue or // level number is beyond the given upper limit if (Q.Count == 0 || level > high) { break ; } // Enqueue the marker for end of next level Q.AddLast(marker); // If this is marker, then we don't need print it // and enqueue its children continue ; } // If level is equal to or greater than given lower level, // print it if (level >= low) { Console.Write(n.data + " " ); } // Enqueue children of non-marker node if (n.left != null ) { Q.AddLast(n.left); } if (n.right != null ) { Q.AddLast(n.right); } } } // Driver program to test for above functions public static void Main( string [] args) { BinaryTree tree = new BinaryTree(); tree.root = new Node(20); tree.root.left = new Node(8); tree.root.right = new Node(22); tree.root.left.left = new Node(4); tree.root.left.right = new Node(12); tree.root.left.right.left = new Node(10); tree.root.left.right.right = new Node(14); Console.Write( "Level Order traversal between given two levels is " ); tree.printLevels(tree.root, 2, 3); } } // This code is contributed by Shrikant13 |
Javascript
<script> // JavaScript program to print Nodes // level by level between given two levels /* A binary tree Node has key, pointer to left and right children */ class Node { constructor(item) { this .data = item; this .left = null ; this .right = null ; } } var root = null ; /* Given a binary tree, print nodes from level number 'low' to level number 'high'*/ function printLevels(node, low, high) { var Q = []; var marker = new Node(4); // Marker node to indicate end of level var level = 1; // Initialize level number // Enqueue the only first level node and // marker node for end of level Q.push(node); Q.push(marker); // Simple level order traversal loop while (Q.length > 0) { // Remove the front item from queue var n = Q[0]; Q.shift(); // Check if end of level is reached if (n == marker) { // print a new line and increment level number document.write( "<br>" ); level++; // Check if marker node was last node in queue or // level number is beyond the given upper limit if (Q.length == 0 || level > high) { break ; } // Enqueue the marker for end of next level Q.push(marker); // If this is marker, then we don't need print it // and enqueue its children continue ; } // If level is equal to or greater than given lower level, // print it if (level >= low) { document.write(n.data + " " ); } // Enqueue children of non-marker node if (n.left != null ) { Q.push(n.left); } if (n.right != null ) { Q.push(n.right); } } } // Driver program to test for above functions root = new Node(20); root.left = new Node(8); root.right = new Node(22); root.left.left = new Node(4); root.left.right = new Node(12); root.left.right.left = new Node(10); root.left.right.right = new Node(14); document.write( "Level Order traversal between given two levels is " ); printLevels(root, 2, 3); </script> |
输出
Level Order traversal between given two levels is8 224 12
上述方法的时间复杂度为O(n),因为它进行简单的水平顺序遍历。
本文由 直率的 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



