找出两个矩形是否重叠-yiteyi-C++库

给定两个矩形，找出给定的两个矩形是否重叠。请注意，矩形可以由两个坐标表示，左上角和右下角。所以我们主要得到以下四个坐标。 l1 ：第一个矩形的左上角坐标。 r1 ：第一个矩形的右下角坐标。 l2 ：第二个矩形的左上角坐标。 r2 ：第二个矩形的右下角坐标。

null

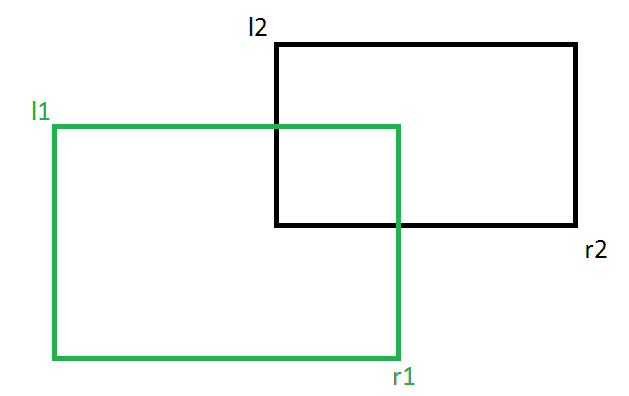
rectanglesOverlap

我们需要写一个函数 布尔·杜弗拉普（l1、r1、l2、r2） 如果两个给定的矩形重叠，则返回true。

建议：请在“上解决” 实践 “首先，在讨论解决方案之前。

注：可以假设矩形平行于坐标轴。一种解决方案是逐个拾取一个矩形的所有点，然后查看该点是否位于另一个矩形内 .这可以使用所讨论的算法来完成在这里 . 下面是一个更简单的方法。两个长方形不要如果下列条件之一为真，则重叠。 1) 一个矩形在另一个矩形的上边缘上方。 2) 一个矩形位于另一个矩形左边缘的左侧。我们需要检查上述情况，以确定给定的矩形是否重叠。以下是上述方法的实现。

C++

                         // CPP program for the above approach                       
                         #include <bits/stdc++.h>                       
           
                         struct                                     Point {                       
                                                 int                                     x, y;                       
                         };                       
           
                         // Returns true if two rectangles (l1, r1) and (l2, r2)                       
                         // overlap                       
                         bool                                     doOverlap(Point l1, Point r1, Point l2, Point r2)                       
                         {                       
           
                                                 // To check if either rectangle is actually a line                       
                                                 // For example :  l1 ={-1,0}  r1={1,1}  l2={0,-1}                       
                                                 // r2={0,1}                       
           
                                                 if                                     (l1.x == r1.x || l1.y == r1.y || l2.x == r2.x                       
                                                 || l2.y == r2.y) {                       
                                                 // the line cannot have positive overlap                       
                                                 return                                     false                                     ;                       
                                                 }                       
           
                                                 // If one rectangle is on left side of other                       
                                                 if                                     (l1.x >= r2.x || l2.x >= r1.x)                       
                                                 return                                     false                                     ;                       
           
                                                 // If one rectangle is above other                       
                                                 if                                     (r1.y >= l2.y || r2.y >= l1.y)                       
                                                 return                                     false                                     ;                       
           
                                                 return                                     true                                     ;                       
                         }                       
           
                         /* Driver program to test above function */                       
                         int                                     main()                       
                         {                       
                                                 Point l1 = { 0, 10 }, r1 = { 10, 0 };                       
                                                 Point l2 = { 5, 5 }, r2 = { 15, 0 };                       
                                                 if                                     (doOverlap(l1, r1, l2, r2))                       
                                                 printf                                     (                                     "Rectangles Overlap"                                     );                       
                                                 else                       
                                                 printf                                     (                                     "Rectangles Don't Overlap"                                     );                       
                                                 return                                     0;                       
                         }                       

JAVA

                         // Java program to check if rectangles overlap                       
                         class                                     GFG {                       
           
                                                 static                                     class                                     Point {                       
           
                                                 int                                     x, y;                       
                                                 }                       
           
                         // Returns true if two rectangles (l1, r1) and (l2, r2) overlap                       
                                                 static                                     boolean                                     doOverlap(Point l1, Point r1, Point l2, Point r2) {                       
                                   
                                                 // To check if either rectangle is actually a line                       
                                                 // For example :  l1 ={-1,0}  r1={1,1}  l2={0,-1}  r2={0,1}                       
                                   
                                                 if                                     (l1.x == r1.x || l1.y == r1.y || l2.x == r2.x || l2.y == r2.y)                       
                                                 {                       
                                                 // the line cannot have positive overlap                       
                                                 return                                     false                                     ;                       
                                                 }                       
                                   
                                   
                                                 // If one rectangle is on left side of other                       
                                                 if                                     (l1.x >= r2.x || l2.x >= r1.x) {                       
                                                 return                                     false                                     ;                       
                                                 }                       
           
                                                 // If one rectangle is above other                       
                                                 if                                     (r1.y >= l2.y || r2.y >= l1.y) {                       
                                                 return                                     false                                     ;                       
                                                 }                       
           
                                                 return                                     true                                     ;                       
                                                 }                       
           
                                                 /* Driver program to test above function */                       
                                                 public                                     static                                     void                                     main(String[] args) {                       
                                                 Point l1 =                                     new                                     Point(),r1 =                                     new                                     Point(),                       
                                                 l2 =                                     new                                     Point(),r2 =                                     new                                     Point();                       
                                                 l1.x=                                     0                                     ;l1.y=                                     10                                     ; r1.x=                                     10                                     ;r1.y=                                     0                                     ;                       
                                                 l2.x=                                     5                                     ;l2.y=                                     5                                     ; r2.x=                                     15                                     ;r2.y=                                     0                                     ;                       
           
                                                 if                                     (doOverlap(l1, r1, l2, r2)) {                       
                                                 System.out.println(                                     "Rectangles Overlap"                                     );                       
                                                 }                                     else                                     {                       
                                                 System.out.println(                                     "Rectangles Don't Overlap"                                     );                       
                                                 }                       
                                                 }                       
                         }                       
                         //this code contributed by PrinciRaj1992                       

Python3

                         # Python program to check if rectangles overlap                       
                         class                                     Point:                       
                                                 def                                     __init__(                                     self                                     , x, y):                       
                                                 self                                     .x                                     =                                     x                       
                                                 self                                     .y                                     =                                     y                       
           
                         # Returns true if two rectangles(l1, r1)                       
                         # and (l2, r2) overlap                       
                         def                                     doOverlap(l1, r1, l2, r2):                       
                                   
                                                 # To check if either rectangle is actually a line                       
                                                 # For example  :  l1 ={-1,0}  r1={1,1}  l2={0,-1}  r2={0,1}                       
                                   
                                                 if                                     (l1.x                                     =                                     =                                     r1.x                                     or                                     l1.y                                     =                                     =                                     r1.y                                     or                                     l2.x                                     =                                     =                                     r2.x                                     or                                     l2.y                                     =                                     =                                     r2.y):                       
                                                 # the line cannot have positive overlap                       
                                                 return                                     False                       
                                   
                                   
                                                 # If one rectangle is on left side of other                       
                                                 if                                     (l1.x >                                     =                                     r2.x                                     or                                     l2.x >                                     =                                     r1.x):                       
                                                 return                                     False                       
           
                                                 # If one rectangle is above other                       
                                                 if                                     (r1.y >                                     =                                     l2.y                                     or                                     r2.y >                                     =                                     l1.y):                       
                                                 return                                     False                       
           
                                                 return                                     True                       
           
                         # Driver Code                       
                         if                                     __name__                                     =                                     =                                     "__main__"                                     :                       
                                                 l1                                     =                                     Point(                                     0                                     ,                                     10                                     )                       
                                                 r1                                     =                                     Point(                                     10                                     ,                                     0                                     )                       
                                                 l2                                     =                                     Point(                                     5                                     ,                                     5                                     )                       
                                                 r2                                     =                                     Point(                                     15                                     ,                                     0                                     )                       
           
                                                 if                                     (doOverlap(l1, r1, l2, r2)):                       
                                                 print                                     (                                     "Rectangles Overlap"                                     )                       
                                                 else                                     :                       
                                                 print                                     (                                     "Rectangles Don't Overlap"                                     )                       
           
                         # This code is contributed by Vivek Kumar Singh                       

C#

                         // C# program to check if rectangles overlap                       
                         using                                     System;                       
                                   
                         class                                     GFG                       
                         {                       
                                                 class                                     Point                       
                                                 {                       
                                                 public                                     int                                     x, y;                       
                                                 }                       
           
                                                 // Returns true if two rectangles (l1, r1)                       
                                                 // and (l2, r2) overlap                       
                                                 static                                     bool                                     doOverlap(Point l1, Point r1,                       
                                                 Point l2, Point r2)                       
                                                 {                       
                                                 // If one rectangle is on left side of other                       
                                                 if                                     (l1.x >= r2.x || l2.x >= r1.x)                       
                                                 {                       
                                                 return                                     false                                     ;                       
                                                 }                       
           
                                                 // If one rectangle is above other                       
                                                 if                                     (r1.y >= l2.y || r2.y >= l1.y)                       
                                                 {                       
                                                 return                                     false                                     ;                       
                                                 }                       
                                                 return                                     true                                     ;                       
                                                 }                       
           
                                                 // Driver Code                       
                                                 public                                     static                                     void                                     Main()                       
                                                 {                       
                                                 Point l1 =                                     new                                     Point(), r1 =                                     new                                     Point(),                       
                                                 l2 =                                     new                                     Point(), r2 =                                     new                                     Point();                       
                                                 l1.x = 0;l1.y = 10; r1.x = 10;r1.y = 0;                       
                                                 l2.x = 5;l2.y = 5; r2.x = 15;r2.y = 0;                       
                                                 if                                     (doOverlap(l1, r1, l2, r2))                       
                                                 {                       
                                                 Console.WriteLine(                                     "Rectangles Overlap"                                     );                       
                                                 }                                     else                       
                                                 {                       
                                                 Console.WriteLine(                                     "Rectangles Don't Overlap"                                     );                       
                                                 }                       
                                                 }                       
                         }                       
           
                         // This code is contributed by                       
                         // Rajput-Ji                       

Javascript

                         <script>                       
           
                         // JavaScript program to check if rectangles overlap                       
                         class Point {                       
           
                                                 constructor(val) {                       
                                                 this                                     .x = val;                       
                                                 this                                     .y = val;                       
                                                 }                       
                                                 }                       
           
                                                 // Returns true if two rectangles                       
                                                 // (l1, r1) and (l2, r2) overlap                       
                                                 function                                     doOverlap( l1,  r1,  l2,  r2) {                       
           
                                                 // To check if either rectangle is actually a line                       
                                                 // For example : l1 ={-1,0} r1={1,1} l2={0,-1} r2={0,1}                       
           
                                                 if                                     (l1.x == r1.x || l1.y == r1.y ||                       
                                                 l2.x == r2.x || l2.y == r2.y) {                       
                                                 // the line cannot have positive overlap                       
                                                 return                                     false                                     ;                       
                                                 }                       
           
                                                 // If one rectangle is on left side of other                       
                                                 if                                     (l1.x >= r2.x || l2.x >= r1.x) {                       
                                                 return                                     false                                     ;                       
                                                 }                       
           
                                                 // If one rectangle is above other                       
                                                 if                                     (r1.y >= l2.y || r2.y >= l1.y) {                       
                                                 return                                     false                                     ;                       
                                                 }                       
           
                                                 return                                     true                                     ;                       
                                                 }                       
           
                                                 /* Driver program to test above function */                       
                                   
                                                 var                                     l1 =                                     new                                     Point(), r1 =                                     new                                     Point(),                       
                                                 l2 =                                     new                                     Point(), r2 =                                     new                                     Point();                       
                                                 l1.x = 0;                       
                                                 l1.y = 10;                       
                                                 r1.x = 10;                       
                                                 r1.y = 0;                       
                                                 l2.x = 5;                       
                                                 l2.y = 5;                       
                                                 r2.x = 15;                       
                                                 r2.y = 0;                       
           
                                                 if                                     (doOverlap(l1, r1, l2, r2)) {                       
                                                 document.write(                                     "Rectangles Overlap"                                     );                       
                                                 }                                     else                                     {                       
                                                 document.write(                                     "Rectangles Don't Overlap"                                     );                       
                                                 }                       
           
                         // This code contributed by umadevi9616                       
           
                         </script>                       

输出

Rectangles Overlap

上述代码的时间复杂度为O（1），因为代码没有任何循环或递归。

辅助空间： O（1）

本文由 阿曼·古普塔 。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请发表评论。

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章