所有对最短路径的Johnson算法

问题是在给定的加权有向图中寻找每对顶点之间的最短路径，并且权重可能为负。我们讨论过 弗洛伊德·沃沙尔算法 对于这个问题。Floyd-Warshall算法的时间复杂度为Θ（V） ^3. ). 利用Johnson算法，我们可以找到O（V）中的所有对最短路径 ^2. 记录（V+VE）时间。 约翰逊的算法同时使用了这两种方法 迪杰斯特拉 和 距离向量 作为子程序。

如果我们申请 Dijkstra的单源最短路径算法 对于每个顶点，将每个顶点视为源，我们可以在O（V*VLogV）时间内找到所有对最短路径。因此，使用Dijkstra的单源最短路径似乎比 弗洛伊德·沃谢尔 ，但Dijkstra算法的问题是，它不适用于负权重边。 约翰逊算法的思想是重新加权所有边，使它们都为正，然后对每个顶点应用Dijkstra算法。

如何将给定的图转换为具有所有非负权边的图？ 人们可能会想到一种简单的方法，找到最小权重边，并将此权重添加到所有边上。不幸的是，这不起作用，因为在不同的路径中可能有不同数量的边（请参见） 这 例如）。如果从一个顶点u到v有多条路径，那么所有路径都必须以相同的数量增加，以便最短路径在变换后的图中保持最短。 约翰逊算法的思想是给每个顶点分配一个权重。指定顶点权重[u]。我们使用顶点权重重新加权边。例如，对于权重为w（u，v）的边（u，v），新权重将变为w（u，v）+h[u]–h[v]。这种重新加权的好处是，任意两个顶点之间的所有路径集都以相同的数量增加，所有负权重都变为非负。考虑两个顶点S和T之间的任何路径，每个路径的权重由H[s]-H[t]增加，路径上的顶点的所有H[]值从S到T彼此抵消。

我们如何计算h[]值？ 贝尔曼-福特算法 用于此目的。下面是完整的算法。将向图形中添加一个新顶点，并将其连接到所有现有顶点。从新顶点到所有现有顶点的最短距离值为h[]值。

算法： 1) 设给定的图为G。向图中添加一个新顶点s，将新顶点的边添加到G的所有顶点。设修改后的图为G’。

2) 跑 贝尔曼-福特算法 以s为源的G。设Bellman Ford计算的距离为h[0]，h[1]。。h[V-1]。如果我们发现一个负的重量循环，然后返回。请注意，新顶点s无法创建负权重循环，因为没有到s的边。所有边都来自s。

3) 重新加权原始图形的边。对于每条边（u，v），将新权重指定为“原始权重+h[u]–h[v]”。

4) 移除添加的顶点s并运行 Dijkstra算法 对于每个顶点。

转换如何确保非负权重边？ 以下属性始终适用于h[]值，因为它们是最短距离。

   h[v] <= h[u] + w(u, v) 

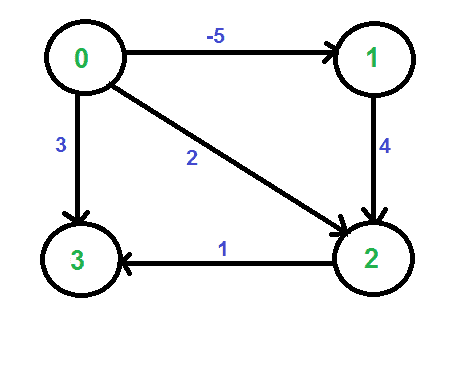
该属性的简单意思是，从s到v的最短距离必须小于或等于从s到u的最短距离加上边的权重（u，v）。新的权重为w（u，v）+h[u]-h[v]。由于不等式“h[v]<=h[u]+w（u，v）”，新权重的值必须大于或等于零。 例子： 让我们考虑下面的图表。

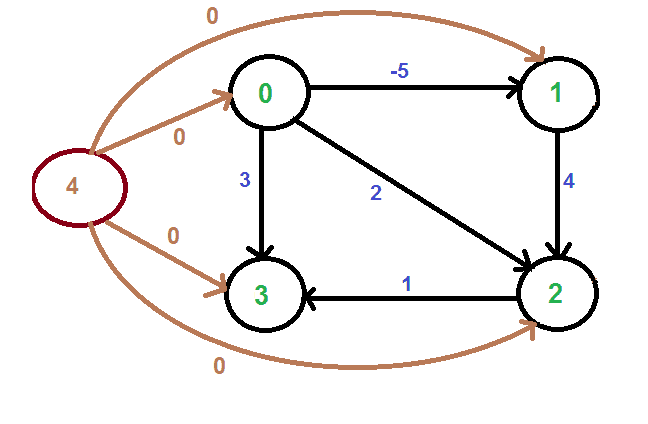
我们添加一个源s，并将s的边添加到原始图的所有顶点。在下图中，s是4。

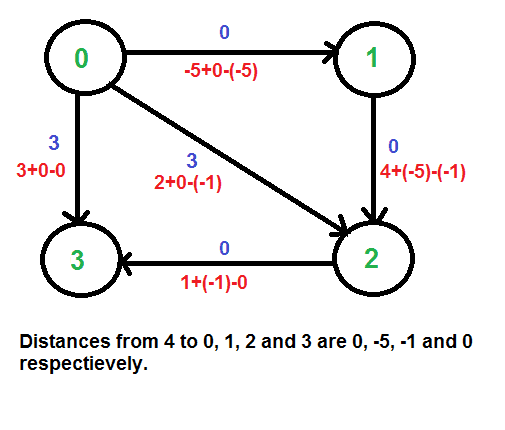
我们使用Bellman-Ford算法计算从4到所有其他顶点的最短距离。从4到0、1、2和3的最短距离分别为0、-5、-1和0，即h[]={0、-5、-1、0}。得到这些距离后，我们移除源顶点4，并使用以下公式重新加权边。w（u，v）=w（u，v）+h[u]-h[v]。

因为现在所有的权重都是正的，所以我们可以对每个顶点运行Dijkstra的最短路径算法作为源。

时间复杂性： 算法的主要步骤是Bellman-Ford算法，称为once，Dijkstra算法称为V-times。Bellman Ford的时间复杂度为O（VE），Dijkstra的时间复杂度为O（VLogV）。所以总的时间复杂度是O（V） ^2. 对数V+VE）。 约翰逊算法的时间复杂度与 弗洛伊德·沃谢尔 当图是完整的（对于完整的图E=O（V ^2. ).但对于稀疏图，该算法的性能比 弗洛伊德·沃谢尔 .

参考资料： 算法导论第三版由Clifford Stein、Thomas H.Cormen、Charles E.Leiserson、Ronald L.Rivest编写 http://www.youtube.com/watch?v=b6LOHvCzmkI http://www.youtube.com/watch?v=TV2Z6nbo1ic http://en.wikipedia.org/wiki/Johnson%27s_algorithm http://www.youtube.com/watch?v=Sygq1e0xWnM

如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。