考虑一行n个硬币的值v1…vn,其中n是偶数。我们轮流与对手比赛。在每一轮中,玩家从该行中选择第一枚或最后一枚硬币,将其永久性地从该行中移除,并获得硬币的价值。确定如果我们先行动,我们肯定能赢得的最大可能金额。 注意:对手和用户一样聪明。
null
让我们用几个例子来理解这个问题:
- 5,3,7,10:用户收集的最大值为15(10+5)
- 8,15,3,7:用户收集的最大值为22(7+15)
在每一步中选择最好的,是否会给出最佳解决方案?不 在第二个例子中,游戏可以这样结束:
- …….用户选择8。 …….对手选择15人。 …….用户选择7。 …….对手选择3。 用户收集的总价值为15(8+7)
- …….用户选择7。 …….对手选择8。 …….用户选择15个。 …….对手选择3。 用户收集的总价值为22(7+15)
因此,如果用户遵循第二个游戏状态,则可以收集最大值,尽管第一步不是最好的。
方法: 由于两名球员都同样强大,双方都会努力降低对方获胜的可能性。现在让我们看看对手是如何做到这一点的。
有两种选择:
- 用户选择值为“Vi”的第i个硬币:对手选择第(i+1)个硬币或第j个硬币。对手打算选择留给用户的硬币 最小值 . i、 e.用户可以收集值 Vi+min(F(i+2,j),F(i+1,j-1)) .
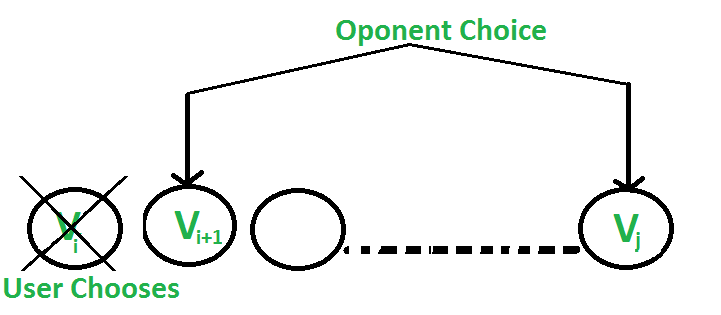
- 用户选择价值为“Vj”的“第j个”硬币:对手选择“第i个”或“第(j-1)个”硬币。对手打算选择给用户留下最小价值的硬币,即用户可以收集价值 Vj+min(F(i+1,j-1),F(i,j-2)) .
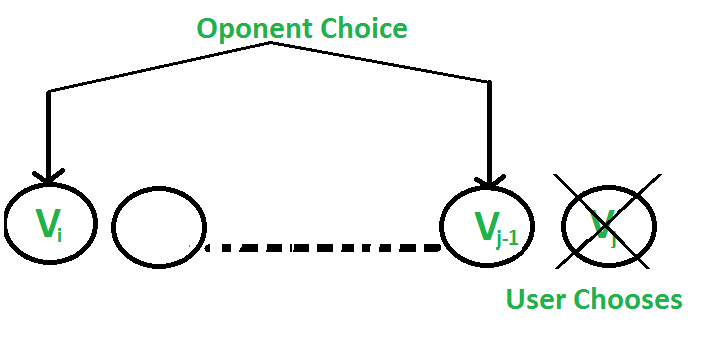
以下是基于上述两种选择的递归解决方案。我们最多有两个选择。
F(i, j) represents the maximum value the usercan collect from i'th coin to j'th coin.F(i, j) = Max(Vi + min(F(i+2, j), F(i+1, j-1) ), Vj + min(F(i+1, j-1), F(i, j-2) ))As user wants to maximise the number of coins. Base Cases F(i, j) = Vi If j == i F(i, j) = max(Vi, Vj) If j == i + 1
C++
// C++ program to find out // maximum value from a given // sequence of coins #include <bits/stdc++.h> using namespace std; // Returns optimal value possible // that a player can collect from // an array of coins of size n. // Note than n must be even int optimalStrategyOfGame( int * arr, int n) { // Create a table to store // solutions of subproblems int table[n][n]; // Fill table using above // recursive formula. Note // that the table is filled // in diagonal fashion (similar // to http:// goo.gl/PQqoS), // from diagonal elements to // table[0][n-1] which is the result. for ( int gap = 0; gap < n; ++gap) { for ( int i = 0, j = gap; j < n; ++i, ++j) { // Here x is value of F(i+2, j), // y is F(i+1, j-1) and // z is F(i, j-2) in above recursive // formula int x = ((i + 2) <= j) ? table[i + 2][j] : 0; int y = ((i + 1) <= (j - 1)) ? table[i + 1][j - 1] : 0; int z = (i <= (j - 2)) ? table[i][j - 2] : 0; table[i][j] = max( arr[i] + min(x, y), arr[j] + min(y, z)); } } return table[0][n - 1]; } // Driver program to test above function int main() { int arr1[] = { 8, 15, 3, 7 }; int n = sizeof (arr1) / sizeof (arr1[0]); printf ( "%d" , optimalStrategyOfGame(arr1, n)); int arr2[] = { 2, 2, 2, 2 }; n = sizeof (arr2) / sizeof (arr2[0]); printf ( "%d" , optimalStrategyOfGame(arr2, n)); int arr3[] = { 20, 30, 2, 2, 2, 10 }; n = sizeof (arr3) / sizeof (arr3[0]); printf ( "%d" , optimalStrategyOfGame(arr3, n)); return 0; } |
JAVA
// Java program to find out maximum // value from a given sequence of coins import java.io.*; class GFG { // Returns optimal value possible // that a player can collect from // an array of coins of size n. // Note than n must be even static int optimalStrategyOfGame( int arr[], int n) { // Create a table to store // solutions of subproblems int table[][] = new int [n][n]; int gap, i, j, x, y, z; // Fill table using above recursive formula. // Note that the tableis filled in diagonal // fashion (similar to http:// goo.gl/PQqoS), // from diagonal elements to table[0][n-1] // which is the result. for (gap = 0 ; gap < n; ++gap) { for (i = 0 , j = gap; j < n; ++i, ++j) { // Here x is value of F(i+2, j), // y is F(i+1, j-1) and z is // F(i, j-2) in above recursive formula x = ((i + 2 ) <= j) ? table[i + 2 ][j] : 0 ; y = ((i + 1 ) <= (j - 1 )) ? table[i + 1 ][j - 1 ] : 0 ; z = (i <= (j - 2 )) ? table[i][j - 2 ] : 0 ; table[i][j] = Math.max( arr[i] + Math.min(x, y), arr[j] + Math.min(y, z)); } } return table[ 0 ][n - 1 ]; } // Driver program public static void main(String[] args) { int arr1[] = { 8 , 15 , 3 , 7 }; int n = arr1.length; System.out.println( "" + optimalStrategyOfGame(arr1, n)); int arr2[] = { 2 , 2 , 2 , 2 }; n = arr2.length; System.out.println( "" + optimalStrategyOfGame(arr2, n)); int arr3[] = { 20 , 30 , 2 , 2 , 2 , 10 }; n = arr3.length; System.out.println( "" + optimalStrategyOfGame(arr3, n)); } } // This code is contributed by vt_m |
Python3
# Python3 program to find out maximum # value from a given sequence of coins # Returns optimal value possible that # a player can collect from an array # of coins of size n. Note than n # must be even def optimalStrategyOfGame(arr, n): # Create a table to store # solutions of subproblems table = [[ 0 for i in range (n)] for i in range (n)] # Fill table using above recursive # formula. Note that the table is # filled in diagonal fashion # (similar to http://goo.gl / PQqoS), # from diagonal elements to # table[0][n-1] which is the result. for gap in range (n): for j in range (gap, n): i = j - gap # Here x is value of F(i + 2, j), # y is F(i + 1, j-1) and z is # F(i, j-2) in above recursive # formula x = 0 if ((i + 2 ) < = j): x = table[i + 2 ][j] y = 0 if ((i + 1 ) < = (j - 1 )): y = table[i + 1 ][j - 1 ] z = 0 if (i < = (j - 2 )): z = table[i][j - 2 ] table[i][j] = max (arr[i] + min (x, y), arr[j] + min (y, z)) return table[ 0 ][n - 1 ] # Driver Code arr1 = [ 8 , 15 , 3 , 7 ] n = len (arr1) print (optimalStrategyOfGame(arr1, n)) arr2 = [ 2 , 2 , 2 , 2 ] n = len (arr2) print (optimalStrategyOfGame(arr2, n)) arr3 = [ 20 , 30 , 2 , 2 , 2 , 10 ] n = len (arr3) print (optimalStrategyOfGame(arr3, n)) # This code is contributed # by sahilshelangia |
C#
// C# program to find out maximum // value from a given sequence of coins using System; public class GFG { // Returns optimal value possible that a player // can collect from an array of coins of size n. // Note than n must be even static int optimalStrategyOfGame( int [] arr, int n) { // Create a table to store solutions of subproblems int [, ] table = new int [n, n]; int gap, i, j, x, y, z; // Fill table using above recursive formula. // Note that the tableis filled in diagonal // fashion (similar to http:// goo.gl/PQqoS), // from diagonal elements to table[0][n-1] // which is the result. for (gap = 0; gap < n; ++gap) { for (i = 0, j = gap; j < n; ++i, ++j) { // Here x is value of F(i+2, j), // y is F(i+1, j-1) and z is // F(i, j-2) in above recursive formula x = ((i + 2) <= j) ? table[i + 2, j] : 0; y = ((i + 1) <= (j - 1)) ? table[i + 1, j - 1] : 0; z = (i <= (j - 2)) ? table[i, j - 2] : 0; table[i, j] = Math.Max(arr[i] + Math.Min(x, y), arr[j] + Math.Min(y, z)); } } return table[0, n - 1]; } // Driver program static public void Main() { int [] arr1 = { 8, 15, 3, 7 }; int n = arr1.Length; Console.WriteLine( "" + optimalStrategyOfGame(arr1, n)); int [] arr2 = { 2, 2, 2, 2 }; n = arr2.Length; Console.WriteLine( "" + optimalStrategyOfGame(arr2, n)); int [] arr3 = { 20, 30, 2, 2, 2, 10 }; n = arr3.Length; Console.WriteLine( "" + optimalStrategyOfGame(arr3, n)); } } // This code is contributed by ajit |
PHP
<?php // PHP program to find out maximum value // from a given sequence of coins // Returns optimal value possible that a // player can collect from an array of // coins of size n. Note than n must be even function optimalStrategyOfGame( $arr , $n ) { // Create a table to store solutions // of subproblems $table = array_fill (0, $n , array_fill (0, $n , 0)); // Fill table using above recursive formula. // Note that the table is filled in diagonal // fashion (similar to http://goo.gl/PQqoS ), // from diagonal elements to table[0][n-1] // which is the result. for ( $gap = 0; $gap < $n ; ++ $gap ) { for ( $i = 0, $j = $gap ; $j < $n ; ++ $i , ++ $j ) { // Here x is value of F(i+2, j), // y is F(i+1, j-1) and z is F(i, j-2) // in above recursive formula $x = (( $i + 2) <= $j ) ? $table [ $i + 2][ $j ] : 0; $y = (( $i + 1) <= ( $j - 1)) ? $table [ $i + 1][ $j - 1] : 0; $z = ( $i <= ( $j - 2)) ? $table [ $i ][ $j - 2] : 0; $table [ $i ][ $j ] = max( $arr [ $i ] + min( $x , $y ), $arr [ $j ] + min( $y , $z )); } } return $table [0][ $n - 1]; } // Driver Code $arr1 = array ( 8, 15, 3, 7 ); $n = count ( $arr1 ); print (optimalStrategyOfGame( $arr1 , $n ) . "" ); $arr2 = array ( 2, 2, 2, 2 ); $n = count ( $arr2 ); print (optimalStrategyOfGame( $arr2 , $n ) . "" ); $arr3 = array (20, 30, 2, 2, 2, 10); $n = count ( $arr3 ); print (optimalStrategyOfGame( $arr3 , $n ) . "" ); // This code is contributed by chandan_jnu ?> |
Javascript
<script> // Javascript program to find out maximum // value from a given sequence of coins // Returns optimal value possible // that a player can collect from // an array of coins of size n. // Note than n must be even function optimalStrategyOfGame(arr, n) { // Create a table to store // solutions of subproblems let table = new Array(n); let gap, i, j, x, y, z; for (let d = 0; d < n; d++) { table[d] = new Array(n); } // Fill table using above recursive formula. // Note that the tableis filled in diagonal // fashion (similar to http:// goo.gl/PQqoS), // from diagonal elements to table[0][n-1] // which is the result. for (gap = 0; gap < n; ++gap) { for (i = 0, j = gap; j < n; ++i, ++j) { // Here x is value of F(i+2, j), // y is F(i+1, j-1) and z is // F(i, j-2) in above recursive formula x = ((i + 2) <= j) ? table[i + 2][j] : 0; y = ((i + 1) <= (j - 1)) ? table[i + 1][j - 1] : 0; z = (i <= (j - 2)) ? table[i][j - 2] : 0; table[i][j] = Math.max( arr[i] + Math.min(x, y), arr[j] + Math.min(y, z)); } } return table[0][n - 1]; } // Driver code let arr1 = [ 8, 15, 3, 7 ]; let n = arr1.length; document.write( "" + optimalStrategyOfGame(arr1, n) + "</br>" ); let arr2 = [ 2, 2, 2, 2 ]; n = arr2.length; document.write( "" + optimalStrategyOfGame(arr2, n) + "</br>" ); let arr3 = [ 20, 30, 2, 2, 2, 10 ]; n = arr3.length; document.write( "" + optimalStrategyOfGame(arr3, n)); // This code is contributed by divyesh072019 </script> |
输出:
22442
复杂性分析:
- 时间复杂性: O(n) 2. ). 使用嵌套for循环将时间复杂度提高到n 2. .
- 辅助空间: O(n) 2. ). 因为二维表格用于存储状态。
注: 上述解决方案可以通过减少每次选择的比较次数来优化。请参阅下文。 游戏的最优策略|集2
练习: 当用户希望只赢而不是以最大价值赢时,您对策略的想法。像上面的问题一样,硬币的数量是偶数。 贪婪的方法能很好地工作并给出最优的解决方案吗?如果硬币的数量是奇数,你的答案会改变吗?请看 两个角落的硬币游戏 本文由 阿希什·巴恩瓦尔 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



