编写一个函数来检测两棵树是否同构。两棵树被称为同构树,如果其中一棵树可以通过一系列翻转从另一棵树获得,即通过交换多个节点的左右子树。任何级别的任意数量的节点都可以交换其子节点。两棵空树是同构的。 例如,以下两棵树同构,以下子树翻转:2和3,NULL和6,7和8。
null
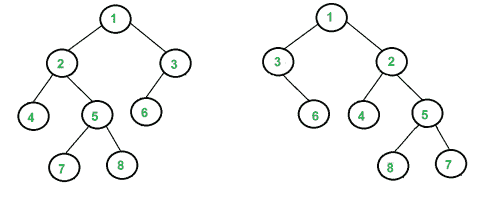
我们同时穿过两棵树。让正在遍历的两棵树的当前内部节点 n1 和 n2 分别地以n1和n2为根的子树同构有以下两个条件。 1) n1和n2的数据相同。 2) 以下两种情况之一适用于n1和n2的儿童 …… (a) n1的左子代同构于n2的左子代,n1的右子代同构于n2的右子代。 …… b) n1的左子代同构于n2的右子代,n1的右子代同构于n2的左子代。
C++
// A C++ program to check if two given trees are isomorphic #include <iostream> using namespace std; /* A binary tree node has data, pointer to left and right children */ struct node { int data; struct node* left; struct node* right; }; /* Given a binary tree, print its nodes in reverse level order */ bool isIsomorphic(node* n1, node *n2) { // Both roots are NULL, trees isomorphic by definition if (n1 == NULL && n2 == NULL) return true ; // Exactly one of the n1 and n2 is NULL, trees not isomorphic if (n1 == NULL || n2 == NULL) return false ; if (n1->data != n2->data) return false ; // There are two possible cases for n1 and n2 to be isomorphic // Case 1: The subtrees rooted at these nodes have NOT been "Flipped". // Both of these subtrees have to be isomorphic, hence the && // Case 2: The subtrees rooted at these nodes have been "Flipped" return (isIsomorphic(n1->left,n2->left) && isIsomorphic(n1->right,n2->right))|| (isIsomorphic(n1->left,n2->right) && isIsomorphic(n1->right,n2->left)); } /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ node* newNode( int data) { node* temp = new node; temp->data = data; temp->left = NULL; temp->right = NULL; return (temp); } /* Driver program to test above functions*/ int main() { // Let us create trees shown in above diagram struct node *n1 = newNode(1); n1->left = newNode(2); n1->right = newNode(3); n1->left->left = newNode(4); n1->left->right = newNode(5); n1->right->left = newNode(6); n1->left->right->left = newNode(7); n1->left->right->right = newNode(8); struct node *n2 = newNode(1); n2->left = newNode(3); n2->right = newNode(2); n2->right->left = newNode(4); n2->right->right = newNode(5); n2->left->right = newNode(6); n2->right->right->left = newNode(8); n2->right->right->right = newNode(7); if (isIsomorphic(n1, n2) == true ) cout << "Yes" ; else cout << "No" ; return 0; } |
JAVA
// An iterative java program to solve tree isomorphism problem /* A binary tree node has data, pointer to left and right children */ class Node { int data; Node left, right; Node( int item) { data = item; left = right; } } class BinaryTree { Node root1, root2; /* Given a binary tree, print its nodes in reverse level order */ boolean isIsomorphic(Node n1, Node n2) { // Both roots are NULL, trees isomorphic by definition if (n1 == null && n2 == null ) return true ; // Exactly one of the n1 and n2 is NULL, trees not isomorphic if (n1 == null || n2 == null ) return false ; if (n1.data != n2.data) return false ; // There are two possible cases for n1 and n2 to be isomorphic // Case 1: The subtrees rooted at these nodes have NOT been // "Flipped". // Both of these subtrees have to be isomorphic. // Case 2: The subtrees rooted at these nodes have been "Flipped" return (isIsomorphic(n1.left, n2.left) && isIsomorphic(n1.right, n2.right)) || (isIsomorphic(n1.left, n2.right) && isIsomorphic(n1.right, n2.left)); } // Driver program to test above functions public static void main(String args[]) { BinaryTree tree = new BinaryTree(); // Let us create trees shown in above diagram tree.root1 = new Node( 1 ); tree.root1.left = new Node( 2 ); tree.root1.right = new Node( 3 ); tree.root1.left.left = new Node( 4 ); tree.root1.left.right = new Node( 5 ); tree.root1.right.left = new Node( 6 ); tree.root1.left.right.left = new Node( 7 ); tree.root1.left.right.right = new Node( 8 ); tree.root2 = new Node( 1 ); tree.root2.left = new Node( 3 ); tree.root2.right = new Node( 2 ); tree.root2.right.left = new Node( 4 ); tree.root2.right.right = new Node( 5 ); tree.root2.left.right = new Node( 6 ); tree.root2.right.right.left = new Node( 8 ); tree.root2.right.right.right = new Node( 7 ); if (tree.isIsomorphic(tree.root1, tree.root2) == true ) System.out.println( "Yes" ); else System.out.println( "No" ); } } // This code has been contributed by Mayank Jaiswal |
Python3
# Python program to check if two given trees are isomorphic # A Binary tree node class Node: # Constructor to create the node of binary tree def __init__( self , data): self .data = data self .left = None self .right = None # Check if the binary tree is isomorphic or not def isIsomorphic(n1, n2): # Both roots are None, trees isomorphic by definition if n1 is None and n2 is None : return True # Exactly one of the n1 and n2 is None, trees are not # isomorphic if n1 is None or n2 is None : return False if n1.data ! = n2.data : return False # There are two possible cases for n1 and n2 to be isomorphic # Case 1: The subtrees rooted at these nodes have NOT # been "Flipped". # Both of these subtrees have to be isomorphic, hence the && # Case 2: The subtrees rooted at these nodes have # been "Flipped" return ((isIsomorphic(n1.left, n2.left) and isIsomorphic(n1.right, n2.right)) or (isIsomorphic(n1.left, n2.right) and isIsomorphic(n1.right, n2.left)) ) # Driver program to test above function n1 = Node( 1 ) n1.left = Node( 2 ) n1.right = Node( 3 ) n1.left.left = Node( 4 ) n1.left.right = Node( 5 ) n1.right.left = Node( 6 ) n1.left.right.left = Node( 7 ) n1.left.right.right = Node( 8 ) n2 = Node( 1 ) n2.left = Node( 3 ) n2.right = Node( 2 ) n2.right.left = Node( 4 ) n2.right.right = Node( 5 ) n2.left.right = Node( 6 ) n2.right.right.left = Node( 8 ) n2.right.right.right = Node( 7 ) print ( "Yes" if (isIsomorphic(n1, n2) = = True ) else "No" ) # This code is contributed by Nikhil Kumar Singh(nickzuck_007) |
C#
using System; // An iterative C# program to solve tree isomorphism problem /* A binary tree node has data, pointer to left and right children */ public class Node { public int data; public Node left, right; public Node( int item) { data = item; left = right; } } public class BinaryTree { public Node root1, root2; /* Given a binary tree, print its nodes in reverse level order */ public virtual bool isIsomorphic(Node n1, Node n2) { // Both roots are NULL, trees isomorphic by definition if (n1 == null && n2 == null ) { return true ; } // Exactly one of the n1 and n2 is NULL, trees not isomorphic if (n1 == null || n2 == null ) { return false ; } if (n1.data != n2.data) { return false ; } // There are two possible cases for n1 and n2 to be isomorphic // Case 1: The subtrees rooted at these nodes have NOT been // "Flipped". // Both of these subtrees have to be isomorphic. // Case 2: The subtrees rooted at these nodes have been "Flipped" return (isIsomorphic(n1.left, n2.left) && isIsomorphic(n1.right, n2.right)) || (isIsomorphic(n1.left, n2.right) && isIsomorphic(n1.right, n2.left)); } // Driver program to test above functions public static void Main( string [] args) { BinaryTree tree = new BinaryTree(); // Let us create trees shown in above diagram tree.root1 = new Node(1); tree.root1.left = new Node(2); tree.root1.right = new Node(3); tree.root1.left.left = new Node(4); tree.root1.left.right = new Node(5); tree.root1.right.left = new Node(6); tree.root1.left.right.left = new Node(7); tree.root1.left.right.right = new Node(8); tree.root2 = new Node(1); tree.root2.left = new Node(3); tree.root2.right = new Node(2); tree.root2.right.left = new Node(4); tree.root2.right.right = new Node(5); tree.root2.left.right = new Node(6); tree.root2.right.right.left = new Node(8); tree.root2.right.right.right = new Node(7); if (tree.isIsomorphic(tree.root1, tree.root2) == true ) { Console.WriteLine( "Yes" ); } else { Console.WriteLine( "No" ); } } } // This code is contributed by Shrikant13 |
Javascript
<script> // An iterative JavaScript program // to solve tree isomorphism problem /* A binary tree node has data, pointer to left and right children */ class Node { constructor(item) { this .data = item; this .left = null ; this .right = null ; } } class BinaryTree { constructor() { this .root1 = null ; this .root2 = null ; } /* Given a binary tree, print its nodes in reverse level order */ isIsomorphic(n1, n2) { // Both roots are NULL, trees isomorphic by definition if (n1 == null && n2 == null ) { return true ; } // Exactly one of the n1 and n2 is NULL, // trees not isomorphic if (n1 == null || n2 == null ) { return false ; } if (n1.data != n2.data) { return false ; } // There are two possible cases for // n1 and n2 to be isomorphic // Case 1: The subtrees rooted at // these nodes have NOT been // "Flipped". // Both of these subtrees have to be isomorphic. // Case 2: The subtrees rooted at these nodes // have been "Flipped" return ( ( this .isIsomorphic(n1.left, n2.left) && this .isIsomorphic(n1.right, n2.right)) || ( this .isIsomorphic(n1.left, n2.right) && this .isIsomorphic(n1.right, n2.left)) ); } } // Driver program to test above functions var tree = new BinaryTree(); // Let us create trees shown in above diagram tree.root1 = new Node(1); tree.root1.left = new Node(2); tree.root1.right = new Node(3); tree.root1.left.left = new Node(4); tree.root1.left.right = new Node(5); tree.root1.right.left = new Node(6); tree.root1.left.right.left = new Node(7); tree.root1.left.right.right = new Node(8); tree.root2 = new Node(1); tree.root2.left = new Node(3); tree.root2.right = new Node(2); tree.root2.right.left = new Node(4); tree.root2.right.right = new Node(5); tree.root2.left.right = new Node(6); tree.root2.right.right.left = new Node(8); tree.root2.right.right.right = new Node(7); if (tree.isIsomorphic(tree.root1, tree.root2) == true ) { document.write( "Yes" ); } else { document.write( "No" ); } </script> |
输出:
Yes
时间复杂性: 上述解决方案遍历两棵树。所以时间复杂度是O(min(m,n)*2)或O(min(m,n)),其中m和n是给定树中的节点数。
本文由 西弗 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论。 如果你喜欢GeekSforgeks,并且想贡献自己的力量,你也可以写一篇文章,然后把你的文章邮寄给评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



