给定一个无向图和一个数字m,确定该图是否最多可以用m种颜色着色,以确保该图的两个相邻顶点没有用相同的颜色着色。这里,图的着色意味着将颜色分配给所有顶点。
输入输出格式:
输入:
- 二维数组图[V][V]其中V是图中的顶点数,图[V][V]是图的邻接矩阵表示。如果从i到j有一条直边,则值图[i][j]为1,否则图[i][j]为0。
- 整数m是可以使用的最大颜色数。
输出: 数组颜色[V]的数字应为1到m。颜色[i]应表示分配给第i个顶点的颜色。如果图形不能用m颜色着色,代码也应该返回false。
例子:
Input: graph = {0, 1, 1, 1}, {1, 0, 1, 0}, {1, 1, 0, 1}, {1, 0, 1, 0}Output: Solution Exists: Following are the assigned colors 1 2 3 2Explanation: By coloring the vertices with following colors, adjacent vertices does not have same colorsInput: graph = {1, 1, 1, 1}, {1, 1, 1, 1}, {1, 1, 1, 1}, {1, 1, 1, 1}Output: Solution does not exist.Explanation: No solution exits.
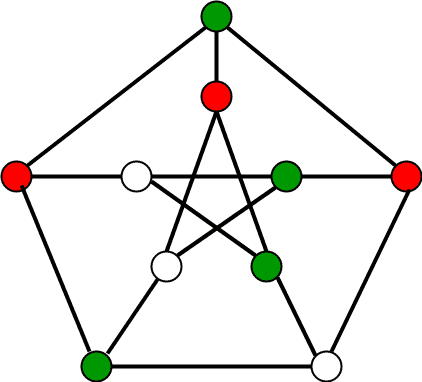
下面是一个可以用3种不同颜色着色的图形示例。
我们强烈建议您在继续解决方案之前单击此处并进行练习。
方法1: 缺乏经验的
天真的方法: 生成所有可能的颜色配置。由于每个节点都可以使用m种可用颜色中的任意一种进行着色,因此可能的颜色配置总数为m^V。 生成颜色配置后,检查相邻顶点是否具有相同的颜色。如果满足条件,打印组合并断开循环。
算法:
- 创建一个递归函数,用于获取当前索引、顶点数和输出颜色数组。
- 如果当前索引等于顶点数。检查输出颜色配置是否安全,即检查相邻顶点是否具有相同的颜色。如果满足条件,打印配置并断开。
- 为顶点指定颜色(1到m)。
- 对于每个指定的颜色,递归调用具有下一个索引和顶点数的函数
- 如果任何递归函数返回true,则中断循环并返回true。
以下是上述理念的实施情况:
C++
#include<bits/stdc++.h> using namespace std; // Number of vertices in the graph #define V 4 void printSolution( int color[]); // check if the colored // graph is safe or not bool isSafe( bool graph[V][V], int color[]) { // check for every edge for ( int i = 0; i < V; i++) for ( int j = i + 1; j < V; j++) if (graph[i][j] && color[j] == color[i]) return false ; return true ; } /* This function solves the m Coloring problem using recursion. It returns false if the m colours cannot be assigned, otherwise, return true and prints assignments of colours to all vertices. Please note that there may be more than one solutions, this function prints one of the feasible solutions.*/ bool graphColoring( bool graph[V][V], int m, int i, int color[V]) { // if current index reached end if (i == V) { // if coloring is safe if (isSafe(graph, color)) { // Print the solution printSolution(color); return true ; } return false ; } // Assign each color from 1 to m for ( int j = 1; j <= m; j++) { color[i] = j; // Recur of the rest vertices if (graphColoring(graph, m, i + 1, color)) return true ; color[i] = 0; } return false ; } /* A utility function to print solution */ void printSolution( int color[]) { cout << "Solution Exists:" " Following are the assigned colors " ; for ( int i = 0; i < V; i++) cout << " " << color[i]; cout << "" ; } // Driver code int main() { /* Create following graph and test whether it is 3 colorable (3)---(2) | / | | / | | / | (0)---(1) */ bool graph[V][V] = { { 0, 1, 1, 1 }, { 1, 0, 1, 0 }, { 1, 1, 0, 1 }, { 1, 0, 1, 0 }, }; int m = 3; // Number of colors // Initialize all color values as 0. // This initialization is needed // correct functioning of isSafe() int color[V]; for ( int i = 0; i < V; i++) color[i] = 0; if (!graphColoring(graph, m, 0, color)) cout << "Solution does not exist" ; return 0; } // This code is contributed by shivanisinghss2110 |
C
#include <stdbool.h> #include <stdio.h> // Number of vertices in the graph #define V 4 void printSolution( int color[]); // check if the colored // graph is safe or not bool isSafe( bool graph[V][V], int color[]) { // check for every edge for ( int i = 0; i < V; i++) for ( int j = i + 1; j < V; j++) if (graph[i][j] && color[j] == color[i]) return false ; return true ; } /* This function solves the m Coloring problem using recursion. It returns false if the m colours cannot be assigned, otherwise, return true and prints assignments of colours to all vertices. Please note that there may be more than one solutions, this function prints one of the feasible solutions.*/ bool graphColoring( bool graph[V][V], int m, int i, int color[V]) { // if current index reached end if (i == V) { // if coloring is safe if (isSafe(graph, color)) { // Print the solution printSolution(color); return true ; } return false ; } // Assign each color from 1 to m for ( int j = 1; j <= m; j++) { color[i] = j; // Recur of the rest vertices if (graphColoring(graph, m, i + 1, color)) return true ; color[i] = 0; } return false ; } /* A utility function to print solution */ void printSolution( int color[]) { printf ( "Solution Exists:" " Following are the assigned colors " ); for ( int i = 0; i < V; i++) printf ( " %d " , color[i]); printf ( "" ); } // Driver program to test above function int main() { /* Create following graph and test whether it is 3 colorable (3)---(2) | / | | / | | / | (0)---(1) */ bool graph[V][V] = { { 0, 1, 1, 1 }, { 1, 0, 1, 0 }, { 1, 1, 0, 1 }, { 1, 0, 1, 0 }, }; int m = 3; // Number of colors // Initialize all color values as 0. // This initialization is needed // correct functioning of isSafe() int color[V]; for ( int i = 0; i < V; i++) color[i] = 0; if (!graphColoring(graph, m, 0, color)) printf ( "Solution does not exist" ); return 0; } |
JAVA
public class GFG { // Number of vertices in the graph static int V = 4 ; /* A utility function to print solution */ static void printSolution( int [] color) { System.out.println( "Solution Exists:" + " Following are the assigned colors " ); for ( int i = 0 ; i < V; i++) System.out.print( " " + color[i]); System.out.println(); } // check if the colored // graph is safe or not static boolean isSafe( boolean [][] graph, int [] color) { // check for every edge for ( int i = 0 ; i < V; i++) for ( int j = i + 1 ; j < V; j++) if (graph[i][j] && color[j] == color[i]) return false ; return true ; } /* This function solves the m Coloring problem using recursion. It returns false if the m colours cannot be assigned, otherwise, return true and prints assignments of colours to all vertices. Please note that there may be more than one solutions, this function prints one of the feasible solutions.*/ static boolean graphColoring( boolean [][] graph, int m, int i, int [] color) { // if current index reached end if (i == V) { // if coloring is safe if (isSafe(graph, color)) { // Print the solution printSolution(color); return true ; } return false ; } // Assign each color from 1 to m for ( int j = 1 ; j <= m; j++) { color[i] = j; // Recur of the rest vertices if (graphColoring(graph, m, i + 1 , color)) return true ; color[i] = 0 ; } return false ; } // Driver code public static void main(String[] args) { /* Create following graph and test whether it is 3 colorable (3)---(2) | / | | / | | / | (0)---(1) */ boolean [][] graph = { { false , true , true , true }, { true , false , true , false }, { true , true , false , true }, { true , false , true , false }, }; int m = 3 ; // Number of colors // Initialize all color values as 0. // This initialization is needed // correct functioning of isSafe() int [] color = new int [V]; for ( int i = 0 ; i < V; i++) color[i] = 0 ; if (!graphColoring(graph, m, 0 , color)) System.out.println( "Solution does not exist" ); } } // This code is contributed by divyeh072019. |
Python3
# Number of vertices in the graph # define 4 4 # check if the colored # graph is safe or not def isSafe(graph, color): # check for every edge for i in range ( 4 ): for j in range (i + 1 , 4 ): if (graph[i][j] and color[j] = = color[i]): return False return True # /* This function solves the m Coloring # problem using recursion. It returns # false if the m colours cannot be assigned, # otherwise, return true and prints # assignments of colours to all vertices. # Please note that there may be more than # one solutions, this function prints one # of the feasible solutions.*/ def graphColoring(graph, m, i, color): # if current index reached end if (i = = 4 ): # if coloring is safe if (isSafe(graph, color)): # Print the solution printSolution(color) return True return False # Assign each color from 1 to m for j in range ( 1 , m + 1 ): color[i] = j # Recur of the rest vertices if (graphColoring(graph, m, i + 1 , color)): return True color[i] = 0 return False # /* A utility function to print solution */ def printSolution(color): print ( "Solution Exists:" " Following are the assigned colors " ) for i in range ( 4 ): print (color[i],end = " " ) # Driver code if __name__ = = '__main__' : # /* Create following graph and # test whether it is 3 colorable # (3)---(2) # | / | # | / | # | / | # (0)---(1) # */ graph = [ [ 0 , 1 , 1 , 1 ], [ 1 , 0 , 1 , 0 ], [ 1 , 1 , 0 , 1 ], [ 1 , 0 , 1 , 0 ], ] m = 3 # Number of colors # Initialize all color values as 0. # This initialization is needed # correct functioning of isSafe() color = [ 0 for i in range ( 4 )] if ( not graphColoring(graph, m, 0 , color)): print ( "Solution does not exist" ) # This code is contributed by mohit kumar 29 |
C#
using System; class GFG { // Number of vertices in the graph static int V = 4; /* A utility function to print solution */ static void printSolution( int [] color) { Console.WriteLine( "Solution Exists:" + " Following are the assigned colors " ); for ( int i = 0; i < V; i++) Console.Write( " " + color[i]); Console.WriteLine(); } // check if the colored // graph is safe or not static bool isSafe( bool [,] graph, int [] color) { // check for every edge for ( int i = 0; i < V; i++) for ( int j = i + 1; j < V; j++) if (graph[i, j] && color[j] == color[i]) return false ; return true ; } /* This function solves the m Coloring problem using recursion. It returns false if the m colours cannot be assigned, otherwise, return true and prints assignments of colours to all vertices. Please note that there may be more than one solutions, this function prints one of the feasible solutions.*/ static bool graphColoring( bool [,] graph, int m, int i, int [] color) { // if current index reached end if (i == V) { // if coloring is safe if (isSafe(graph, color)) { // Print the solution printSolution(color); return true ; } return false ; } // Assign each color from 1 to m for ( int j = 1; j <= m; j++) { color[i] = j; // Recur of the rest vertices if (graphColoring(graph, m, i + 1, color)) return true ; color[i] = 0; } return false ; } // Driver code static void Main() { /* Create following graph and test whether it is 3 colorable (3)---(2) | / | | / | | / | (0)---(1) */ bool [,] graph = { { false , true , true , true }, { true , false , true , false }, { true , true , false , true }, { true , false , true , false }, }; int m = 3; // Number of colors // Initialize all color values as 0. // This initialization is needed // correct functioning of isSafe() int [] color = new int [V]; for ( int i = 0; i < V; i++) color[i] = 0; if (!graphColoring(graph, m, 0, color)) Console.WriteLine( "Solution does not exist" ); } } // this code is contributed by divyeshrabadiya07. |
Javascript
<script> // Number of vertices in the graph let V = 4; /* A utility function to print solution */ function printSolution(color) { document.write( "Solution Exists:" + " Following are the assigned colors <br>" ); for (let i = 0; i < V; i++) document.write( " " + color[i]); document.write( " " ); } // check if the colored // graph is safe or not function isSafe(graph,color) { // check for every edge for (let i = 0; i < V; i++) for (let j = i + 1; j < V; j++) if (graph[i][j] && color[j] == color[i]) return false ; return true ; } /* This function solves the m Coloring problem using recursion. It returns false if the m colours cannot be assigned, otherwise, return true and prints assignments of colours to all vertices. Please note that there may be more than one solutions, this function prints one of the feasible solutions.*/ function graphColoring(graph,m,i,color) { // if current index reached end if (i == V) { // if coloring is safe if (isSafe(graph, color)) { // Print the solution printSolution(color); return true ; } return false ; } // Assign each color from 1 to m for (let j = 1; j <= m; j++) { color[i] = j; // Recur of the rest vertices if (graphColoring(graph, m, i + 1, color)) return true ; color[i] = 0; } return false ; } // Driver code /* Create following graph and test whether it is 3 colorable (3)---(2) | / | | / | | / | (0)---(1) */ let graph=[[ false , true , true , true ], [ true , false , true , false ], [ true , true , false , true ], [ true , false , true , false ]]; let m = 3; // Number of colors // Initialize all color values as 0. // This initialization is needed // correct functioning of isSafe() let color = new Array(V); for (let i = 0; i < V; i++) color[i] = 0; if (!graphColoring(graph, m, 0, color)) document.write( "Solution does not exist" ); // This code is contributed by unknown2108 </script> |
Solution Exists: Following are the assigned colors 1 2 3 2
复杂性分析:
- 时间复杂性: O(m^V)。 有一个完全O(m^V)的颜色组合。所以时间复杂度是O(m^V)。
- 空间复杂性: O(V)。 GraphColor(…)函数的递归堆栈将需要O(V)空间。
方法2 : 回溯 .
方法: 其思想是从顶点0开始,逐个为不同的顶点指定颜色。在指定颜色之前,通过考虑已为相邻顶点指定的颜色来检查安全性,即检查相邻顶点是否具有相同的颜色。如果存在任何不违反条件的颜色指定,请将颜色指定标记为解决方案的一部分。如果无法指定颜色,则回溯并返回false。
算法:
- 创建一个递归函数,用于获取图形、当前索引、顶点数和输出颜色数组。
- 如果当前索引等于顶点数。在输出阵列中打印颜色配置。
- 为顶点指定颜色(1到m)。
- 对于每个指定的颜色,检查配置是否安全(即检查相邻顶点是否不具有相同的颜色),使用下一个索引和顶点数递归调用函数
- 如果任何递归函数返回true,则中断循环并返回true。
- 如果没有递归函数返回true,则返回false。
以下是上述理念的实施情况:
C++
// C++ program for solution of M // Coloring problem using backtracking #include <iostream> using namespace std; // Number of vertices in the graph #define V 4 void printSolution( int color[]); /* A utility function to check if the current color assignment is safe for vertex v i.e. checks whether the edge exists or not (i.e, graph[v][i]==1). If exist then checks whether the color to be filled in the new vertex(c is sent in the parameter) is already used by its adjacent vertices(i-->adj vertices) or not (i.e, color[i]==c) */ bool isSafe( int v, bool graph[V][V], int color[], int c) { for ( int i = 0; i < V; i++) if (graph[v][i] && c == color[i]) return false ; return true ; } /* A recursive utility function to solve m coloring problem */ bool graphColoringUtil( bool graph[V][V], int m, int color[], int v) { /* base case: If all vertices are assigned a color then return true */ if (v == V) return true ; /* Consider this vertex v and try different colors */ for ( int c = 1; c <= m; c++) { /* Check if assignment of color c to v is fine*/ if (isSafe(v, graph, color, c)) { color[v] = c; /* recur to assign colors to rest of the vertices */ if (graphColoringUtil( graph, m, color, v + 1) == true ) return true ; /* If assigning color c doesn't lead to a solution then remove it */ color[v] = 0; } } /* If no color can be assigned to this vertex then return false */ return false ; } /* This function solves the m Coloring problem using Backtracking. It mainly uses graphColoringUtil() to solve the problem. It returns false if the m colors cannot be assigned, otherwise return true and prints assignments of colors to all vertices. Please note that there may be more than one solutions, this function prints one of the feasible solutions.*/ bool graphColoring( bool graph[V][V], int m) { // Initialize all color values as 0. // This initialization is needed // correct functioning of isSafe() int color[V]; for ( int i = 0; i < V; i++) color[i] = 0; // Call graphColoringUtil() for vertex 0 if (graphColoringUtil(graph, m, color, 0) == false ) { cout << "Solution does not exist" ; return false ; } // Print the solution printSolution(color); return true ; } /* A utility function to print solution */ void printSolution( int color[]) { cout << "Solution Exists:" << " Following are the assigned colors" << "" ; for ( int i = 0; i < V; i++) cout << " " << color[i] << " " ; cout << "" ; } // Driver code int main() { /* Create following graph and test whether it is 3 colorable (3)---(2) | / | | / | | / | (0)---(1) */ bool graph[V][V] = { { 0, 1, 1, 1 }, { 1, 0, 1, 0 }, { 1, 1, 0, 1 }, { 1, 0, 1, 0 }, }; // Number of colors int m = 3; graphColoring(graph, m); return 0; } // This code is contributed by Shivani |
C
#include <stdbool.h> #include <stdio.h> // Number of vertices in the graph #define V 4 void printSolution( int color[]); /* A utility function to check if the current color assignment is safe for vertex v i.e. checks whether the edge exists or not (i.e, graph[v][i]==1). If exist then checks whether the color to be filled in the new vertex(c is sent in the parameter) is already used by its adjacent vertices(i-->adj vertices) or not (i.e, color[i]==c) */ bool isSafe( int v, bool graph[V][V], int color[], int c) { for ( int i = 0; i < V; i++) if ( graph[v][i] && c == color[i]) return false ; return true ; } /* A recursive utility function to solve m coloring problem */ bool graphColoringUtil( bool graph[V][V], int m, int color[], int v) { /* base case: If all vertices are assigned a color then return true */ if (v == V) return true ; /* Consider this vertex v and try different colors */ for ( int c = 1; c <= m; c++) { /* Check if assignment of color c to v is fine*/ if (isSafe( v, graph, color, c)) { color[v] = c; /* recur to assign colors to rest of the vertices */ if ( graphColoringUtil( graph, m, color, v + 1) == true ) return true ; /* If assigning color c doesn't lead to a solution then remove it */ color[v] = 0; } } /* If no color can be assigned to this vertex then return false */ return false ; } /* This function solves the m Coloring problem using Backtracking. It mainly uses graphColoringUtil() to solve the problem. It returns false if the m colors cannot be assigned, otherwise return true and prints assignments of colors to all vertices. Please note that there may be more than one solutions, this function prints one of the feasible solutions.*/ bool graphColoring( bool graph[V][V], int m) { // Initialize all color values as 0. // This initialization is needed // correct functioning of isSafe() int color[V]; for ( int i = 0; i < V; i++) color[i] = 0; // Call graphColoringUtil() for vertex 0 if ( graphColoringUtil( graph, m, color, 0) == false ) { printf ( "Solution does not exist" ); return false ; } // Print the solution printSolution(color); return true ; } /* A utility function to print solution */ void printSolution( int color[]) { printf ( "Solution Exists:" " Following are the assigned colors " ); for ( int i = 0; i < V; i++) printf ( " %d " , color[i]); printf ( "" ); } // driver program to test above function int main() { /* Create following graph and test whether it is 3 colorable (3)---(2) | / | | / | | / | (0)---(1) */ bool graph[V][V] = { { 0, 1, 1, 1 }, { 1, 0, 1, 0 }, { 1, 1, 0, 1 }, { 1, 0, 1, 0 }, }; int m = 3; // Number of colors graphColoring(graph, m); return 0; } |
JAVA
/* Java program for solution of M Coloring problem using backtracking */ public class mColoringProblem { final int V = 4 ; int color[]; /* A utility function to check if the current color assignment is safe for vertex v */ boolean isSafe( int v, int graph[][], int color[], int c) { for ( int i = 0 ; i < V; i++) if ( graph[v][i] == 1 && c == color[i]) return false ; return true ; } /* A recursive utility function to solve m coloring problem */ boolean graphColoringUtil( int graph[][], int m, int color[], int v) { /* base case: If all vertices are assigned a color then return true */ if (v == V) return true ; /* Consider this vertex v and try different colors */ for ( int c = 1 ; c <= m; c++) { /* Check if assignment of color c to v is fine*/ if (isSafe(v, graph, color, c)) { color[v] = c; /* recur to assign colors to rest of the vertices */ if ( graphColoringUtil( graph, m, color, v + 1 )) return true ; /* If assigning color c doesn't lead to a solution then remove it */ color[v] = 0 ; } } /* If no color can be assigned to this vertex then return false */ return false ; } /* This function solves the m Coloring problem using Backtracking. It mainly uses graphColoringUtil() to solve the problem. It returns false if the m colors cannot be assigned, otherwise return true and prints assignments of colors to all vertices. Please note that there may be more than one solutions, this function prints one of the feasible solutions.*/ boolean graphColoring( int graph[][], int m) { // Initialize all color values as 0. This // initialization is needed correct // functioning of isSafe() color = new int [V]; for ( int i = 0 ; i < V; i++) color[i] = 0 ; // Call graphColoringUtil() for vertex 0 if ( !graphColoringUtil( graph, m, color, 0 )) { System.out.println( "Solution does not exist" ); return false ; } // Print the solution printSolution(color); return true ; } /* A utility function to print solution */ void printSolution( int color[]) { System.out.println( "Solution Exists: Following" + " are the assigned colors" ); for ( int i = 0 ; i < V; i++) System.out.print( " " + color[i] + " " ); System.out.println(); } // driver program to test above function public static void main(String args[]) { mColoringProblem Coloring = new mColoringProblem(); /* Create following graph and test whether it is 3 colorable (3)---(2) | / | | / | | / | (0)---(1) */ int graph[][] = { { 0 , 1 , 1 , 1 }, { 1 , 0 , 1 , 0 }, { 1 , 1 , 0 , 1 }, { 1 , 0 , 1 , 0 }, }; int m = 3 ; // Number of colors Coloring.graphColoring(graph, m); } } // This code is contributed by Abhishek Shankhadhar |
Python3
# Python program for solution of M Coloring # problem using backtracking class Graph(): def __init__( self , vertices): self .V = vertices self .graph = [[ 0 for column in range (vertices)] for row in range (vertices)] # A utility function to check # if the current color assignment # is safe for vertex v def isSafe( self , v, colour, c): for i in range ( self .V): if self .graph[v][i] = = 1 and colour[i] = = c: return False return True # A recursive utility function to solve m # coloring problem def graphColourUtil( self , m, colour, v): if v = = self .V: return True for c in range ( 1 , m + 1 ): if self .isSafe(v, colour, c) = = True : colour[v] = c if self .graphColourUtil(m, colour, v + 1 ) = = True : return True colour[v] = 0 def graphColouring( self , m): colour = [ 0 ] * self .V if self .graphColourUtil(m, colour, 0 ) = = None : return False # Print the solution print ( "Solution exist and Following are the assigned colours:" ) for c in colour: print (c,end = ' ' ) return True # Driver Code g = Graph( 4 ) g.graph = [[ 0 , 1 , 1 , 1 ], [ 1 , 0 , 1 , 0 ], [ 1 , 1 , 0 , 1 ], [ 1 , 0 , 1 , 0 ]] m = 3 g.graphColouring(m) # This code is contributed by Divyanshu Mehta |
C#
/* C# program for solution of M Coloring problem using backtracking */ using System; class GFG { readonly int V = 4; int [] color; /* A utility function to check if the current color assignment is safe for vertex v */ bool isSafe( int v, int [, ] graph, int [] color, int c) { for ( int i = 0; i < V; i++) if (graph[v, i] == 1 && c == color[i]) return false ; return true ; } /* A recursive utility function to solve m coloring problem */ bool graphColoringUtil( int [, ] graph, int m, int [] color, int v) { /* base case: If all vertices are assigned a color then return true */ if (v == V) return true ; /* Consider this vertex v and try different colors */ for ( int c = 1; c <= m; c++) { /* Check if assignment of color c to v is fine*/ if (isSafe(v, graph, color, c)) { color[v] = c; /* recur to assign colors to rest of the vertices */ if (graphColoringUtil(graph, m, color, v + 1)) return true ; /* If assigning color c doesn't lead to a solution then remove it */ color[v] = 0; } } /* If no color can be assigned to this vertex then return false */ return false ; } /* This function solves the m Coloring problem using Backtracking. It mainly uses graphColoringUtil() to solve the problem. It returns false if the m colors cannot be assigned, otherwise return true and prints assignments of colors to all vertices. Please note that there may be more than one solutions, this function prints one of the feasible solutions.*/ bool graphColoring( int [, ] graph, int m) { // Initialize all color values as 0. This // initialization is needed correct functioning // of isSafe() color = new int [V]; for ( int i = 0; i < V; i++) color[i] = 0; // Call graphColoringUtil() for vertex 0 if (!graphColoringUtil(graph, m, color, 0)) { Console.WriteLine( "Solution does not exist" ); return false ; } // Print the solution printSolution(color); return true ; } /* A utility function to print solution */ void printSolution( int [] color) { Console.WriteLine( "Solution Exists: Following" + " are the assigned colors" ); for ( int i = 0; i < V; i++) Console.Write( " " + color[i] + " " ); Console.WriteLine(); } // Driver Code public static void Main(String[] args) { GFG Coloring = new GFG(); /* Create following graph and test whether it is 3 colorable (3)---(2) | / | | / | | / | (0)---(1) */ int [, ] graph = { { 0, 1, 1, 1 }, { 1, 0, 1, 0 }, { 1, 1, 0, 1 }, { 1, 0, 1, 0 } }; int m = 3; // Number of colors Coloring.graphColoring(graph, m); } } // This code is contributed by PrinciRaj1992 |
Javascript
<script> /* JavaScript program for solution of M Coloring problem using backtracking */ let V = 4; let color; /* A utility function to check if the current color assignment is safe for vertex v */ function isSafe(v,graph,color,c) { for (let i = 0; i < V; i++) if ( graph[v][i] == 1 && c == color[i]) return false ; return true ; } /* A recursive utility function to solve m coloring problem */ function graphColoringUtil(graph,m,color,v) { /* base case: If all vertices are assigned a color then return true */ if (v == V) return true ; /* Consider this vertex v and try different colors */ for (let c = 1; c <= m; c++) { /* Check if assignment of color c to v is fine*/ if (isSafe(v, graph, color, c)) { color[v] = c; /* recur to assign colors to rest of the vertices */ if ( graphColoringUtil( graph, m, color, v + 1)) return true ; /* If assigning color c doesn't lead to a solution then remove it */ color[v] = 0; } } /* If no color can be assigned to this vertex then return false */ return false ; } /* This function solves the m Coloring problem using Backtracking. It mainly uses graphColoringUtil() to solve the problem. It returns false if the m colors cannot be assigned, otherwise return true and prints assignments of colors to all vertices. Please note that there may be more than one solutions, this function prints one of the feasible solutions.*/ function graphColoring(graph,m) { // Initialize all color values as 0. This // initialization is needed correct // functioning of isSafe() color = new Array(V); for (let i = 0; i < V; i++) color[i] = 0; // Call graphColoringUtil() for vertex 0 if ( !graphColoringUtil( graph, m, color, 0)) { document.write( "Solution does not exist<br>" ); return false ; } // Print the solution printSolution(color); return true ; } /* A utility function to print solution */ function printSolution(color) { document.write( "Solution Exists: Following" + " are the assigned colors<br>" ); for (let i = 0; i < V; i++) document.write( " " + color[i] + " " ); document.write( "<br>" ); } // driver program to test above function /* Create following graph and test whether it is 3 colorable (3)---(2) | / | | / | | / | (0)---(1) */ let graph = [ [ 0, 1, 1, 1 ], [ 1, 0, 1, 0 ], [ 1, 1, 0, 1 ], [ 1, 0, 1, 0 ], ]; let m = 3; // Number of colors graphColoring(graph, m); // This code is contributed by ab2127 </script> |
Solution Exists: Following are the assigned colors 1 2 3 2
复杂性分析:
- 时间复杂性: O(m^V)。 有总O(m^V)的颜色组合。所以时间复杂度是O(m^V)。上限时间复杂度保持不变,但所用的平均时间将更少。
- 空间复杂性: O(V)。 GraphColor(…)函数的递归堆栈将需要O(V)空间。
方法3: 使用BFS
这里的方法是先用颜色1将每个节点从1着色到n。并从未访问的起始节点开始移动BFS,以一次性覆盖所有连接的组件。在BFS遍历过程中到达每个节点时,请执行以下操作:
- 检查给定节点的所有边。
- 对于通过边连接到节点的每个顶点:
- 检查节点的颜色是否相同。如果相同,则将另一个节点(不是当前节点)的颜色增加一。
- 检查它是否被访问过。如果未访问,则将其标记为已访问,并将其推到队列中。
- 到目前为止,请检查MaxColor的条件。如果超过M,则返回false
访问所有节点后,返回true(因为在旅行时没有发现违反条件)。
C++
// CPP program for the above approach #include <bits/stdc++.h> #include <iostream> using namespace std; class node { // A node class which stores the color and the edges // connected to the node public : int color = 1; set< int > edges; }; int canPaint(vector<node>& nodes, int n, int m) { // Create a visited array of n // nodes, initialized to zero vector< int > visited(n + 1, 0); // maxColors used till now are 1 as // all nodes are painted color 1 int maxColors = 1; // Do a full BFS traversal from // all unvisited starting points for ( int sv = 1; sv <= n; sv++) { if (visited[sv]) continue ; // If the starting point is unvisited, // mark it visited and push it in queue visited[sv] = 1; queue< int > q; q.push(sv); // BFS Travel starts here while (!q.empty()) { int top = q.front(); q.pop(); // Checking all adjacent nodes // to "top" edge in our queue for ( auto it = nodes[top].edges.begin(); it != nodes[top].edges.end(); it++) { // IMPORTANT: If the color of the // adjacent node is same, increase it by 1 if (nodes[top].color == nodes[*it].color) nodes[*it].color += 1; // If number of colors used shoots m, return // 0 maxColors = max(maxColors, max(nodes[top].color, nodes[*it].color)); if (maxColors > m) return 0; // If the adjacent node is not visited, // mark it visited and push it in queue if (!visited[*it]) { visited[*it] = 1; q.push(*it); } } } } return 1; } // Driver code int main() { int n = 4; bool graph[n][n] = { { 0, 1, 1, 1 }, { 1, 0, 1, 0 }, { 1, 1, 0, 1 }, { 1, 0, 1, 0 }}; int m = 3; // Number of colors // Create a vector of n+1 // nodes of type "node" // The zeroth position is just // dummy (1 to n to be used) vector<node> nodes(n + 1); // Add edges to each node as per given input for ( int i = 0; i < n; i++) { for ( int j =0;j<n;j++) { if (graph[i][j]) { // Connect the undirected graph nodes[i].edges.insert(i); nodes[j].edges.insert(j); } } } // Display final answer cout << canPaint(nodes, n, m); cout << "" ; return 0; } |
JAVA
// Java program for the above approach import java.io.*; import java.util.*; class Node { // A node class which stores the color and the edges // connected to the node int color = 1 ; Set<Integer> edges = new HashSet<Integer>(); } class GFG { static int canPaint(ArrayList<Node> nodes, int n, int m) { // Create a visited array of n // nodes, initialized to zero ArrayList<Integer> visited = new ArrayList<Integer>(); for ( int i = 0 ; i < n + 1 ; i++) { visited.add( 0 ); } // maxColors used till now are 1 as // all nodes are painted color 1 int maxColors = 1 ; // Do a full BFS traversal from // all unvisited starting points for ( int sv = 1 ; sv <= n; sv++) { if (visited.get(sv) > 0 ) { continue ; } // If the starting point is unvisited, // mark it visited and push it in queue visited.set(sv, 1 ); Queue<Integer> q = new LinkedList<>(); q.add(sv); // BFS Travel starts here while (q.size() != 0 ) { int top = q.peek(); q.remove(); // Checking all adjacent nodes // to "top" edge in our queue for ( int it: nodes.get(top).edges) { // IMPORTANT: If the color of the // adjacent node is same, increase it by 1 if (nodes.get(top).color == nodes.get(it).color) { nodes.get(it).color += 1 ; } // If number of colors used shoots m, return // 0 maxColors = Math.max(maxColors, Math.max(nodes.get(top).color, nodes.get(it).color)); if (maxColors > m) return 0 ; // If the adjacent node is not visited, // mark it visited and push it in queue if (visited.get(it) == 0 ) { visited.set(it, 1 ); q.remove(it); } } } } return 1 ; } // Driver code public static void main (String[] args) { int n = 4 ; int [][] graph = {{ 0 , 1 , 1 , 1 },{ 1 , 0 , 1 , 0 }, { 1 , 1 , 0 , 1 },{ 1 , 0 , 1 , 0 }}; int m = 3 ; // Number of colors // Create a vector of n+1 // nodes of type "node" // The zeroth position is just // dummy (1 to n to be used) ArrayList<Node> nodes = new ArrayList<Node>(); for ( int i = 0 ; i < n+ 1 ; i++) { nodes.add( new Node()); } // Add edges to each node as per given input for ( int i = 0 ; i < n; i++) { for ( int j = 0 ; j < n; j++) { if (graph[i][j] > 0 ) { // Connect the undirected graph nodes.get(i).edges.add(i); nodes.get(j).edges.add(j); } } } // Display final answer System.out.println(canPaint(nodes, n, m)); } } // This code is contributed by avanitrachhadiya2155 |
Python3
# Python3 program for the above approach from queue import Queue class node: color = 1 edges = set () def canPaint(nodes, n, m): # Create a visited array of n # nodes, initialized to zero visited = [ 0 for _ in range (n + 1 )] # maxColors used till now are 1 as # all nodes are painted color 1 maxColors = 1 # Do a full BFS traversal from # all unvisited starting points for _ in range ( 1 , n + 1 ): if visited[_]: continue # If the starting point is unvisited, # mark it visited and push it in queue visited[_] = 1 q = Queue() q.put(_) # BFS Travel starts here while not q.empty(): top = q.get() # Checking all adjacent nodes # to "top" edge in our queue for _ in nodes[top].edges: # IMPORTANT: If the color of the # adjacent node is same, increase it by 1 if nodes[top].color = = nodes[_].color: nodes[_].color + = 1 # If number of colors used shoots m, # return 0 maxColors = max (maxColors, max ( nodes[top].color, nodes[_].color)) if maxColors > m: print (maxColors) return 0 # If the adjacent node is not visited, # mark it visited and push it in queue if not visited[_]: visited[_] = 1 q.put(_) return 1 # Driver code if __name__ = = "__main__" : n = 4 graph = [ [ 0 , 1 , 1 , 1 ], [ 1 , 0 , 1 , 0 ], [ 1 , 1 , 0 , 1 ], [ 1 , 0 , 1 , 0 ] ] # Number of colors m = 3 # Create a vector of n+1 # nodes of type "node" # The zeroth position is just # dummy (1 to n to be used) nodes = [] for _ in range (n + 1 ): nodes.append(node()) # Add edges to each node as # per given input for _ in range (n): for __ in range (n): if graph[_][__]: # Connect the undirected graph nodes[_].edges.add(_) nodes[__].edges.add(__) # Display final answer print (canPaint(nodes, n, m)) # This code is contributed by harshitkap00r |
C#
// C# program for the above approach using System; using System.Collections; using System.Collections.Generic; class GFG { class node { // A node class which stores the color and the edges // connected to the node public int color = 1; public HashSet< int > edges = new HashSet< int >(); }; static int canPaint(List<node> nodes, int n, int m) { // Create a visited array of n // nodes, initialized to zero List< int > visited = new List< int >(); for ( int i = 0; i < n + 1; i++) { visited.Add(0); } // maxColors used till now are 1 as // all nodes are painted color 1 int maxColors = 1; // Do a full BFS traversal from // all unvisited starting points for ( int sv = 1; sv <= n; sv++) { if (visited[sv] > 0) continue ; // If the starting point is unvisited, // mark it visited and push it in queue visited[sv] = 1; Queue q = new Queue(); q.Enqueue(sv); // BFS Travel starts here while (q.Count != 0) { int top = ( int )q.Peek(); q.Dequeue(); // Checking all adjacent nodes // to "top" edge in our queue foreach ( int it in nodes[top].edges) { // IMPORTANT: If the color of the // adjacent node is same, increase it by 1 if (nodes[top].color == nodes[it].color) nodes[it].color += 1; // If number of colors used shoots m, return // 0 maxColors = Math.Max(maxColors, Math.Max(nodes[top].color, nodes[it].color)); if (maxColors > m) return 0; // If the adjacent node is not visited, // mark it visited and push it in queue if (visited[it] == 0) { visited[it] = 1; q.Enqueue(it); } } } } return 1; } // Driver code public static void Main() { int n = 4; int [,]graph = { { 0, 1, 1, 1 }, { 1, 0, 1, 0 }, { 1, 1, 0, 1 }, { 1, 0, 1, 0 }}; int m = 3; // Number of colors // Create a vector of n+1 // nodes of type "node" // The zeroth position is just // dummy (1 to n to be used) List<node> nodes = new List<node>(); for ( int i = 0; i < n+ 1; i++) { nodes.Add( new node()); } // Add edges to each node as per given input for ( int i = 0; i < n; i++) { for ( int j = 0; j < n; j++) { if (graph[i, j] > 0) { // Connect the undirected graph nodes[i].edges.Add(i); nodes[j].edges.Add(j); } } } // Display final answer Console.WriteLine(canPaint(nodes, n, m)); } } // This code is contributed by rutvik_56. |
Javascript
<script> // Javascript program for the above approach class node { // A node class which stores the color // and the edges connected to the node constructor() { this .color = 1; this .edges = new Set(); } }; function canPaint(nodes, n, m) { // Create a visited array of n // nodes, initialized to zero var visited = []; for ( var i = 0; i < n + 1; i++) { visited.push(0); } // maxColors used till now are 1 as // all nodes are painted color 1 var maxColors = 1; // Do a full BFS traversal from // all unvisited starting points for ( var sv = 1; sv <= n; sv++) { if (visited[sv] > 0) continue ; // If the starting point is unvisited, // mark it visited and push it in queue visited[sv] = 1; var q = []; q.push(sv); // BFS Travel starts here while (q.length != 0) { var top = q[0]; q.shift(); // Checking all adjacent nodes // to "top" edge in our queue for ( var it of nodes[top].edges) { // IMPORTANT: If the color of the // adjacent node is same, increase it by 1 if (nodes[top].color == nodes[it].color) nodes[it].color += 1; // If number of colors used shoots m, return // 0 maxColors = Math.max(maxColors, Math.max( nodes[top].color, nodes[it].color)); if (maxColors > m) return 0; // If the adjacent node is not visited, // mark it visited and push it in queue if (visited[it] == 0) { visited[it] = 1; q.push(it); } } } } return 1; } // Driver code var n = 4; var graph = [ [ 0, 1, 1, 1 ], [ 1, 0, 1, 0 ], [ 1, 1, 0, 1 ], [ 1, 0, 1, 0 ] ]; // Number of colors var m = 3; // Create a vector of n+1 // nodes of type "node" // The zeroth position is just // dummy (1 to n to be used) var nodes = []; for ( var i = 0; i < n+ 1; i++) { nodes.push( new node()); } // Push edges to each node as per given input for ( var i = 0; i < n; i++) { for ( var j = 0; j < n; j++) { if (graph[i, j] > 0) { // Connect the undirected graph nodes[i].edges.push(i); nodes[j].edges.push(j); } } } // Display final answer document.write(canPaint(nodes, n, m)); // This code is contributed by rrrtnx </script> |
1
复杂性分析:
- 时间复杂性: O(V+E)。
- 空间复杂性: O(V)。用于存储访问列表。
参考资料: http://en.wikipedia.org/wiki/Graph_coloring 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



