我们讨论了重叠子问题和最优子结构性质 第一组 和 第二组 分别地我们还讨论了中的一个示例问题 第三组 .让我们讨论最长公共子序列(LCS)问题,作为可以使用动态规划解决的又一个示例问题。
LCS问题声明: 给定两个序列,求两个序列中最长子序列的长度。子序列是以相同的相对顺序出现的序列,但不一定是连续的。例如,“abc”、“abg”、“bdf”、“aeg”、“acefg”。。etc是“abcdefg”的子序列。
为了找出蛮力方法的复杂性,我们首先需要知道长度为n的字符串可能不同的子序列的数量,也就是说,找到长度为1,2,。。n-1。回想一下置换和组合理论,1个元素的组合数是 N C 1. .包含2个元素的组合数为 N C 2. 等等等等。我们知道 N C 0 + N C 1. + N C 2. + … N C N = 2 N 所以长度为n的字符串有2 N – 1个不同的可能子序列,因为我们不考虑长度为0的子序列。这意味着蛮力方法的时间复杂度为O(n*2) N ).请注意,检查两个字符串是否共用一个子序列需要O(n)时间。这种时间复杂性可以通过使用动态规划来提高。
这是一个经典的计算机科学问题,是计算机科学的基础 差别 (输出两个文件之间差异的文件比较程序),并在生物信息学中有应用。
例如: 输入序列“ABCDGH”和“AEDFHR”的LCS是长度为3的“ADH”。 输入序列“AGGTAB”和“GXTXAYB”的LCS是长度为4的“GTAB”。
该问题的简单解决方案是生成两个给定序列的所有子序列,并找到最长的匹配子序列。这个解决方案的时间复杂度是指数的。让我们看看这个问题如何同时具有动态规划(DP)问题的两个重要性质。
1) 最佳子结构: 设输入序列分别为长度为m和n的X[0..m-1]和Y[0..n-1]。设L(X[0..m-1],Y[0..n-1])是两个序列X和Y的LCS的长度。下面是L(X[0..m-1],Y[0..n-1])的递归定义。
如果两个序列的最后一个字符匹配(或X[m-1]==Y[n-1]),则 L(X[0..m-1],Y[0..n-1])=1+L(X[0..m-2],Y[0..n-2])
如果两个序列的最后一个字符不匹配(或X[m-1]!=Y[n-1]),则 L(X[0..m-1],Y[0..n-1])=MAX(L(X[0..m-2],Y[0..n-1]),L(X[0..m-1],Y[0..n-2]))
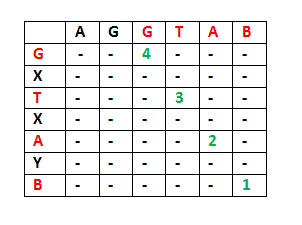
例如: 1)考虑输入字符串“AgPaTb”和“GXTXAYB”。最后一个字符与字符串匹配。因此,LCS的长度可以写为: L(“AGGTAB”、“GXTXAYB”)=1+L(“AGGTA”、“GXTXAY”)
2)考虑输入字符串“ABCDGH”和“AEDFHR”。最后的字符与字符串不匹配。因此,LCS的长度可以写成: L(“ABCDGH”、“AEDFHR”)=MAX(L(“ABCDG”、“AEDFH R (“ABCDG H “,“AEDFH”)) 因此,LCS问题具有最优子结构性质,因为主要问题可以用子问题的解来解决。
2) 重叠子问题: 下面是LCS问题的简单递归实现。实现简单地遵循上面提到的递归结构。
C++
/* A Naive recursive implementation of LCS problem */ #include <bits/stdc++.h> using namespace std; /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ int lcs( char *X, char *Y, int m, int n ) { if (m == 0 || n == 0) return 0; if (X[m-1] == Y[n-1]) return 1 + lcs(X, Y, m-1, n-1); else return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n)); } /* Driver code */ int main() { char X[] = "AGGTAB" ; char Y[] = "GXTXAYB" ; int m = strlen (X); int n = strlen (Y); cout<< "Length of LCS is " << lcs( X, Y, m, n ) ; return 0; } // This code is contributed by rathbhupendra |
C
/* A Naive recursive implementation of LCS problem */ #include<bits/stdc++.h> int max( int a, int b); /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ int lcs( char *X, char *Y, int m, int n ) { if (m == 0 || n == 0) return 0; if (X[m-1] == Y[n-1]) return 1 + lcs(X, Y, m-1, n-1); else return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n)); } /* Utility function to get max of 2 integers */ int max( int a, int b) { return (a > b)? a : b; } /* Driver program to test above function */ int main() { char X[] = "AGGTAB" ; char Y[] = "GXTXAYB" ; int m = strlen (X); int n = strlen (Y); printf ( "Length of LCS is %d" , lcs( X, Y, m, n ) ); return 0; } |
JAVA
/* A Naive recursive implementation of LCS problem in java*/ public class LongestCommonSubsequence { /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ int lcs( char [] X, char [] Y, int m, int n ) { if (m == 0 || n == 0 ) return 0 ; if (X[m- 1 ] == Y[n- 1 ]) return 1 + lcs(X, Y, m- 1 , n- 1 ); else return max(lcs(X, Y, m, n- 1 ), lcs(X, Y, m- 1 , n)); } /* Utility function to get max of 2 integers */ int max( int a, int b) { return (a > b)? a : b; } public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence(); String s1 = "AGGTAB" ; String s2 = "GXTXAYB" ; char [] X=s1.toCharArray(); char [] Y=s2.toCharArray(); int m = X.length; int n = Y.length; System.out.println( "Length of LCS is" + " " + lcs.lcs( X, Y, m, n ) ); } } // This Code is Contributed by Saket Kumar |
Python3
# A Naive recursive Python implementation of LCS problem def lcs(X, Y, m, n): if m = = 0 or n = = 0 : return 0 elif X[m - 1 ] = = Y[n - 1 ]: return 1 + lcs(X, Y, m - 1 , n - 1 ); else : return max (lcs(X, Y, m, n - 1 ), lcs(X, Y, m - 1 , n)); # Driver program to test the above function X = "AGGTAB" Y = "GXTXAYB" print ( "Length of LCS is " , lcs(X , Y, len (X), len (Y)) ) |
C#
/* C# Naive recursive implementation of LCS problem */ using System; class GFG { /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ static int lcs( char [] X, char [] Y, int m, int n ) { if (m == 0 || n == 0) return 0; if (X[m - 1] == Y[n - 1]) return 1 + lcs(X, Y, m - 1, n - 1); else return max(lcs(X, Y, m, n - 1), lcs(X, Y, m - 1, n)); } /* Utility function to get max of 2 integers */ static int max( int a, int b) { return (a > b)? a : b; } public static void Main() { String s1 = "AGGTAB" ; String s2 = "GXTXAYB" ; char [] X=s1.ToCharArray(); char [] Y=s2.ToCharArray(); int m = X.Length; int n = Y.Length; Console.Write( "Length of LCS is" + " " +lcs( X, Y, m, n ) ); } } // This code is Contributed by Sam007 |
PHP
<?php // A Naive recursive PHP // implementation of LCS problem function lcs( $X , $Y , $m , $n ) { if ( $m == 0 || $n == 0) return 0; else if ( $X [ $m - 1] == $Y [ $n - 1]) return 1 + lcs( $X , $Y , $m - 1, $n - 1); else return max(lcs( $X , $Y , $m , $n - 1), lcs( $X , $Y , $m - 1, $n )); } // Driver Code $X = "AGGTAB" ; $Y = "GXTXAYB" ; echo "Length of LCS is " ; echo lcs( $X , $Y , strlen ( $X ), strlen ( $Y )); // This code is contributed // by Shivi_Aggarwal ?> |
Javascript
<script> /* A Naive recursive implementation of LCS problem in java*/ /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ function lcs( X, Y , m , n ) { if (m == 0 || n == 0) return 0; if (X[m-1] == Y[n-1]) return 1 + lcs(X, Y, m-1, n-1); else return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n)); } /* Utility function to get max of 2 integers */ function max(a , b) { return (a > b)? a : b; } var s1 = "AGGTAB" ; var s2 = "GXTXAYB" ; var X=s1; var Y=s2; var m = X.length; var n = Y.length; document.write( "Length of LCS is" + " " + lcs( X, Y, m, n ) ); // This code contributed by umadevi9616 </script> |
输出:
Length of LCS is 4
在最坏情况下,上述朴素递归方法的时间复杂度为O(2^n),最坏情况发生在X和Y的所有字符不匹配时,即LCS的长度为0。
考虑到上述实现,下面是输入字符串“AXYT”和“AYZX”的部分递归树
lcs("AXYT", "AYZX") / lcs("AXY", "AYZX") lcs("AXYT", "AYZ") / / lcs("AX", "AYZX") lcs("AXY", "AYZ") lcs("AXY", "AYZ") lcs("AXYT", "AY")
在上面的部分递归树中,lcs(“AXY”、“AYZ”)将被求解两次。如果我们画出完整的递归树,那么我们可以看到有许多子问题被一次又一次地解决。因此,该问题具有重叠子结构的性质,通过记忆或制表可以避免相同子问题的重新计算。以下是LCS问题的列表实现。
Python3
def lcs(s1 , s2): m, n = len (s1), len (s2) prev, cur = [ 0 ] * (n + 1 ), [ 0 ] * (n + 1 ) for i in range ( 1 , m + 1 ): for j in range ( 1 , n + 1 ): if s1[i - 1 ] = = s2[j - 1 ]: cur[j] = 1 + prev[j - 1 ] else : if cur[j - 1 ] > prev[j]: cur[j] = cur[j - 1 ] else : cur[j] = prev[j] cur, prev = prev, cur return prev[n] #end of function lcs # Driver program to test the above function s1 = "AGGTAB" s2 = "GXTXAYB" print ( "Length of LCS is " , lcs(s1, s2)) # BY PRASHANT SHEKHAR MISHRA |
C
/* Dynamic Programming C implementation of LCS problem */ #include<bits/stdc++.h> int max( int a, int b); /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ int lcs( char *X, char *Y, int m, int n ) { int L[m+1][n+1]; int i, j; /* Following steps build L[m+1][n+1] in bottom up fashion. Note that L[i][j] contains length of LCS of X[0..i-1] and Y[0..j-1] */ for (i=0; i<=m; i++) { for (j=0; j<=n; j++) { if (i == 0 || j == 0) L[i][j] = 0; else if (X[i-1] == Y[j-1]) L[i][j] = L[i-1][j-1] + 1; else L[i][j] = max(L[i-1][j], L[i][j-1]); } } /* L[m][n] contains length of LCS for X[0..n-1] and Y[0..m-1] */ return L[m][n]; } /* Utility function to get max of 2 integers */ int max( int a, int b) { return (a > b)? a : b; } /* Driver program to test above function */ int main() { char X[] = "AGGTAB" ; char Y[] = "GXTXAYB" ; int m = strlen (X); int n = strlen (Y); printf ( "Length of LCS is %d" , lcs( X, Y, m, n ) ); return 0; } |
JAVA
/* Dynamic Programming Java implementation of LCS problem */ public class LongestCommonSubsequence { /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ int lcs( char [] X, char [] Y, int m, int n ) { int L[][] = new int [m+ 1 ][n+ 1 ]; /* Following steps build L[m+1][n+1] in bottom up fashion. Note that L[i][j] contains length of LCS of X[0..i-1] and Y[0..j-1] */ for ( int i= 0 ; i<=m; i++) { for ( int j= 0 ; j<=n; j++) { if (i == 0 || j == 0 ) L[i][j] = 0 ; else if (X[i- 1 ] == Y[j- 1 ]) L[i][j] = L[i- 1 ][j- 1 ] + 1 ; else L[i][j] = max(L[i- 1 ][j], L[i][j- 1 ]); } } return L[m][n]; } /* Utility function to get max of 2 integers */ int max( int a, int b) { return (a > b)? a : b; } public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence(); String s1 = "AGGTAB" ; String s2 = "GXTXAYB" ; char [] X=s1.toCharArray(); char [] Y=s2.toCharArray(); int m = X.length; int n = Y.length; System.out.println( "Length of LCS is" + " " + lcs.lcs( X, Y, m, n ) ); } } // This Code is Contributed by Saket Kumar |
Python3
# Dynamic Programming implementation of LCS problem def lcs(X , Y): # find the length of the strings m = len (X) n = len (Y) # declaring the array for storing the dp values L = [[ None ] * (n + 1 ) for i in range (m + 1 )] """Following steps build L[m+1][n+1] in bottom up fashion Note: L[i][j] contains length of LCS of X[0..i-1] and Y[0..j-1]""" for i in range (m + 1 ): for j in range (n + 1 ): if i = = 0 or j = = 0 : L[i][j] = 0 elif X[i - 1 ] = = Y[j - 1 ]: L[i][j] = L[i - 1 ][j - 1 ] + 1 else : L[i][j] = max (L[i - 1 ][j] , L[i][j - 1 ]) # L[m][n] contains the length of LCS of X[0..n-1] & Y[0..m-1] return L[m][n] #end of function lcs # Driver program to test the above function X = "AGGTAB" Y = "GXTXAYB" print ( "Length of LCS is " , lcs(X, Y) ) # This code is contributed by Nikhil Kumar Singh(nickzuck_007) |
C#
// Dynamic Programming C# implementation // of LCS problem using System; class GFG { /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ static int lcs( char [] X, char [] Y, int m, int n ) { int [,]L = new int [m+1,n+1]; /* Following steps build L[m+1][n+1] in bottom up fashion. Note that L[i][j] contains length of LCS of X[0..i-1] and Y[0..j-1] */ for ( int i = 0; i <= m; i++) { for ( int j = 0; j <= n; j++) { if (i == 0 || j == 0) L[i, j] = 0; else if (X[i - 1] == Y[j - 1]) L[i, j] = L[i - 1, j - 1] + 1; else L[i, j] = max(L[i - 1, j], L[i, j - 1]); } } return L[m, n]; } /* Utility function to get max of 2 integers */ static int max( int a, int b) { return (a > b)? a : b; } // Driver code public static void Main() { String s1 = "AGGTAB" ; String s2 = "GXTXAYB" ; char [] X=s1.ToCharArray(); char [] Y=s2.ToCharArray(); int m = X.Length; int n = Y.Length; Console.Write( "Length of LCS is" + " " +lcs( X, Y, m, n ) ); } } // This Code is Contributed by Sam007 |
PHP
<?php // Dynamic Programming C# // implementation of LCS problem function lcs( $X , $Y ) { // find the length of the strings $m = strlen ( $X ); $n = strlen ( $Y ) ; // declaring the array for // storing the dp values /*Following steps build L[m+1][n+1] in bottom up fashion . Note: L[i][j] contains length of LCS of X[0..i-1] and Y[0..j-1] */ for ( $i = 0; $i <= $m ; $i ++) { for ( $j = 0; $j <= $n ; $j ++) { if ( $i == 0 || $j == 0) $L [ $i ][ $j ] = 0; else if ( $X [ $i - 1] == $Y [ $j - 1]) $L [ $i ][ $j ] = $L [ $i - 1][ $j - 1] + 1; else $L [ $i ][ $j ] = max( $L [ $i - 1][ $j ], $L [ $i ][ $j - 1]); } } // L[m][n] contains the length of // LCS of X[0..n-1] & Y[0..m-1] return $L [ $m ][ $n ]; } // Driver Code $X = "AGGTAB" ; $Y = "GXTXAYB" ; echo "Length of LCS is " ; echo lcs( $X , $Y ); // This code is contributed // by Shivi_Aggarwal ?> |
Javascript
<script> // Dynamic Programming Java implementation of LCS problem // Utility function to get max of 2 integers function max(a, b) { if (a > b) return a; else return b; } // Returns length of LCS for X[0..m-1], Y[0..n-1] function lcs(X, Y, m, n) { var L = new Array(m + 1); for ( var i = 0; i < L.length; i++) { L[i] = new Array(n + 1); } var i, j; /* Following steps build L[m+1][n+1] in bottom up fashion. Note that L[i][j] contains length of LCS of X[0..i-1] and Y[0..j-1] */ for (i = 0; i <= m; i++) { for (j = 0; j <= n; j++) { if (i == 0 || j == 0) L[i][j] = 0; else if (X[i - 1] == Y[j - 1]) L[i][j] = L[i - 1][j - 1] + 1; else L[i][j] = max(L[i - 1][j], L[i][j - 1]); } } /* L[m][n] contains length of LCS for X[0..n-1] and Y[0..m-1] */ return L[m][n]; } // Driver code var x = "AGGTAB" ; var y = "GXTXAYB" ; var m = x.length; var n = y.length; document.write( "Length of LCS is " + lcs(x, y, m, n)); // This code is contributed by akshitsaxenaa09 </script> |
输出:
Length of LCS is 4
上述实现的时间复杂度为O(mn),这比朴素递归实现的最坏情况下的时间复杂度要好得多。 上述算法/代码只返回LCS的长度。请参阅下面的帖子来打印LCS。 打印最长公共子序列 您还可以在以下位置查看LCS的空间优化版本: LCS的空间优化解
如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。 最近基于LCS的文章!
参考资料: http://www.youtube.com/watch?v=V5hZoJ6uK-s http://www.algorithmist.com/index.php/Longest_Common_Subsequence http://www.ics.uci.edu/~eppstein/161/960229。html http://en.wikipedia.org/wiki/Longest_common_subsequence_problem


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



