回溯是一种算法范例,尝试不同的解决方案,直到找到一个“有效”的解决方案。通常使用回溯技术解决的问题具有以下共同特性。这些问题只能通过尝试每种可能的配置来解决,并且每种配置只尝试一次。对于这些问题,一个简单的解决方案是尝试所有配置,并输出符合给定问题约束的配置。回溯是一种渐进式的工作方式,是对原始解决方案的优化,所有可能的配置都会生成并尝试。 例如,考虑以下内容 骑士之旅 问题
问题陈述: 给出一个N*N的棋盘,骑士被放在一块空棋盘的第一块上。按照国际象棋规则移动的骑士必须精确地访问每个广场一次。打印每个单元格的访问顺序。
例子:
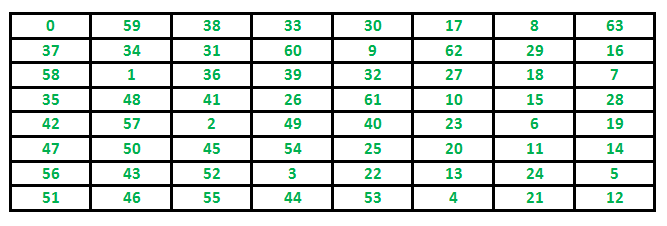
Input : N = 8Output:0 59 38 33 30 17 8 6337 34 31 60 9 62 29 1658 1 36 39 32 27 18 735 48 41 26 61 10 15 2842 57 2 49 40 23 6 1947 50 45 54 25 20 11 1456 43 52 3 22 13 24 551 46 55 44 53 4 21 12
骑士走过的道路覆盖了所有的牢房 下面是一个有8 x 8个单元格的棋盘。单元格中的数字表示骑士的移动编号。
让我们先讨论这个问题的朴素算法,然后再讨论回溯算法。
骑士之旅的朴素算法 朴素算法是逐个生成所有巡更,并检查生成的巡更是否满足约束。
while there are untried tours{ generate the next tour if this tour covers all squares { print this path; }}
回溯 以渐进的方式解决问题。通常,我们从一个空的解决方案向量开始,逐个添加项目(项目的含义因问题而异。在骑士巡演问题的上下文中,项目是骑士的移动)。当我们添加一个项目时,我们会检查添加当前项目是否违反了问题约束,如果违反了问题约束,那么我们会删除该项目并尝试其他替代方案。如果没有一个替代方案可行,那么我们进入前一阶段,删除前一阶段中添加的项目。如果我们回到最初的阶段,那么我们说不存在解决方案。如果添加一个项目没有违反约束,那么我们会递归地逐个添加项目。如果解向量变得完整,那么我们打印解。
骑士巡演的回溯算法
下面是骑士之旅问题的回溯算法。
If all squares are visited print the solutionElse a) Add one of the next moves to solution vector and recursively check if this move leads to a solution. (A Knight can make maximum eight moves. We choose one of the 8 moves in this step). b) If the move chosen in the above step doesn't lead to a solution then remove this move from the solution vector and try other alternative moves. c) If none of the alternatives work then return false (Returning false will remove the previously added item in recursion and if false is returned by the initial call of recursion then "no solution exists" )
以下是骑士之旅问题的实现。它以2D矩阵形式打印一个可能的解决方案。基本上,输出是一个2D 8*8矩阵,数字从0到63,这些数字显示了Knight的步骤。
C++
// C++ program for Knight Tour problem #include <bits/stdc++.h> using namespace std; #define N 8 int solveKTUtil( int x, int y, int movei, int sol[N][N], int xMove[], int yMove[]); /* A utility function to check if i,j are valid indexes for N*N chessboard */ int isSafe( int x, int y, int sol[N][N]) { return (x >= 0 && x < N && y >= 0 && y < N && sol[x][y] == -1); } /* A utility function to print solution matrix sol[N][N] */ void printSolution( int sol[N][N]) { for ( int x = 0; x < N; x++) { for ( int y = 0; y < N; y++) cout << " " << setw(2) << sol[x][y] << " " ; cout << endl; } } /* This function solves the Knight Tour problem using Backtracking. This function mainly uses solveKTUtil() to solve the problem. It returns false if no complete tour is possible, otherwise return true and prints the tour. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int solveKT() { int sol[N][N]; /* Initialization of solution matrix */ for ( int x = 0; x < N; x++) for ( int y = 0; y < N; y++) sol[x][y] = -1; /* xMove[] and yMove[] define next move of Knight. xMove[] is for next value of x coordinate yMove[] is for next value of y coordinate */ int xMove[8] = { 2, 1, -1, -2, -2, -1, 1, 2 }; int yMove[8] = { 1, 2, 2, 1, -1, -2, -2, -1 }; // Since the Knight is initially at the first block sol[0][0] = 0; /* Start from 0,0 and explore all tours using solveKTUtil() */ if (solveKTUtil(0, 0, 1, sol, xMove, yMove) == 0) { cout << "Solution does not exist" ; return 0; } else printSolution(sol); return 1; } /* A recursive utility function to solve Knight Tour problem */ int solveKTUtil( int x, int y, int movei, int sol[N][N], int xMove[8], int yMove[8]) { int k, next_x, next_y; if (movei == N * N) return 1; /* Try all next moves from the current coordinate x, y */ for (k = 0; k < 8; k++) { next_x = x + xMove[k]; next_y = y + yMove[k]; if (isSafe(next_x, next_y, sol)) { sol[next_x][next_y] = movei; if (solveKTUtil(next_x, next_y, movei + 1, sol, xMove, yMove) == 1) return 1; else // backtracking sol[next_x][next_y] = -1; } } return 0; } // Driver Code int main() { // Function Call solveKT(); return 0; } // This code is contributed by ShubhamCoder |
C
// C program for Knight Tour problem #include <stdio.h> #define N 8 int solveKTUtil( int x, int y, int movei, int sol[N][N], int xMove[], int yMove[]); /* A utility function to check if i,j are valid indexes for N*N chessboard */ int isSafe( int x, int y, int sol[N][N]) { return (x >= 0 && x < N && y >= 0 && y < N && sol[x][y] == -1); } /* A utility function to print solution matrix sol[N][N] */ void printSolution( int sol[N][N]) { for ( int x = 0; x < N; x++) { for ( int y = 0; y < N; y++) printf ( " %2d " , sol[x][y]); printf ( "" ); } } /* This function solves the Knight Tour problem using Backtracking. This function mainly uses solveKTUtil() to solve the problem. It returns false if no complete tour is possible, otherwise return true and prints the tour. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int solveKT() { int sol[N][N]; /* Initialization of solution matrix */ for ( int x = 0; x < N; x++) for ( int y = 0; y < N; y++) sol[x][y] = -1; /* xMove[] and yMove[] define next move of Knight. xMove[] is for next value of x coordinate yMove[] is for next value of y coordinate */ int xMove[8] = { 2, 1, -1, -2, -2, -1, 1, 2 }; int yMove[8] = { 1, 2, 2, 1, -1, -2, -2, -1 }; // Since the Knight is initially at the first block sol[0][0] = 0; /* Start from 0,0 and explore all tours using solveKTUtil() */ if (solveKTUtil(0, 0, 1, sol, xMove, yMove) == 0) { printf ( "Solution does not exist" ); return 0; } else printSolution(sol); return 1; } /* A recursive utility function to solve Knight Tour problem */ int solveKTUtil( int x, int y, int movei, int sol[N][N], int xMove[N], int yMove[N]) { int k, next_x, next_y; if (movei == N * N) return 1; /* Try all next moves from the current coordinate x, y */ for (k = 0; k < 8; k++) { next_x = x + xMove[k]; next_y = y + yMove[k]; if (isSafe(next_x, next_y, sol)) { sol[next_x][next_y] = movei; if (solveKTUtil(next_x, next_y, movei + 1, sol, xMove, yMove) == 1) return 1; else sol[next_x][next_y] = -1; // backtracking } } return 0; } /* Driver Code */ int main() { // Function Call solveKT(); return 0; } |
JAVA
// Java program for Knight Tour problem class KnightTour { static int N = 8 ; /* A utility function to check if i,j are valid indexes for N*N chessboard */ static boolean isSafe( int x, int y, int sol[][]) { return (x >= 0 && x < N && y >= 0 && y < N && sol[x][y] == - 1 ); } /* A utility function to print solution matrix sol[N][N] */ static void printSolution( int sol[][]) { for ( int x = 0 ; x < N; x++) { for ( int y = 0 ; y < N; y++) System.out.print(sol[x][y] + " " ); System.out.println(); } } /* This function solves the Knight Tour problem using Backtracking. This function mainly uses solveKTUtil() to solve the problem. It returns false if no complete tour is possible, otherwise return true and prints the tour. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ static boolean solveKT() { int sol[][] = new int [ 8 ][ 8 ]; /* Initialization of solution matrix */ for ( int x = 0 ; x < N; x++) for ( int y = 0 ; y < N; y++) sol[x][y] = - 1 ; /* xMove[] and yMove[] define next move of Knight. xMove[] is for next value of x coordinate yMove[] is for next value of y coordinate */ int xMove[] = { 2 , 1 , - 1 , - 2 , - 2 , - 1 , 1 , 2 }; int yMove[] = { 1 , 2 , 2 , 1 , - 1 , - 2 , - 2 , - 1 }; // Since the Knight is initially at the first block sol[ 0 ][ 0 ] = 0 ; /* Start from 0,0 and explore all tours using solveKTUtil() */ if (!solveKTUtil( 0 , 0 , 1 , sol, xMove, yMove)) { System.out.println( "Solution does not exist" ); return false ; } else printSolution(sol); return true ; } /* A recursive utility function to solve Knight Tour problem */ static boolean solveKTUtil( int x, int y, int movei, int sol[][], int xMove[], int yMove[]) { int k, next_x, next_y; if (movei == N * N) return true ; /* Try all next moves from the current coordinate x, y */ for (k = 0 ; k < 8 ; k++) { next_x = x + xMove[k]; next_y = y + yMove[k]; if (isSafe(next_x, next_y, sol)) { sol[next_x][next_y] = movei; if (solveKTUtil(next_x, next_y, movei + 1 , sol, xMove, yMove)) return true ; else sol[next_x][next_y] = - 1 ; // backtracking } } return false ; } /* Driver Code */ public static void main(String args[]) { // Function Call solveKT(); } } // This code is contributed by Abhishek Shankhadhar |
Python3
# Python3 program to solve Knight Tour problem using Backtracking # Chessboard Size n = 8 def isSafe(x, y, board): ''' A utility function to check if i,j are valid indexes for N*N chessboard ''' if (x > = 0 and y > = 0 and x < n and y < n and board[x][y] = = - 1 ): return True return False def printSolution(n, board): ''' A utility function to print Chessboard matrix ''' for i in range (n): for j in range (n): print (board[i][j], end = ' ' ) print () def solveKT(n): ''' This function solves the Knight Tour problem using Backtracking. This function mainly uses solveKTUtil() to solve the problem. It returns false if no complete tour is possible, otherwise return true and prints the tour. Please note that there may be more than one solutions, this function prints one of the feasible solutions. ''' # Initialization of Board matrix board = [[ - 1 for i in range (n)] for i in range (n)] # move_x and move_y define next move of Knight. # move_x is for next value of x coordinate # move_y is for next value of y coordinate move_x = [ 2 , 1 , - 1 , - 2 , - 2 , - 1 , 1 , 2 ] move_y = [ 1 , 2 , 2 , 1 , - 1 , - 2 , - 2 , - 1 ] # Since the Knight is initially at the first block board[ 0 ][ 0 ] = 0 # Step counter for knight's position pos = 1 # Checking if solution exists or not if ( not solveKTUtil(n, board, 0 , 0 , move_x, move_y, pos)): print ( "Solution does not exist" ) else : printSolution(n, board) def solveKTUtil(n, board, curr_x, curr_y, move_x, move_y, pos): ''' A recursive utility function to solve Knight Tour problem ''' if (pos = = n * * 2 ): return True # Try all next moves from the current coordinate x, y for i in range ( 8 ): new_x = curr_x + move_x[i] new_y = curr_y + move_y[i] if (isSafe(new_x, new_y, board)): board[new_x][new_y] = pos if (solveKTUtil(n, board, new_x, new_y, move_x, move_y, pos + 1 )): return True # Backtracking board[new_x][new_y] = - 1 return False # Driver Code if __name__ = = "__main__" : # Function Call solveKT(n) # This code is contributed by AAKASH PAL |
C#
// C# program for // Knight Tour problem using System; class GFG { static int N = 8; /* A utility function to check if i,j are valid indexes for N*N chessboard */ static bool isSafe( int x, int y, int [, ] sol) { return (x >= 0 && x < N && y >= 0 && y < N && sol[x, y] == -1); } /* A utility function to print solution matrix sol[N][N] */ static void printSolution( int [, ] sol) { for ( int x = 0; x < N; x++) { for ( int y = 0; y < N; y++) Console.Write(sol[x, y] + " " ); Console.WriteLine(); } } /* This function solves the Knight Tour problem using Backtracking. This function mainly uses solveKTUtil() to solve the problem. It returns false if no complete tour is possible, otherwise return true and prints the tour. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ static bool solveKT() { int [, ] sol = new int [8, 8]; /* Initialization of solution matrix */ for ( int x = 0; x < N; x++) for ( int y = 0; y < N; y++) sol[x, y] = -1; /* xMove[] and yMove[] define next move of Knight. xMove[] is for next value of x coordinate yMove[] is for next value of y coordinate */ int [] xMove = { 2, 1, -1, -2, -2, -1, 1, 2 }; int [] yMove = { 1, 2, 2, 1, -1, -2, -2, -1 }; // Since the Knight is // initially at the first block sol[0, 0] = 0; /* Start from 0,0 and explore all tours using solveKTUtil() */ if (!solveKTUtil(0, 0, 1, sol, xMove, yMove)) { Console.WriteLine( "Solution does " + "not exist" ); return false ; } else printSolution(sol); return true ; } /* A recursive utility function to solve Knight Tour problem */ static bool solveKTUtil( int x, int y, int movei, int [, ] sol, int [] xMove, int [] yMove) { int k, next_x, next_y; if (movei == N * N) return true ; /* Try all next moves from the current coordinate x, y */ for (k = 0; k < 8; k++) { next_x = x + xMove[k]; next_y = y + yMove[k]; if (isSafe(next_x, next_y, sol)) { sol[next_x, next_y] = movei; if (solveKTUtil(next_x, next_y, movei + 1, sol, xMove, yMove)) return true ; else // backtracking sol[next_x, next_y] = -1; } } return false ; } // Driver Code public static void Main() { // Function Call solveKT(); } } // This code is contributed by mits. |
Javascript
<script> // Javascript program for Knight Tour problem let N = 8; // A utility function to check if i,j are // valid indexes for N*N chessboard function isSafe(x, y, sol) { return (x >= 0 && x < N && y >= 0 && y < N && sol[x][y] == -1); } // A utility function to print solution // matrix sol[N][N] function printSolution(sol) { for (let x = 0; x < N; x++) { for (let y = 0; y < N; y++) document.write(sol[x][y] + " " ); document.write( "<br/>" ); } } // This function solves the Knight Tour problem // using Backtracking. This function mainly // uses solveKTUtil() to solve the problem. It // returns false if no complete tour is possible, // otherwise return true and prints the tour. // Please note that there may be more than one // solutions, this function prints one of the // feasible solutions. function solveKT() { let sol = new Array(8); for ( var i = 0; i < sol.length; i++) { sol[i] = new Array(2); } // Initialization of solution matrix for (let x = 0; x < N; x++) for (let y = 0; y < N; y++) sol[x][y] = -1; // xMove[] and yMove[] define next move of Knight. // xMove[] is for next value of x coordinate // yMove[] is for next value of y coordinate let xMove = [ 2, 1, -1, -2, -2, -1, 1, 2 ]; let yMove = [ 1, 2, 2, 1, -1, -2, -2, -1 ]; // Since the Knight is initially at the first block sol[0][0] = 0; // Start from 0,0 and explore all tours using // solveKTUtil() if (!solveKTUtil(0, 0, 1, sol, xMove, yMove)) { document.write( "Solution does not exist" ); return false ; } else printSolution(sol); return true ; } // A recursive utility function to solve Knight // Tour problem function solveKTUtil(x, y, movei, sol, xMove, yMove) { let k, next_x, next_y; if (movei == N * N) return true ; // Try all next moves from the // current coordinate x, y for (k = 0; k < 8; k++) { next_x = x + xMove[k]; next_y = y + yMove[k]; if (isSafe(next_x, next_y, sol)) { sol[next_x][next_y] = movei; if (solveKTUtil(next_x, next_y, movei + 1, sol, xMove, yMove)) return true ; else sol[next_x][next_y] = -1; // backtracking } } return false ; } // Driver code // Function Call solveKT(); // This code is contributed by target_2 </script> |
0 59 38 33 30 17 8 63 37 34 31 60 9 62 29 16 58 1 36 39 32 27 18 7 35 48 41 26 61 10 15 28 42 57 2 49 40 23 6 19 47 50 45 54 25 20 11 14 56 43 52 3 22 13 24 5 51 46 55 44 53 4 21 12
时间复杂性: 有N个 2. 对于每个单元格,我们最多可以选择8个移动,所以最糟糕的运行时间是O(8) N^2 ).
辅助空间: O(N) 2. )
重要提示: xMove和yMove的顺序都是错误的,但它们会极大地影响算法的运行时间。例如,考虑这样一种情况:第八次选择的移动是正确的,在此之前,我们的代码运行了7条不同的错误路径。与尝试随机回溯相比,有一个启发性的方法总是一个好主意。比如,在这种情况下,我们知道下一步可能是在南部或东部方向,那么检查第一步的路径是更好的策略。
请注意,回溯并不是骑士巡演问题的最佳解决方案。有关其他更好的解决方案,请参阅下面的文章。这篇文章的目的是用一个例子来解释回溯。 求解骑士巡游问题的Warnsdorff算法
参考资料: http://see.stanford.edu/materials/icspacs106b/H19-RecBacktrackExamples.pdf http://www.cis.upenn.edu/~matuszek/cit594-2009/notices/35回溯。幻灯片演示文件 http://mathworld.wolfram.com/KnightsTour.html http://en.wikipedia.org/wiki/Knight%27s_tour 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



