数据结构和算法|集22

在2005门CS考试中提出了以下问题。

1） 程序P读取[0..100]范围内的500个整数，代表500名学生的分数。然后，它会打印每个分数高于50的频率。P存储频率的最佳方式是什么？ （a） 由50个数字组成的数组 （b） 100个数字的数组 （c） 500个数字的数组 （d） 由550个数字组成的动态分配数组

答复（a） 大小为50的数组看起来是存储每个分数的学生人数的最佳选择。我们需要存储分数高于50的频率。我们可以忽略低于50分的分数，而要对高于50分的分数进行索引，我们可以从分数值中减去50分/

2） 无向图G有n个节点。它的邻接矩阵由一个n×n平方矩阵给出，其（i）对角元素为0，且（ii）非对角元素为1。以下哪一项是真的？ （a） 图G没有最小生成树（MST） （b） 图G具有唯一的成本MST n-1 （c） 图G有多个不同的MST，每个成本为n-1 （d） 图G有多个不同代价的生成树

答复（c） 如果所有非对角元素均为1，则每个顶点都与图中的其他顶点连接，且边的权重为1。这样的图有多个成本为n-1的不同MST。请参见下面的示例。

连通图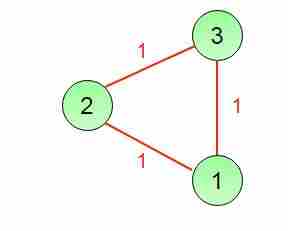： 下面是三个最小生成树，每个树的成本为2.0。 最小生成树1

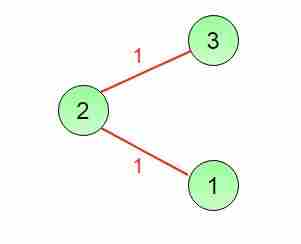最小生成树2

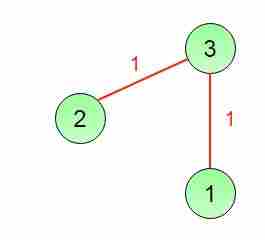最小生成树3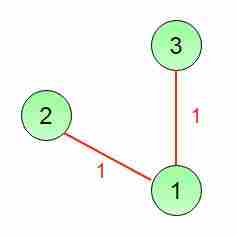

3） 已知在一组n个元素上计算二元关系的传递闭包的时间复杂度为： a） O（n） b） O（nLogn） c） O（n^（3/2）） d） O（n^3）

答复（d） 在数学中，集合X上二元关系R的传递闭包是X上包含R的最小传递关系。如果原始关系是传递的，传递闭包将是相同的关系；否则，传递闭包将是一个不同的关系。

在计算机科学中，传递闭包的概念可以被认为是构造了一个数据结构，使得回答可达性问题成为可能。也就是说，一个人能否在一个或多个跳中从节点a到达另一个节点b？二元关系只告诉您节点A连接到节点b，节点b连接到节点c，等等。在O（1）操作中构造传递闭包后，可以确定节点c可以从节点A到达。

沃沙尔算法 可以用来构造有向图的传递闭包（）。在Warshall最初的算法公式中，图是未加权的，由布尔邻接矩阵表示。然后将加法运算替换为逻辑合取（AND），将最小运算替换为逻辑析取（OR）。

参考资料： http://en.wikipedia.org/wiki/Floyd%E2%80%93Warshall_algorithm http://en.wikipedia.org/wiki/Transitive_closure

4.优先级队列被实现为最大堆。最初，它有5个元素。堆的级别顺序遍历如下所示： 10, 8, 5, 3, 2 两个新元素“1”和“7”按顺序插入堆中。插入元素后，堆的级别顺序遍历为： （a） 10,8,7,5,3,2,1 （b） 10,8,7,2,3,1,5 （c） 10,8,7,1,2,3,5 （d） 10,8,7,3,2,1,5

答复（D）

原始最大堆是：

        10
       /  
      8    5
     / 
    3   2

在插入1之后。

         10
       /    
      8      5
     /     /
    3   2 1 

插入7之后。

         10
       /   
      8     7
    /     /  
   3   2  1   5

请看 门角 所有上一年的论文/解决方案/解释、教学大纲、重要日期、笔记等。

如果您发现任何答案/解释不正确，或者您想分享有关上述主题的更多信息，请发表评论。