这个 泊松过程 是概率论中最重要、应用最广泛的过程之一。它被广泛用于建模时间或空间上的随机点。在本文中,我们将简要讨论齐次泊松过程。
泊松过程—— 这里我们将泊松过程作为一个计数过程来推导。假设我们正在观察特定时间段内特定事件的发生次数。(这里我们考虑时间作为一个例子,我们也可以考虑空间等),我们可以认为它们是在泊松过程中发生的,只要它们满足下面的条件。
- 在不相交的时间间隔内发生的次数是独立的。
- 在一个小的时间间隔内发生单一事件的概率与时间间隔的长度成正比。
- 在一个小的时间间隔内发生多次的概率可以忽略不计。
如果我们将长度为t的时间间隔内发生的次数表示为X(t),那么 ![]()
示例—— 许多现实生活中的情况可以用泊松过程建模。假设我们考虑了道路交通事故的数量。我们很容易理解,上述三个条件都得到了满足。由于两个不相交的时间间隔,给定道路上的事故数量是独立的,同样,在很短的时间间隔内发生两起或两起以上事故的可能性也很小。直观地说,我们也可以假设,在一个小的时间间隔内发生事故的概率与时间间隔的长度成正比。一个地方的地震数量也可以用泊松过程来模拟。
推导- 现在我们证明了我们的主张,如果X(t)是长度为t的区间内出现的次数,那么 ![]() 哪里
哪里 ![]() 是发生率。
是发生率。
我们将用数学归纳法来证明这个说法。首先,我们用数学术语写出上面的假设。根据假设3,在小时间间隔h内 ![]() 哪里
哪里 ![]() 当h趋于0或
当h趋于0或 ![]() . 再来一次如果
. 再来一次如果 ![]() 是发生率,根据假设2我们得到,
是发生率,根据假设2我们得到, ![]() .
.
我们取一个区间(0,t)和一个小区间(t,t+h)。我们将P(X(t)=n)表示为 ![]() .所以上面的方程可以写成:,
.所以上面的方程可以写成:, ![]() 或
或 ![]()
所以我们必须证明这一点 ![]() . 首先,我们将证明n=0和n=1的结果。然后我们将证明,如果n=m的结果为真,那么n=m+1的结果为真。
. 首先,我们将证明n=0和n=1的结果。然后我们将证明,如果n=m的结果为真,那么n=m+1的结果为真。
取时间间隔(0,t+h)。现在 ![]() (因为间隔(0,t)和(t,t+h)中的事件是独立的)或,
(因为间隔(0,t)和(t,t+h)中的事件是独立的)或, ![]() 或
或 ![]() .
.
当h趋于零时,我们得到极限, ![]() . 上述微分方程的解是,
. 上述微分方程的解是, ![]() , 以初始条件为例
, 以初始条件为例 ![]() 我们计算c=0。因此
我们计算c=0。因此 ![]() ,所以我们的说法对n=0是正确的。
,所以我们的说法对n=0是正确的。
现在我们试着证明n=1。 ![]() (我们使用的事实是,事件必须在区间(0,t)和(t,t+h)中的任何一个)内发生,或者
(我们使用的事实是,事件必须在区间(0,t)和(t,t+h)中的任何一个)内发生,或者 ![]() , 或
, 或 ![]() .
.
当h趋于零时,再次取极限, ![]() . 这是一阶线性微分方程,解是,
. 这是一阶线性微分方程,解是, ![]() 哪里
哪里 ![]() 这是一个常数。自从
这是一个常数。自从 ![]() .我们得到,
.我们得到, ![]() 因此
因此 ![]() 或
或 ![]() . 所以我们的说法对n=1是正确的。我们假设我们的说法对n=m是正确的。
. 所以我们的说法对n=1是正确的。我们假设我们的说法对n=m是正确的。
我们将证明这对于n=m+1是正确的。所以 ![]() , (我们假设m+1事件可以以不同的方式发生,例如(0,t)中的m+1事件和(t,t+h)中的无事件,或者(0,t)和1中的m事件。在(t,t+h)中出现,或在(0,t)中出现m-j,在(t,t+h)中出现j+1,j=1到m)。所以
, (我们假设m+1事件可以以不同的方式发生,例如(0,t)中的m+1事件和(t,t+h)中的无事件,或者(0,t)和1中的m事件。在(t,t+h)中出现,或在(0,t)中出现m-j,在(t,t+h)中出现j+1,j=1到m)。所以 ![]() 自从
自从 ![]() 对于j>=1。 或
对于j>=1。 或 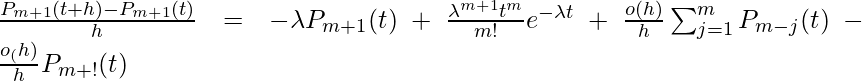
当h为零时取极限, ![]() . 这也是一阶微分方程,它的解是,
. 这也是一阶微分方程,它的解是, ![]() . 如果我们假设
. 如果我们假设 ![]() 我们得到
我们得到 ![]() .
.
所以最终的结果是, ![]() . 从而证明了这一结果。
. 从而证明了这一结果。
因此,我们导出了泊松过程中出现次数的pmf,这是一个带参数的泊松分布 ![]() .现在如果这个
.现在如果这个 ![]() 是时间的函数,我们称之为 非齐次泊松过程 .
是时间的函数,我们称之为 非齐次泊松过程 .
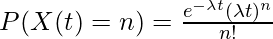


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



