给定一个正整数数组(可能包含 复制品 ),任务是找到其乘积等于给定数字的三胞胎数 T .
null
例子 :
Input: arr = [1, 31, 3, 1, 93, 3, 31, 1, 93] t = 93Output: 18Input: arr = [4, 2, 4, 2, 3, 1] t = 8Output: 4 [(4, 2, 1), (4, 2, 1), (2, 4, 1), (4, 2, 1)]
天真的方法: 解决这个问题的最简单方法是将每个可能的三元组与 T 如果它们的乘积等于 T .
以下是上述方法的实施情况:
C++
// C++ program for above implementation #include<iostream> using namespace std ; int main() { // The target value for which // we have to find the solution int target = 93 ; int arr[] = {1, 31, 3, 1, 93, 3, 31, 1, 93}; int length = sizeof (arr) / sizeof (arr[0]) ; // This variable contains the total // count of triplets found int totalCount = 0 ; // Loop from the first to the third //last integer in the list for ( int i = 0 ; i < length - 2; i++) { // Check if arr[i] is a factor // of target or not. If not, // skip to the next element if (target % arr[i] == 0) { for ( int j = i + 1 ; j < length - 1; j++) { // Check if the pair (arr[i], arr[j]) // can be a part of triplet whose // product is equal to the target if (target % (arr[i] * arr[j]) == 0) { // Find the remaining // element of the triplet int toFind = target / (arr[i] * arr[j]) ; for ( int k = j + 1 ; k < length ; k++ ) { // If element is found. increment // the total count of the triplets if (arr[k] == toFind) { totalCount ++ ; } } } } } } cout << "Total number of triplets found : " << totalCount ; return 0 ; } // This code is contributed by ANKITRAI1 |
JAVA
// Java program for above implementation class GFG { public static void main(String[] args) { // The target value for which // we have to find the solution int target = 93 ; int [] arr = { 1 , 31 , 3 , 1 , 93 , 3 , 31 , 1 , 93 }; int length = arr.length; // This variable contains the total // count of triplets found int totalCount = 0 ; // Loop from the first to the third //last integer in the list for ( int i = 0 ; i < length - 2 ; i++) { // Check if arr[i] is a factor // of target or not. If not, // skip to the next element if (target % arr[i] == 0 ) { for ( int j = i + 1 ; j < length - 1 ; j++) { // Check if the pair (arr[i], arr[j]) // can be a part of triplet whose // product is equal to the target if (target % (arr[i] * arr[j]) == 0 ) { // Find the remaining // element of the triplet int toFind = target / (arr[i] * arr[j]); for ( int k = j + 1 ; k < length ; k++ ) { // If element is found. increment // the total count of the triplets if (arr[k] == toFind) { totalCount ++ ; } } } } } } System.out.println( "Total number of triplets found : " + totalCount); } } // This code is contributed by mits |
Python3
# Python program for above implementation # The target value for which we have # to find the solution target = 93 arr = [ 1 , 31 , 3 , 1 , 93 , 3 , 31 , 1 , 93 ] length = len (arr) # This variable contains the total # count of triplets found totalCount = 0 # Loop from the first to the third # last integer in the list for i in range (length - 2 ): # Check if arr[i] is a factor of target # or not. If not, skip to the next element if target % arr[i] = = 0 : for j in range (i + 1 , length - 1 ): # Check if the pair (arr[i], arr[j]) can be # a part of triplet whose product is equal # to the target if target % (arr[i] * arr[j]) = = 0 : # Find the remaining element of the triplet toFind = target / / (arr[i] * arr[j]) for k in range (j + 1 , length): # If element is found. increment the # total count of the triplets if arr[k] = = toFind: totalCount + = 1 print ( 'Total number of triplets found: ' , totalCount) |
C#
// C# program for above implementation using System; class GFG { public static void Main() { // The target value for which // we have to find the solution int target = 93 ; int [] arr = {1, 31, 3, 1, 93, 3, 31, 1, 93}; int length = arr.Length; // This variable contains the total // count of triplets found int totalCount = 0 ; // Loop from the first to the third //last integer in the list for ( int i = 0 ; i < length - 2; i++) { // Check if arr[i] is a factor // of target or not. If not, // skip to the next element if (target % arr[i] == 0) { for ( int j = i + 1 ; j < length - 1; j++) { // Check if the pair (arr[i], arr[j]) // can be a part of triplet whose // product is equal to the target if (target % (arr[i] * arr[j]) == 0) { // Find the remaining // element of the triplet int toFind = target / (arr[i] * arr[j]); for ( int k = j + 1 ; k < length ; k++ ) { // If element is found. increment // the total count of the triplets if (arr[k] == toFind) { totalCount ++ ; } } } } } } Console.Write( "Total number of triplets found : " + totalCount); } } |
PHP
<?php // PHP program for above implementation // The target value for which // we have to find the solution $target = 93 ; $arr = array (1, 31, 3, 1, 93, 3, 31, 1, 93); $length = sizeof( $arr ); // This variable contains the // total count of triplets found $totalCount = 0 ; // Loop from the first to the // third last integer in the list for ( $i = 0 ; $i < $length - 2; $i ++) { // Check if arr[i] is a factor // of target or not. If not, // skip to the next element if ( $target % $arr [ $i ] == 0) { for ( $j = $i + 1 ; $j < $length - 1; $j ++) { // Check if the pair (arr[i], arr[j]) // can be a part of triplet whose // product is equal to the target if ( $target % ( $arr [ $i ] * $arr [ $j ]) == 0) { // Find the remaining // element of the triplet $toFind = $target / ( $arr [ $i ] * $arr [ $j ]) ; for ( $k = $j + 1 ; $k < $length ; $k ++ ) { // If element is found. increment // the total count of the triplets if ( $arr [ $k ] == $toFind ) { $totalCount ++ ; } } } } } } echo ( "Total number of triplets found : " ); echo ( $totalCount ); // This code is contributed // by Shivi_Aggarwal ?> |
Javascript
<script> // Javascript program for above implementation // The target value for which // we have to find the solution var target = 93; var arr = [ 1, 31, 3, 1, 93, 3, 31, 1, 93 ]; var length = arr.length; // This variable contains the total // count of triplets found var totalCount = 0; // Loop from the first to the third // last integer in the list for ( var i = 0; i < length - 2; i++) { // Check if arr[i] is a factor // of target or not. If not, // skip to the next element if (target % arr[i] == 0) { for ( var j = i + 1; j < length - 1; j++) { // Check if the pair (arr[i], arr[j]) // can be a part of triplet whose // product is equal to the target if (target % (arr[i] * arr[j]) == 0) { // Find the remaining // element of the triplet var toFind = target / (arr[i] * arr[j]); for ( var k = j + 1; k < length; k++) { // If element is found. increment // the total count of the triplets if (arr[k] == toFind) { totalCount ++; } } } } } } document.write( "Total number of triplets found : " + totalCount); // This code is contributed by rutvik_56 </script> |
输出:
Total number of triplets found: 18
时间复杂性: O( ![]() )
)
有效方法:
- 去掉那些不是因素的数字 T 从阵列中。
- 然后对数组进行排序,这样我们就不必验证每个数字的索引,从而避免额外的成对计数。
- 然后将每个数字出现在字典中的次数存储起来 计数 .
- 使用两个循环,通过检查其乘积是否相除,找到有效三元组的前两个数字 T
- 找到三元组的第三个数字,检查我们是否已经看到了三元组,以避免重复计算
- 计算该三元组的所有可能组合,使它们以相同的顺序出现(所有对都应遵循顺序(x、y、z),以避免重复)
JAVA
// java program for the above approach import java.io.*; import java.lang.*; import java.util.*; class GFG { // This function returns the total number of // combinations of the triplet (x, y, z) possible in the // given list static int Combinations( int x, int y, int z, HashMap<Integer, Integer> count) { int valx = count.getOrDefault(x, 0 ); int valy = count.getOrDefault(y, 0 ); int valz = count.getOrDefault(z, 0 ); if (x == y) { if (y == z) { return (valx * (valy - 1 ) * (valz - 2 )) / 6 ; } else { return ((((valy - 1 ) * valx) / 2 ) * valz); } } else if (y == z) { return valx * (((valz - 1 ) * valy) / 2 ); } else { return (valx * valy * valz); } } // Driver code public static void main(String[] args) { // Value for which solution has to be found int target = 93 ; int ar[] = { 1 , 31 , 3 , 1 , 93 , 3 , 31 , 1 , 93 }; // length of the array int N = ar.length; // Create a list of integers from arr which // contains only factors of the target // Using list comprehension ArrayList<Integer> list = new ArrayList<>(); for ( int i = 0 ; i < N; i++) if (ar[i] != 0 && target % ar[i] == 0 ) list.add(ar[i]); // Sort the list Collections.sort(list); int length = list.size(); // ArrayList to Array Conversion int [] arr = list.stream().mapToInt(i -> i).toArray(); // Initialize the Map with the default value HashMap<Integer, Integer> count = new HashMap<>(); HashSet<String> tripletSeen = new HashSet<>(); // Count the number of times a value is present in // the list and store it in a Map for further // use for ( int val : list) count.put(val, count.getOrDefault(val, 0 ) + 1 ); // Used to store the total number of triplets int totalCount = 0 ; for ( int i = 0 ; i < length - 2 ; i++) { for ( int j = i + 1 ; j < length - 1 ; j++) { // Check if the pair (arr[i], arr[j]) can be // a part of triplet whose product is equal // to the target if (target % (arr[i] * arr[j]) == 0 ) { int toFind = target / (arr[i] * arr[j]); // This condition makes sure that a // solution is not repeated int a[] = { arr[i], arr[j], toFind }; Arrays.sort(a); String str = (a[ 0 ] + "#" + a[ 1 ] + "#" + a[ 2 ]); if (toFind >= arr[i] && toFind >= arr[j] && tripletSeen.contains(str) == false ) { tripletSeen.add(str); totalCount += Combinations( arr[i], arr[j], toFind, count); } } } } System.out.println( "Total number of triplets found: " + totalCount); } } // This code is contributed by Kingash. |
Python3
# Python3 code to find the number of triplets # whose product is equal to a given number # in quadratic time # This function is used to initialize # a dictionary with a default value from collections import defaultdict # Value for which solution has to be found target = 93 arr = [ 1 , 31 , 3 , 1 , 93 , 3 , 31 , 1 , 93 ] # Create a list of integers from arr which # contains only factors of the target # Using list comprehension arr = [x for x in arr if x ! = 0 and target % x = = 0 ] # Sort the list arr.sort() length = len (arr) # Initialize the dictionary with the default value tripletSeen = defaultdict( lambda : False ) count = defaultdict( lambda : 0 ) # Count the number of times a value is present in # the list and store it in a dictionary for further use for key in arr: count[key] + = 1 # Used to store the total number of triplets totalCount = 0 # This function returns the total number of combinations # of the triplet (x, y, z) possible in the given list def Combinations(x, y, z): if x = = y: if y = = z: return (count[x] * (count[y] - 1 ) * (count[z] - 2 )) / / 6 else : return ((((count[y] - 1 ) * count[x]) / / 2 ) * count[z]) elif y = = z: return count[x] * (((count[z] - 1 ) * count[y]) / / 2 ) else : return (count[x] * count[y] * count[z]) for i in range (length - 2 ): for j in range (i + 1 , length - 1 ): # Check if the pair (arr[i], arr[j]) can be a # part of triplet whose product is equal to the target if target % (arr[i] * arr[j]) = = 0 : toFind = target / / (arr[i] * arr[j]) # This condition makes sure that a solution is not repeated if (toFind > = arr[i] and toFind > = arr[j] and tripletSeen[(arr[i], arr[j], toFind)] = = False ): tripletSeen[(arr[i], arr[j], toFind)] = True totalCount + = Combinations(arr[i], arr[j], toFind) print ( 'Total number of triplets found: ' , totalCount) |
输出:
Total number of triplets found: 18
时间复杂性: O( ![]() )
)
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END
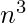


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



