给定周长P,任务是找到周长等于P的可能直角三角形的数量。 例如:
null
Input: P = 12Output: number of right triangles = 1 The only right angle possible is with sides hypotenuse = 5, perpendicular = 4 and base = 3. Input: p = 840Output: number of right triangles = 8
目的是求出满足方程a+b+c=p和a的解的个数 2. +b 2. =c 2. . A. 缺乏经验的 方法是为a(1到p/2)和b(a+1到p/3)运行两个循环,然后使c=p-a-b,如果需要,则增加一个计数 ![]() .这需要
.这需要 ![]() 时间 一 有效率的 方法可以通过少量代数操作找到:
时间 一 有效率的 方法可以通过少量代数操作找到:
因为a+c>b或,p-b>b或,b
毕达哥拉斯定理 .使用配对列表存储带的值,并在末尾返回计数。 以下是上述方法的实施情况。
C++
// C++ program to find the number of // right triangles with given perimeter #include<bits/stdc++.h> using namespace std; // Function to return the count int countTriangles( int p) { // making a list to store (a, b) pairs vector<pair< int , int >> store; // no triangle if p is odd if (p % 2 != 0) return 0; else { int count = 1; for ( int b = 1; b < p / 2; b++) { float a = ( float )p / 2.0f * (( float )(( float )p - 2.0 * ( float )b) / (( float )p - ( float )b)); int inta = ( int )(a); if (a == inta) { // make (a, b) pair in sorted order pair< int , int > ab; if (inta<b) { ab = {inta, b}; } else { ab = {b, inta}; } // check to avoid duplicates if (find(store.begin(), store.end(), ab) == store.end()) { count += 1; // store the new pair store.push_back(ab); } } } return count; } } // Driver Code int main() { int p = 840; cout << "number of right triangles = " << countTriangles(p); return 0; } // This code is contributed by rutvik_56. |
JAVA
// Java program to find the number of // right triangles with given perimeter import java.util.*; class GFG{ static class pair { int first, second; public pair( int first, int second) { this .first = first; this .second = second; } } // Function to return the count static int countTriangles( int p) { // making a list to store (a, b) pairs HashSet<pair> store = new HashSet<pair>(); // no triangle if p is odd if (p % 2 != 0 ) return 0 ; else { int count = 1 ; for ( int b = 1 ; b < p / 3 ; b++) { float a = ( float )p / 2 .0f * (( float )(( float )p - 2.0 * ( float )b) / (( float )p - ( float )b)); int inta = ( int )(a); if (a == inta) { // make (a, b) pair in sorted order pair ab; if (inta<b) { ab = new pair(inta, b); } else { ab = new pair(b, inta); } // check to astatic void duplicates if (!store.contains(ab) ) { count += 1 ; // store the new pair store.add(ab); } } } return count; } } // Driver Code public static void main(String[] args) { int p = 840 ; System.out.print( "number of right triangles = " + countTriangles(p)); } } // This code is contributed by Rajput-Ji |
Python3
# python program to find the number of # right triangles with given perimeter # Function to return the count def countTriangles(p): # making a list to store (a, b) pairs store = [] # no triangle if p is odd if p % 2 ! = 0 : return 0 else : count = 0 for b in range ( 1 , p / / 2 ): a = p / 2 * ((p - 2 * b) / (p - b)) inta = int (a) if (a = = inta ): # make (a, b) pair in sorted order ab = tuple ( sorted ((inta, b))) # check to avoid duplicates if ab not in store : count + = 1 # store the new pair store.append(ab) return count # Driver Code p = 840 print ( "number of right triangles = " + str (countTriangles(p))) |
C#
// C# program to find the number of // right triangles with given perimeter using System; using System.Collections.Generic; public class GFG { public class pair { public int first, second; public pair( int first, int second) { this .first = first; this .second = second; } } // Function to return the count static int countTriangles( int p) { // making a list to store (a, b) pairs HashSet<pair> store = new HashSet<pair>(); // no triangle if p is odd if (p % 2 != 0) return 0; else { int count = 1; for ( int b = 1; b < p / 3; b++) { float a = ( float ) p / 3 * (( float ) (( float ) p - 2 * ( float ) b) / (( float ) p - ( float ) b)); int inta = ( int ) (a); if (a == inta) { // make (a, b) pair in sorted order pair ab; if (inta < b) { ab = new pair(inta, b); } else { ab = new pair(b, inta); } // check to astatic void duplicates if (!store.Contains(ab)) { count += 1; // store the new pair store.Add(ab); } } } return count; } } // Driver Code public static void Main(String[] args) { int p = 840; Console.Write( "number of right triangles = " + countTriangles(p)); } } // This code is contributed by gauravrajput1 |
输出:
number of right triangles = 8
时间复杂性: O(P)
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


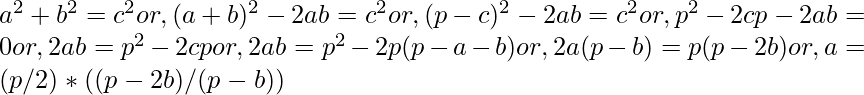

![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



