抽样理论

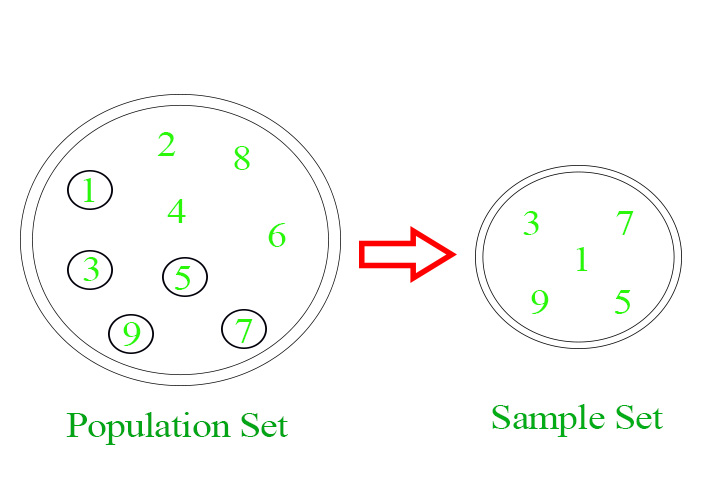
在统计学领域，在进行任何估计之前，首先要做的事情是从整个人口集中创建一个样本集。总体集可以被视为收集数据的整棵树，而样本集可以被视为对观测和估计进行实际研究的分支。种群树是一个非常大的集合，对其进行观测研究可能非常累人，无论是时间还是金钱方面。因此，为了减少时间和资源，从总体集创建一个样本集。

抽样过程 :

1. 确定人口集。
2. 我们样本量的确定。
3. 为从总体培养基中选择样本提供基础培养基。
4. 使用简单随机、系统或分层抽样等多种抽样技术中的一种从介质中挑选样本。
5. 检查形成的样本集是否包含与总体集的不同属性实际匹配的元素，两者之间没有很大差异。
6. 检查形成的样本集中是否存在错误或不准确的估计，这些错误或估计可能已经发生，也可能没有发生
7. 我们在执行上述步骤后得到的集合实际上构成了样本集。

这是一个简单的例子，说明如何在基本阶段进行采样。

人口

人口 是统计研究中考虑的一整套变量、元素和实体。它也被称为通用集，从中可以得出实际的推论。人口集由考虑中的个人或元素的所有属性组成，但对人口进行估计不仅会消耗资源，而且在时间上也是如此。

实例 想想地球上所有男人的平均体重。在这里，这被认为是一个假设的人口，因为它包括所有曾经在地球上生活过的人，其中包括将在未来生存的人，以及在我们之前生活过的人。但是，在进行这种测量时，出现了一种反常现象，即并非所有人口中的男性都是可以观察到的（考虑男性，他们将在未来存在，也考虑男性，他们曾经生活过，但现在不存在）。此外，对人口样本进行统计（如果假设可能的话）将需要大量的时间和资源，这也将是彻底和低效的。

因此，我们要做的是从可用人口中提取一个子集，对其进行统计，并对整个人口进行推断。取出一个子集，会使任务更容易，因为检查该子集所需的时间少于检查整个群体所需的时间。对样本集进行统计，得出关于整个人口的结论。计算被认为是总体集的结论，因为它不能用总体集的实际数据进行测量，也不能没有错误。这一点很明显，因为样本集用作中间框架，成员较少，因此会丢失一些信息。（这会导致错误）。

采样框

采样框是采样介质的基础。它是所有观察到的样本元素的集合。有时甚至可能发生抽样框架中的所有元素都没有参与实际统计。在这种情况下，参与研究的元素被称为 样品 以及可能参与研究但未参与研究的潜在元素 采样框。 因此，抽样框架是我们将执行统计的潜在元素列表。 提出一个好的抽样框架是非常必要的，因为它将有助于预测统计结果对总体集的反应。采样帧不仅仅是一组随机挑选的元素，它甚至还包括标识符，这些标识符有助于识别集合中的每个元素。

例子： Geeksforgeks在德里组织了一个由印度各地的极客实习生组成的会议，对他们的表现进行统计研究。GfG向所有500名实习生发送了一封邀请电子邮件，但由于所有实习生都分散在印度各地，200人中有500人实际参加了培训。因此，GfG只能对200名学生进行研究（样本集）。但剩下的300人可能是该研究中的潜在候选人，但决定不出现在抽样框架中。

抽样方法和类型 :

1. 简单随机抽样
2. 系统抽样
3. 分层抽样

这些是使用最广泛的采样过程，每种都有其优点和缺点。

让我们详细了解每种采样方法：

1. 简单随机抽样 ：简单随机抽样是最基本的抽样形式。在该方法中，首先将总体中的所有元素划分为大小相等的随机集。随机集之间没有定义属性，即不能基于某些特定标识符从另一个集合中识别一个集合。因此，每个元素都具有相同的被选择属性。 P（被选中的可能性）=

   使用SRS的基本方法有：

   • 选择人口集
   • 确定抽样的依据
   • 使用随机数/会话生成器从每组中选取一个元素。
   

   简单随机抽样

   赞成的意见：

   • 由于时间是最基本的抽样形式，因此对时间的要求不那么详尽
   • 对于元素数量非常少的总体集非常有用
   • SRS可以在任何地方、任何时间使用，甚至不需要使用特殊的随机发生器

   欺骗：

   • 对于大的人口集来说是无效的
   • 在上述三种抽样方法中，造成错误最多的是
   • 存在偏差的可能性，然后SRS将无法提供正确的结果
   • 不提供特定标识符来分离统计上相似的样本
2. 系统抽样 ：系统抽样也称为一种概率抽样。它比SRS精确得多，而且标准误差形成百分比非常低，但并非无误差。在这种方法中，首先，根据特定的顺序或方案（通常称为“正在排序”）排列填充托盘元素。它可以是任何顺序，这完全取决于执行统计的人员。元素首先按升序、降序、词典或测试人员认为合适的任何其他已知方法排列。虽然每次的起点都需要是随机的。排列后，根据预定义的间隔集或函数拾取样本元素。 实例 ：在一组元素范围为1到100的随机数字中。元素首先按升序或降序排序。然后假设每4个元素都被选为采样帧的一部分。这种抽样被称为系统抽样。

   P（被选中的概率）=[取决于排序后的有序填充托盘]

   采用系统随机抽样的基本方法是：-

   • 明智地选择人群
   • 检查系统抽样是否是有效的方法。
   • 如果是，则应用排序方法获得一对有序的总体元素。
   • 选择一个周期来提取元素。
   

   系统抽样法

   赞成的意见：

   • 精度高于SRS。
   • 标准错误概率较小。
   • 在创建样本框架的过程中，不会出现偏移。

   欺骗：

   • 在时间方面效率不高
   • 人口元素的周期性会导致荒谬的结果。
   • 系统抽样可以提供最准确的结果，也可以提供不可能的结果。
3. 分层抽样 ：分层抽样是上述三种抽样方法中最复杂的一种。它是一种既涉及简单随机抽样又涉及系统抽样的混合方法。它是最先进的采样方法之一，为测试人员提供近乎准确的结果。在这种方法中，人口托盘被划分为子段，也称为地层（单数）。每个阶层都有自己独特的财产。在划分成不同的子层后，SRS或系统抽样可用于创建和挑选样本进行统计。 分层抽样的基本方法有：
   • 明智地选择人口。
   • 检查周期性或任何其他特征，以便将其划分为不同的地层
   • 根据选择性质将种群划分为子集和分组。
   • 使用SRS或对每个地层进行系统采样，形成样本框架。
   • 我们甚至可以对不同的子集应用不同的采样方法。
   

   分层抽样的视觉表现。

   赞成的意见：

   • 提供高精度测量结果。
   • 只要改变取样方法，就可以得到不同的结果。
   • 该方法还可以在抽取样本时比较不同的地层。

   欺骗：

   • 在资源和资金方面效率低下且成本高昂。
   • 这种方法只有在存在元素同质性的罕见情况下才会失败。

这三种是目前广泛使用的抽样方法。它们各有优缺点。因此，必须明智地选择抽样方法，因为错误的选择可能会导致错误的答案。