TCS安置论文| MCQ 1-yiteyi-C++库

这是一份用于能力倾向准备的TCS模型放置论文。本学位论文将涵盖TCS招聘活动中提出的能力倾向问题，并严格遵循TCS面试中提出的问题模式。建议您解决以下每一个问题，以增加您通过TCS面试的机会。

null

进行了一次检查，并对以下内容进行了分析。4名男性能够在8天内定期检查一些试卷，工作时间为5小时。两个人在20天内检查试卷数量翻倍所需的总小时数是多少？
```
Answer: 8 hours
```
解决方案：

假设1个单位的工作在1小时内完成让我们计算总工作时间： =>4*8*5=160个单位现在工作翻了一番： =>160*2=320个单位 x是两个人在20天内完成工作所需的小时数。因此 =>2*20*x=320 =>x=8小时（答案）。
从101到150的数字写为101102103104105…146147148149150。当总数除以3时，余数是多少？
```
Answer: 2
```
解决方案：

3的可分性规则是一个数字的所有数字之和都应该可以被3整除。让我们计算数字之和：有50个1（单位位置）=50 有10个1（十位）=10 有10个2（十位）=20 有10个3（十位）=30 有10个4（十位）=40 有一个5（十位数）=5 对于每个数字1到9，有5组和45（1+2+…+9）=225 =>所有数字之和=380 =>380/3=2（答案）
如果字母表是按a、bb、ccc、dddd、eeeee、ffffff……的顺序书写的…。第120个字母是什么？
```
Answer: O
```
解决方案：

可以看出，字母是按AP顺序排列的，所以应用我们得到的公式， $n(n+1)/2 <= 120$ 我们发现n=15符合这个方程英语字母表中的第15个字母=O 所以第15项包含O。
有一个油箱的1/7部分充满了燃料。如果向油箱中倒入22升燃油，指示灯将升至油箱的1/5标记。那么油箱的总容量是多少？
```
Answer: 385
```
解决方案：

让油箱的总容量为“x”升。根据问题， =>x/7+22=x/5 =>x/5–x/7=22 =>x=385升（答案）
有多少素数介于3和100之间（不包括值），满足以下条件：
```
Answer: 2
```
解决方案：

3到100之间有23个素数（不包括值），它们都是奇数。 5y–1为奇数，5y必须为偶数对于5y来说是相等的y应该是相等的。以y为2，我们得到5y–1为9。现在看看那些以9=9，19，29，39，59，79，89结尾的素数其中，满足两个方程（假定为整数）的数字分别为9、29和89。我们不能考虑9，因为它违反了数字的约束应该大于3。所以答案是2（29和89）
在给定的图中，求出正方形面积与三角形面积之比： a） 3:2 b） 2:3 c） 2:1 d） 1:2
```
Answer: c) 2:1
```
解决方案：

让正方形的侧面为“2”个单位正方形的面积=（边）^2= 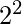$2^2$ =4个单位三角形的边，使用毕达哥拉斯定理= 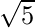$sqrt{5}$ 单元三角形的高度=正方形的边（使用毕达哥拉斯定理）三角形面积=1/2*底部*高度这里，底部=高度=侧面三角形面积=1/2*（边）^2 => 1/2 *2 * 2 =>2台因此，比率=4:2 =>2:1（答案）
有一个仙女岛，岛上住着一个骑士、一个无赖和一个间谍。你去那里遇到三个人，假设是A、B和C，其中一个是骑士，一个是无赖，一个是间谍。众所周知，骑士总是说真话，无赖总是撒谎，间谍要么撒谎，要么说真话。
那么谁是骑士，谁是无赖，谁是间谍？
```
Answer: A = Knight, B = Spy, C = Knave
```
解决方案：

假设A是骑士，然后他说的是真话，C是撒谎的无赖，最后B是无赖，他说的是关于A的真话。所以这个条件成立。假设B是骑士。然后它与答案相矛盾，因为一个骑士总是说真话，不可能有两个骑士。 C也是如此。
找出给定序列2013、2020、2027中的完美正方形数……………。，2300? （提示44^2=1936） a）二, b）一, c）三, d）以上都没有
```
Answer: b) 1
```
解决方案：

我们可以看到，这个系列是以AP的形式出现的，其公差为7。所以这个系列的形式是2013+7d 提示实际上是一种快捷方式： 44^2 = 1936 45^2 = 2025 46^2 = 2116 47^2 = 2209 48^2 = 2304 因此，在这些数字中，我们需要找出哪一个是以2013+7d的形式出现的表格2013+7*28中只能写一个数字2209。因此答案是1。
在7^1+7^2+7^3+7^4的系列中+7^204+7^205，单位位置为3的数字有多少？
```
Answer: 51
```
解决方案：根据7的周期性，单位数字遵循7、9、3、1的模式，并且重复。所以每4个数字中，我们就得到一个3。205除以4，我们得到51，这是下面问题的答案。
求1728的除数（包括1和数字本身）。
```
Answer: 28
```
解决方案：

这有一个直接公式：号码= 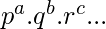$p^a.q^b.r^c...$ 其中p，q和r是素数。我们只需要对数字进行素数分解。然后，（a+1）。（b+1）。（c+1）是除数的数目。 1728年= 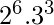$2^6.3^3$ 因此，（6+1）。(3+1) = 28

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章