顺序:
它是一组数字,按照一定的规则,以一定的顺序排列。 集合中的每一个数字都被称为序列中的一个项,其长度是序列中的项数。我们可以把序列写成 ![]() 有限序列通常由 1. A. 2. A. 3. …. A. N ,无限序列由 1. A. 2. A. 3. …. 无限远。序列{A N }有极限,我们写
有限序列通常由 1. A. 2. A. 3. …. A. N ,无限序列由 1. A. 2. A. 3. …. 无限远。序列{A N }有极限,我们写 ![]() 或
或 ![]() 像
像 ![]() . 例如:
. 例如:
2, 4, 6, 8 ...., 20 is a finite sequence obtained by adding 2 to the previous number. 10, 6, 2, -2, ..... is an infinite sequence obtained by subtracting 4 from the previous number.
如果一个序列的项可以用公式来描述,那么这个序列就叫做a 进展 .
1, 1, 2, 3, 5, 8, 13, ....., is a progression called the Fibonacci sequence in which each term is the sum of the previous two numbers.
定理:
定理1 :给定顺序 ![]() 如果我们有一个函数 f(x) 以至于 f(n) =
如果我们有一个函数 f(x) 以至于 f(n) = ![]() 和
和 ![]() 然后
然后 ![]() 这个定理基本上告诉我们,序列的极限,就像函数的极限一样。
这个定理基本上告诉我们,序列的极限,就像函数的极限一样。
定理2(挤压定理) :如果 ![]() 对于所有n>n对于某些n和
对于所有n>n对于某些n和 ![]() 然后
然后 ![]()
定理3 :如果 ![]() 然后
然后 ![]() . 注意,为了使这个定理成立,极限必须为零,对于极限不为零的序列,它不起作用。
. 注意,为了使这个定理成立,极限必须为零,对于极限不为零的序列,它不起作用。
定理4 :如果 ![]() 功能呢 F 持续的 L 然后
功能呢 F 持续的 L 然后 ![]()
定理5 :序列 ![]() 如果
如果 ![]() 对于 r的所有其他值。同样,
对于 r的所有其他值。同样, ![图片[18]-数学|序列、级数和求和-yiteyi-C++库](http://tutorial.math.lamar.edu/Classes/CalcII/Sequences_files/eq0069MP.gif) 这个定理是一个有用的定理,它给出了偶尔出现的序列的收敛/发散和值(当它收敛时)。
这个定理是一个有用的定理,它给出了偶尔出现的序列的收敛/发散和值(当它收敛时)。
属性:
如果 ![]() 和
和 ![]() 是收敛序列,具有以下特性:
是收敛序列,具有以下特性:
-
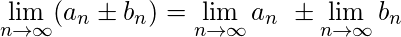
-
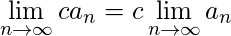
-
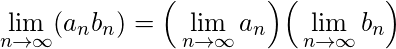
-
![Rendered by QuickLaTeX.com displaystylelim_{n oinfty} {a_n}^p = Big[displaystylelim_{n oinfty} a_nBig]^p](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a1c1b3c9f7ec2a1cbd26ceb17ca3a7ec_l3.png) 假如
假如 
最后一个属性是
![图片[26]-数学|序列、级数和求和-yiteyi-C++库](http://tutorial.math.lamar.edu/Classes/CalcII/Sequences_files/eq0052MP.gif)
系列:
级数就是序列中各个项的总和。 如果序列是
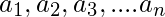 表情
表情 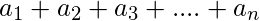 被称为与之相关的系列。系列由“S”或希腊符号表示
被称为与之相关的系列。系列由“S”或希腊符号表示 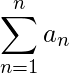 .级数可以是有限的,也可以是无限的。 例如:
.级数可以是有限的,也可以是无限的。 例如: 5 + 2 + (-1) + (-4) is a finite series obtained by subtracting 3 from the previous number. 1 + 1 + 2 + 3 + 5 is an infinite series called the Fibonacci series obtained from the Fibonacci sequence.
如果部分和序列是收敛序列(即其极限存在且有限),则该序列也被称为收敛序列 会聚性的 i、 e.如果
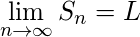 然后
然后 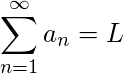 .同样,如果部分和序列是发散序列(即如果
.同样,如果部分和序列是发散序列(即如果 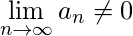 或者它的极限不存在,或者是正负无穷大),那么这个级数也叫做发散级数。
或者它的极限不存在,或者是正负无穷大),那么这个级数也叫做发散级数。 属性:
- 如果
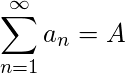 和
和 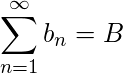 那么是收敛级数吗
那么是收敛级数吗 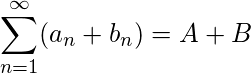
- 如果
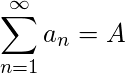 和
和 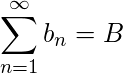 那么是收敛级数吗
那么是收敛级数吗 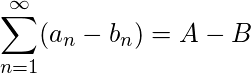
- 如果
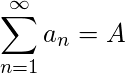 那么是收敛级数吗
那么是收敛级数吗 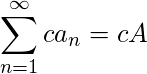
- 如果
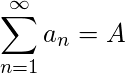 和
和 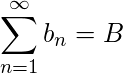 是收敛级数,如果
是收敛级数,如果 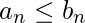 为了所有人
为了所有人 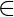 那么
那么 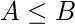
定理:
- 定理1(比较测试) : 认为
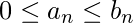 对于
对于 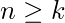 对一些k.那么 (1) 融合
对一些k.那么 (1) 融合 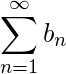 这意味着
这意味着 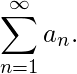 (2) 融合
(2) 融合 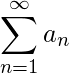 这意味着
这意味着 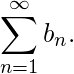
- 定理2(极限比较试验) : 允许
 和
和  ,假设
,假设 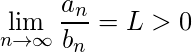 然后
然后 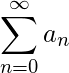 当且仅当
当且仅当 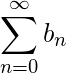 汇聚。
汇聚。
- 定理3(比率检验) : 假设存在以下限制:,
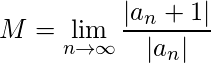 然后 (1) 如果
然后 (1) 如果 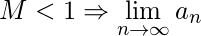 汇聚 (2) 如果
汇聚 (2) 如果 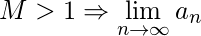 分歧 (3) 如果
分歧 (3) 如果 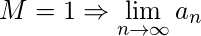 可能会趋同或分歧
可能会趋同或分歧
- 定理4(根检验) : 假设存在以下限制:,
![Rendered by QuickLaTeX.com M = displaystylelim_{n oinfty}sqrt[n]{|a_n|}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7ceb37eaac2861f1236afb4011125909_l3.png) 然后 (1) 如果
然后 (1) 如果 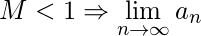 汇聚 (2) 如果
汇聚 (2) 如果 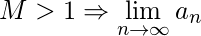 分歧 (3) 如果
分歧 (3) 如果 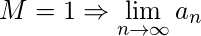 可能会趋同或分歧
可能会趋同或分歧
- 定理5(绝对收敛性检验) : 连续剧
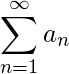 据说是 绝对收敛 如果这个系列
据说是 绝对收敛 如果这个系列 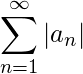 汇聚。
汇聚。
- 定理6(条件收敛性检验) : 连续剧
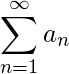 据说是 条件收敛 如果这个系列
据说是 条件收敛 如果这个系列 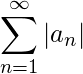 分歧,但系列
分歧,但系列 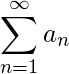 汇聚。
汇聚。
- 定理7(交替串联试验) : 如果
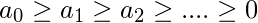 和
和 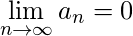 “交替系列”
“交替系列” 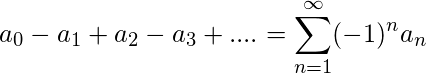 将汇聚。
将汇聚。
总结:
求和是一系列数字的相加。它是一种方便而简单的速记形式,用于给出变量值总和的简明表达式。 求和符号,
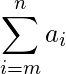 ,指示我们对序列中的元素求和。被求和序列的一个典型元素出现在求和符号的右侧。
,指示我们对序列中的元素求和。被求和序列的一个典型元素出现在求和符号的右侧。 属性:
-
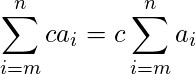 其中c是任意数。所以,我们可以从求和中求出常数。
其中c是任意数。所以,我们可以从求和中求出常数。
-
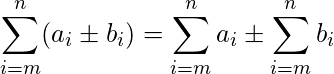 所以我们可以将求和分解为求和或求差。
所以我们可以将求和分解为求和或求差。
请注意,虽然我们可以像上面提到的那样分解总和和差值,但我们不能对产品和商做同样的事情。换句话说,
![图片[76]-数学|序列、级数和求和-yiteyi-C++库](http://tutorial.math.lamar.edu/Classes/CalcI/SummationNotation_files/eq0009M.gif)
-
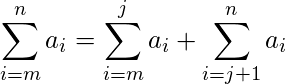 ,表示任何自然数
,表示任何自然数 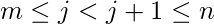 .
.
-
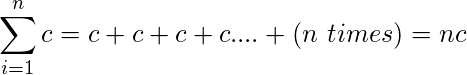 .如果求和的参数是常数,那么求和就是极限范围值乘以常数。
.如果求和的参数是常数,那么求和就是极限范围值乘以常数。
例如:
1) Sum of first n natural numbers:
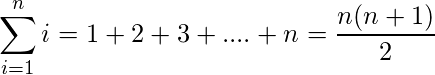 .
2) Sum of squares of first n natural numbers:
.
2) Sum of squares of first n natural numbers:
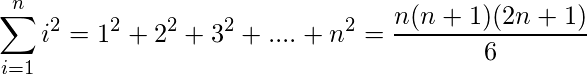 .
3) Sum of cubes of first n natural numbers:
.
3) Sum of cubes of first n natural numbers:
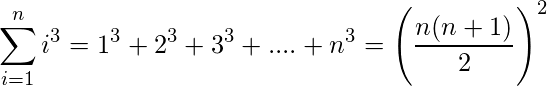 .
4) The property of logarithms:
.
4) The property of logarithms:
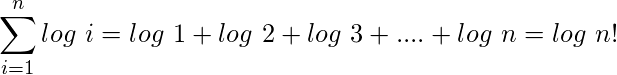 .
.
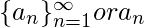


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



