自平衡二进制搜索树（比较）-yiteyi-C++库

自平衡二叉搜索树 是 高度平衡 二元搜索树，在树上执行插入和删除操作时，自动保持尽可能小的高度。高度通常保持在对数n的顺序，以便所有操作平均花费O（对数n）时间。

null

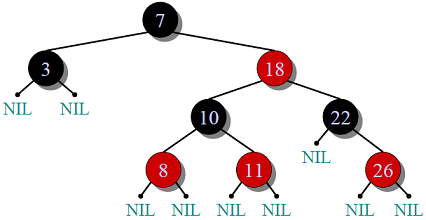
例如： 红黑树

Red Black Tree

AVL树：

图片[2]-自平衡二进制搜索树（比较）-yiteyi-C++库

语言实现： 设置和地图在C++ STL中。有序树和树图在爪哇。大多数库实现都使用红黑树。Python标准库不支持自平衡BST。在Python中，我们可以使用对分模块来保存一组已排序的数据。我们也可以使用PyPi模块，比如 rbtree （红黑树的实施）和皮亚维尔（AVL树的实现）。

自我平衡树如何保持高度？ 树木的一个典型操作是轮换。以下两个基本操作可以在不违反BST属性的情况下重新平衡BST（键（左） 1）左旋转 2）右旋

T1, T2 and T3 are subtrees of the tree rooted with y (on the left side) or x (on the right side)                y                               x    /      Right Rotation          /     x   T3   - - - - - - - >        T1   y   /        < - - - - - - -            /  T1  T2     Left Rotation            T2  T3Keys in both of the above trees follow the following order  keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)So BST property is not violated anywhere.

我们已经讨论过了平衡二叉树 , 红黑树和八字树 .在这篇文章中，我们将比较这些树的效率：

米制的	RB树	平衡二叉树	八字树
插入最坏情况	O（1）	O（logn）	摊销O（对数）
最大高度树的	*2log（n）**	*1.44对数（n）**	O（n）
搜索最坏的情况	O（logn），适度的	O（logn），更快	摊销O（对数），更慢的
高效的实施需要	每个节点带有颜色位的三个指针	两个指针，每个指针有一个平衡因子节点	只有两个指针没有额外信息
删除最坏的情况	O（logn）	O（logn）	摊销O（对数）
主要用于	作为通用数据结构	当需要频繁查找时	当相同的元素一次又一次
实际应用	数据库事务	多重集、多重映射、映射、集合等。	缓存实现、垃圾收集算法

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章