给定一个数字n,找到 第n位 居中十二面体数。 A. 中心十二面体数 是一类比喻数字。它由一个中心点构成,周围是连续的十二面体(12个平面的多面体)层。 前几个中心十二面体数 (其中n=0,1,2,3……) 是: 1, 33, 155, 427, 909, 1661 …………… 例如:
null
Input : 5Output : 1661Input :1Output :33
数学公式 N 居中十二面体数由下式给出:
以下是上述理念的基本实现:
C++
// Program to find nth centered // dodecahedral number #include <bits/stdc++.h> using namespace std; // Function to find // centered dodecahedral number int CenteredDodecahedral_num( long int n) { // Formula to calculate nth // centered dodecahedral number // and return it into main function. return (2 * n + 1) * (5 * n * n + 5 * n + 1); } // Driver Code int main() { long int n = 3; // print result cout << n << "th Centered Dodecahedral number : " ; cout << CenteredDodecahedral_num(n) << endl; n = 10; // print result cout << n << "th Centered Dodecahedral number : " ; cout << CenteredDodecahedral_num(n); return 0; } |
JAVA
// Java Program to find nth // centered dodecahedral number import java.io.*; class GFG { // Function to find centered // dodecahedral number static int CenteredDodecahedral_num( int n) { // Formula to calculate nth // centered dodecahedral number // and return it into main function. return ( 2 * n + 1 ) * ( 5 * n * n + 5 * n + 1 ); } // Driver Code public static void main (String[] args) { int n = 3 ; // print result System.out.print( n + "th Centered " + "Dodecahedral number : " ); System.out.println ( CenteredDodecahedral_num(n)); n = 10 ; // print result System.out.print( n + "th Centered " + "Dodecahedral number : " ); System.out.println( CenteredDodecahedral_num(n)); } } // This code is contributed by m_kit. |
Python3
# Program to find nth centered # dodecahedral number # Function to find centered # dodecahedral number def CenteredDodecahedral_num(n) : # Formula to calculate nth # centered dodecahedral number return ( 2 * n + 1 ) * ( 5 * n * n + 5 * n + 1 ) # Driver Code if __name__ = = '__main__' : n = 3 print (n, "rd centered dodecahedral number: " , CenteredDodecahedral_num(n)) n = 10 print (n, "th centered dodecahedral number : " , CenteredDodecahedral_num(n)) # This code is contributed by aj_36 |
C#
// C# Program to find // nth centered // dodecahedral number using System; class GFG { // Function to find // nth centered // dodecahedral number static int CenteredDodecahedral_num( int n) { // Formula to calculate // nth centered dodecahedral // number and return it // into main function. return (2 * n + 1) * (5 * n * n + 5 * n + 1); } // Driver Code static public void Main () { int n = 3; // print result Console.Write( n + "th Centered " + "Dodecahedral number : " ); Console.WriteLine( CenteredDodecahedral_num(n)); n = 10; // print result Console.Write( n + "th Centered " + "Dodecahedral number : " ); Console.WriteLine( CenteredDodecahedral_num(n)); } } // This code is contributed by ajit |
PHP
<?php // Program to find nth centered // dodecahedral number // Function to find // centered dodecahedral number function CenteredDodecahedral_num( $n ) { // Formula to calculate nth // centered dodecahedral number // and return it into main function. return (2 * $n + 1) * (5 * $n * $n + 5 * $n + 1); } // Driver Code $n = 3; // print result echo $n , "th Centered Dodecahedral " . "number : " ; echo CenteredDodecahedral_num( $n ), "" ; $n = 10; // print result echo $n , "th Centered Dodecahedral " . "number : " ; echo CenteredDodecahedral_num( $n ); // This code is contributed by akt_mit ?> |
Javascript
<script> // Javascript Program to find nth // centered dodecahedral number // Function to find centered // dodecahedral number function CenteredDodecahedral_num(n) { // Formula to calculate nth // centered dodecahedral number // and return it into main function. return (2 * n + 1) * (5 * n * n + 5 * n + 1); } // Driver code var n = 3; // print result document.write(n + "th Centered " + "Dodecahedral number : " ); document.write(CenteredDodecahedral_num(n) + "<br>" ); n = 10; // print result document.write(n + "th Centered " + "Dodecahedral number : " ); document.write(CenteredDodecahedral_num(n)); // This code is contributed by Khushboogoyal499 </script> |
输出:
3th Centered Dodecahedral number : 42710th Centered Dodecahedral number : 11571
时间复杂性: O(1) 辅助空间: O(1)
参考资料: https://en.wikipedia.org/wiki/Centered_dodecahedral_number
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END
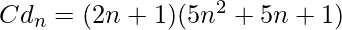


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



