在Euler巡更树中遍历的节点总数

309

树之旅 已经讨论了将树的层次结构展平为数组的方法，该数组包含 2*N-1 价值观在本文中，我们的任务是证明欧拉游程树的阶数是节点数减1的2倍。这里的度数是指在Euler Tour中遍历的节点总数。 例如：

null

输入：

图片[1]-在Euler巡更树中遍历的节点总数-yiteyi-C++库

产出：15 输入：

图片[2]-在Euler巡更树中遍历的节点总数-yiteyi-C++库

产出：17

说明： 使用 例1 :

图片[3]-在Euler巡更树中遍历的节点总数-yiteyi-C++库

哪里

图片[4]-在Euler巡更树中遍历的节点总数-yiteyi-C++库

可以看出，Euler Tour中每个节点的计数正好等于节点的出度加1。 从数学上讲，它可以表示为： $displaystyle Total=sum_{node_i=1}^{N} Out_D_e_g[node_i]+1$ $displaystyle Total= N + sum_{node_i=1}^{N} Out_D_e_g[node_i]$ 哪里 全部的 表示Euler巡更树中的节点总数 node_i 表示给定树中的第i个节点 N表示给定树中的节点总数 Out_D_e_g[node_i] 表示的子对象数 node_i

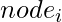
C++

// C++ program to check the number of nodes
// in Euler Tour tree.
#include <bits/stdc++.h>
using namespace std;
#define MAX 1001
// Adjacency list representation of tree
vector< int > adj[MAX];
// Function to add edges to tree
void add_edge( int u, int v)
{
adj[u].push_back(v);
}
// Program to check if calculated Value is
// equal to 2*size-1
void checkTotalNumberofNodes( int actualAnswer,
int size)
{
int calculatedAnswer = size;
// Add out-degree of each node
for ( int i = 1; i <= size; i++)
calculatedAnswer += adj[i].size();
if (actualAnswer == calculatedAnswer)
cout << "Calculated Answer is " << calculatedAnswer
<< " and is Equal to Actual Answer" ;
else
cout << "Calculated Answer is Incorrect" ;
}
int main()
{ // Constructing 1st tree from example
int N = 8;
add_edge(1, 2);
add_edge(1, 3);
add_edge(2, 4);
add_edge(2, 5);
add_edge(3, 6);
add_edge(3, 7);
add_edge(6, 8);
// Out_deg[node[i]] is equal to adj[i].size()
checkTotalNumberofNodes(2 * N - 1, N);
// clear previous stored tree
for ( int i = 1; i <= N; i++)
adj[i].clear();
// Constructing 2nd tree from example
N = 9;
add_edge(1, 2);
add_edge(1, 3);
add_edge(2, 4);
add_edge(2, 5);
add_edge(2, 6);
add_edge(3, 9);
add_edge(5, 7);
add_edge(5, 8);
// Out_deg[node[i]] is equal to adj[i].size()
checkTotalNumberofNodes(2 * N - 1, N);
return 0;
} 





               










   JAVA  












                        


        


                                                     


        


                          


        


                                                                                






















                         // Java program to check the number of nodes                       


                         // in Euler Tour tree.                       


                         import                                     java.util.*;                       


           


                         class                                     GFG                       


                         {                       


                                                 static                                     final                                     int                                     MAX =                                     1001                                     ;                       


           


                                                 // Adjacency list representation of tree                       


                                                 static                                     Vector<Integer>[] adj =                                     new                                     Vector[MAX];                       


           


                                                 // Function to add edges to tree                       


                                                 static                                     void                                     add_edge(                                     int                                     u,                                     int                                     v)                       


                                                 {                       


                                                 adj[u].add(v);                       


                                                 }                       


           


                                                 // Program to check if calculated Value is                       


                                                 // equal to 2*size-1                       


                                                 static                                     void                                     checkTotalNumberofNodes(                                     int                                     actualAnswer,                       


                                                 int                                     size)                       


                                                 {                       


                                                 int                                     calculatedAnswer = size;                       


           


                                                 // Add out-degree of each node                       


                                                 for                                     (                                     int                                     i =                                     1                                     ; i <= size; i++)                       


                                                 calculatedAnswer += adj[i].size();                       


           


                                                 if                                     (actualAnswer == calculatedAnswer)                       


                                                 System.out.print(                                     "Calculated Answer is "                                     +                       


                                                 calculatedAnswer +                       


                                                 " and is Equal to Actual Answer"                                     );                       


                                                 else                       


                                                 System.out.print(                                     "Calculated Answer is Incorrect"                                     );                       


                                                 }                       


           


                                                 // Driver Code                       


                                                 public                                     static                                     void                                     main(String[] args)                       


                                                 {                       


                                                 for                                     (                                     int                                     i =                                     0                                     ; i < MAX; i++)                       


                                                 adj[i] =                                     new                                     Vector<Integer>();                       


                                   


                                                 // Constructing 1st tree from example                       


                                                 int                                     N =                                     8                                     ;                       


                                                 add_edge(                                     1                                     ,                                     2                                     );                       


                                                 add_edge(                                     1                                     ,                                     3                                     );                       


                                                 add_edge(                                     2                                     ,                                     4                                     );                       


                                                 add_edge(                                     2                                     ,                                     5                                     );                       


                                                 add_edge(                                     3                                     ,                                     6                                     );                       


                                                 add_edge(                                     3                                     ,                                     7                                     );                       


                                                 add_edge(                                     6                                     ,                                     8                                     );                       


           


                                                 // Out_deg[node[i]] is equal to adj[i].size()                       


                                                 checkTotalNumberofNodes(                                     2                                     * N -                                     1                                     , N);                       


           


                                                 // clear previous stored tree                       


                                                 for                                     (                                     int                                     i =                                     1                                     ; i <= N; i++)                       


                                                 adj[i].clear();                       


           


                                                 // Constructing 2nd tree from example                       


                                                 N =                                     9                                     ;                       


                                                 add_edge(                                     1                                     ,                                     2                                     );                       


                                                 add_edge(                                     1                                     ,                                     3                                     );                       


                                                 add_edge(                                     2                                     ,                                     4                                     );                       


                                                 add_edge(                                     2                                     ,                                     5                                     );                       


                                                 add_edge(                                     2                                     ,                                     6                                     );                       


                                                 add_edge(                                     3                                     ,                                     9                                     );                       


                                                 add_edge(                                     5                                     ,                                     7                                     );                       


                                                 add_edge(                                     5                                     ,                                     8                                     );                       


           


                                                 // Out_deg[node[i]] is equal to adj[i].size()                       


                                                 checkTotalNumberofNodes(                                     2                                     * N -                                     1                                     , N);                       


                                                 }                       


                         }                       


           


                         // This code is contributed by Rajput-Ji                       












    






               






               










   C#  












                        


        


                                                     


        


                          


        


                                                                                






















                         // C# program to check the number                       


                         // of nodes in Euler Tour tree.                       


                         using                                     System;                       


                         using                                     System.Collections.Generic;                       


           


                         class                                     GFG                       


                         {                       


                                                 static                                     readonly                                     int                                     MAX = 1001;                       


           


                                                 // Adjacency list representation of tree                       


                                                 static                                     List<                                     int                                     >[] adj =                                     new                                     List<                                     int                                     >[MAX];                       


           


                                                 // Function to add edges to tree                       


                                                 static                                     void                                     add_edge(                                     int                                     u,                                     int                                     v)                       


                                                 {                       


                                                 adj[u].Add(v);                       


                                                 }                       


           


                                                 // Program to check if calculated Value is                       


                                                 // equal to 2*size-1                       


                                                 static                                     void                                     checkTotalNumberofNodes(                                     int                                     actualAnswer,                       


                                                 int                                     size)                       


                                                 {                       


                                                 int                                     calculatedAnswer = size;                       


           


                                                 // Add out-degree of each node                       


                                                 for                                     (                                     int                                     i = 1; i <= size; i++)                       


                                                 calculatedAnswer += adj[i].Count;                       


           


                                                 if                                     (actualAnswer == calculatedAnswer)                       


                                                 Console.Write(                                     "Calculated Answer is "                                     +                       


                                                 calculatedAnswer +                       


                                                 " and is Equal to Actual Answer"                                     );                       


                                                 else                       


                                                 Console.Write(                                     "Calculated Answer "                                     +                       


                                                 "is Incorrect"                                     );                       


                                                 }                       


           


                                                 // Driver Code                       


                                                 public                                     static                                     void                                     Main(String[] args)                       


                                                 {                       


                                                 for                                     (                                     int                                     i = 0; i < MAX; i++)                       


                                                 adj[i] =                                     new                                     List<                                     int                                     >();                       


                                   


                                                 // Constructing 1st tree from example                       


                                                 int                                     N = 8;                       


                                                 add_edge(1, 2);                       


                                                 add_edge(1, 3);                       


                                                 add_edge(2, 4);                       


                                                 add_edge(2, 5);                       


                                                 add_edge(3, 6);                       


                                                 add_edge(3, 7);                       


                                                 add_edge(6, 8);                       


           


                                                 // Out_deg[node[i]] is equal to adj[i].Count                       


                                                 checkTotalNumberofNodes(2 * N - 1, N);                       


           


                                                 // clear previous stored tree                       


                                                 for                                     (                                     int                                     i = 1; i <= N; i++)                       


                                                 adj[i].Clear();                       


           


                                                 // Constructing 2nd tree from example                       


                                                 N = 9;                       


                                                 add_edge(1, 2);                       


                                                 add_edge(1, 3);                       


                                                 add_edge(2, 4);                       


                                                 add_edge(2, 5);                       


                                                 add_edge(2, 6);                       


                                                 add_edge(3, 9);                       


                                                 add_edge(5, 7);                       


                                                 add_edge(5, 8);                       


           


                                                 // Out_deg[node[i]] is equal to adj[i].Count                       


                                                 checkTotalNumberofNodes(2 * N - 1, N);                       


                                                 }                       


                         }                       


           


                         // This code is contributed by PrinciRaj1992                       












    






               






               










   Javascript  












                        


        


                                                     


        


                          


        


                                                                                






















                         <script>                       


           


                         // Javascript program to check the number                       


                         // of nodes in Euler Tour tree.                       


                         var                                     MAX = 1001;                       


           


                         // Adjacency list representation of tree                       


                         var                                     adj = Array.from(Array(MAX), ()=>Array());                       


           


                         // Function to add edges to tree                       


                         function                                     add_edge(u, v)                       


                         {                       


                                                 adj[u].push(v);                       


                         }                       


           


                         // Program to check if calculated Value is                       


                         // equal to 2*size-1                       


                         function                                     checkTotalNumberofNodes(actualAnswer, size)                       


                         {                       


                                                 var                                     calculatedAnswer = size;                       


                                   


                                                 // push out-degree of each node                       


                                                 for                                     (                                     var                                     i = 1; i <= size; i++)                       


                                                 calculatedAnswer += adj[i].length;                       


                                                 if                                     (actualAnswer == calculatedAnswer)                       


                                                 document.write(                                     "Calculated Answer is "                                     +                       


                                                 calculatedAnswer +                       


                                                 " and is Equal to Actual Answer<br>"                                     );                       


                                                 else                       


                                                 document.write(                                     "Calculated Answer "                                     +                       


                                                 "is Incorrect<br>"                                     );                       


                         }                       


           


                         // Driver Code                       


                         for                                     (                                     var                                     i = 0; i < MAX; i++)                       


                                                 adj[i] = [];                       


                                   


                         // Constructing 1st tree from example                       


                         var                                     N = 8;                       


                         add_edge(1, 2);                       


                         add_edge(1, 3);                       


                         add_edge(2, 4);                       


                         add_edge(2, 5);                       


                         add_edge(3, 6);                       


                         add_edge(3, 7);                       


                         add_edge(6, 8);                       


           


                         // Out_deg[node[i]] is equal to adj[i].Count                       


                         checkTotalNumberofNodes(2 * N - 1, N);                       


           


                         // clear previous stored tree                       


                         for                                     (                                     var                                     i = 1; i <= N; i++)                       


                                                 adj[i] = []                       


                                   


                         // Constructing 2nd tree from example                       


                         N = 9;                       


                         add_edge(1, 2);                       


                         add_edge(1, 3);                       


                         add_edge(2, 4);                       


                         add_edge(2, 5);                       


                         add_edge(2, 6);                       


                         add_edge(3, 9);                       


                         add_edge(5, 7);                       


                         add_edge(5, 8);                       


           


                         // Out_deg[node[i]] is equal to adj[i].Count                       


                         checkTotalNumberofNodes(2 * N - 1, N);                       


           


                         // This code is contributed by itsok.                       


                         </script>                       












    






               






               












     输出：     


Calculated Answer is 15 and is Equal to Actual AnswerCalculated Answer is 17 and is Equal to Actual Answer




 


                    

        
© 版权声明
文章版权归作者所有，未经允许请勿转载。
THE END
技术文章
    

    
喜欢就支持一下吧
点赞9
        分享

        

            

                
                
CPPKU的头像-yiteyi-C++库

                
            

            
VS调试报错：f:\dd\vctools\vc7libs\ship\atlmfc\src\occcont.cpp line:925的原因-yiteyi-C++库
VS调试报错：f:\dd\vctools\vc7libs\ship\atlmfc\src\occcont.cpp line:925的原因
VS调试报错：f:\dd\vctools\vc7libs\ship\atlmfc\src\occcont.cpp li...
8年前 2.6W+
关于”PostgreSQL错误：关系[表]不存在“问题的原因和解决方案-yiteyi-C++库
关于”PostgreSQL错误：关系[表]不存在“问题的原因和解决方案
关于”PostgreSQL错误：关系[表]不存在“问题的原因和解决方案
7年前 9287
Easylogging++入门教程（三）Easylogging++ 配置-yiteyi-C++库
Easylogging++入门教程（三）Easylogging++ 配置
Easylogging++入门教程（三）Easylogging++ 配置
9年前 9056
常见的小波基函数有哪些？如何选择合适的小波基函数？-yiteyi-C++库
常见的小波基函数有哪些？如何选择合适的小波基函数？
常见的小波基函数有哪些？如何选择合适的小波基函数？
8年前 8484
TiXmlDocument变量LoadFile()加载XML文档失败的原因有哪些？-yiteyi-C++库
TiXmlDocument变量LoadFile()加载XML文档失败的原因有哪些？
TiXmlDocument变量LoadFile()加载XML文档失败的原因有哪些？
10年前 6676
Easylogging++入门教程（一）Easylogging++日志库简介-yiteyi-C++库
Easylogging++入门教程（一）Easylogging++日志库简介
Easylogging++入门教程（一）Easylogging++日志库简介
9年前 6608

        

    
    

        
    



            

                
相关推荐

            
ISRO | ISRO CS 2017 |问题6-yiteyi-C++库
ISRO | ISRO CS 2017 |问题6
ISRO | ISRO CS 2017 |问题6
3年前 477
比特屏蔽和动态编程|集1（计算方法，为每个人分配唯一的上限）-yiteyi-C++库
比特屏蔽和动态编程|集1（计算方法，为每个人分配唯一的上限）
比特屏蔽和动态编程|集1（计算方法，为每个人分配唯一的上限）
3年前 291
SAP位置编码问题-yiteyi-C++库
SAP位置编码问题
SAP位置编码问题
3年前 290
STD:：C++中的NExtx置换和Pype置换-yiteyi-C++库
STD:：C++中的NExtx置换和Pype置换
STD:：C++中的NExtx置换和Pype置换
3年前 281
2018年NSIT德里协会黑客团队Geeksforgeks-yiteyi-C++库
2018年NSIT德里协会黑客团队Geeksforgeks
2018年NSIT德里协会黑客团队Geeksforgeks
3年前 281
抗锯齿线|吴小林算法-yiteyi-C++库
抗锯齿线|吴小林算法
抗锯齿线|吴小林算法
3年前 172