Vantieghems定理 是一个数为素数的充要条件。它指出,自然数n为素数时 ![]() 哪里
哪里 ![]() ,与
,与 ![]() . 换句话说,一个数n是素数当且仅当。
. 换句话说,一个数n是素数当且仅当。 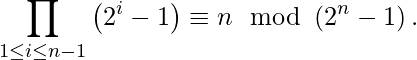 例如:
例如:
null
- 对于n=3,最终产品为(2 1. – 1) * (2 2. – 1) = 1*3 = 3. 3等于3模7。我们从表达式3*(mod(2)中得到3 mod 7 3. –1),因此3是素数。
- 对于n=5,最终产品为1*3*7*15=315。315与5(mod 31)全等,因此5是素数。
- 对于n=7,最终产品为1*3*7*15*31*63=615195。615195与7(mod 127)全等,因此7是素数。
- 对于n=4,最终产品1*3*7=21。21与4(mod 15)不一致,因此4是复合的。
说明上述定理的另一种方法是 ![]() 分裂
分裂 ![]() ,那么n是素数。
,那么n是素数。
C++
// C++ code to verify Vantieghem's Theorem #include <bits/stdc++.h> using namespace std; void checkVantieghemsTheorem( int limit) { long long unsigned prod = 1; for ( long long unsigned n = 2; n < limit; n++) { // Check if above condition is satisfied if (((prod - n) % ((1LL << n) - 1)) == 0) cout << n << " is prime" ; // product of previous powers of 2 prod *= ((1LL << n) - 1); } } // Driver code int main() { checkVantieghemsTheorem(10); return 0; } |
JAVA
// Java code to verify Vantieghem's Theorem import java.util.*; class GFG { static void checkVantieghemsTheorem( int limit) { long prod = 1 ; for ( long n = 2 ; n < limit; n++) { // Check if above condition is satisfied if (((prod - n < 0 ? 0 : prod - n) % (( 1 << n) - 1 )) == 0 ) System.out.print(n + " is prime" ); // product of previous powers of 2 prod *= (( 1 << n) - 1 ); } } // Driver code public static void main(String []args) { checkVantieghemsTheorem( 10 ); } } // This code is contributed by rutvik_56. |
Python3
# Python3 code to verify Vantieghem's Theorem def checkVantieghemsTheorem(limit): prod = 1 for n in range ( 2 , limit): # Check if above condition is satisfied if n = = 2 : print ( 2 , "is prime" ) if (((prod - n) % (( 1 << n) - 1 )) = = 0 ): print (n, "is prime" ) # Product of previous powers of 2 prod * = (( 1 << n) - 1 ) # Driver code checkVantieghemsTheorem( 10 ) # This code is contributed by shubhamsingh10 |
C#
// C# code to verify Vantieghem's Theorem using System; class GFG { static void checkVantieghemsTheorem( int limit) { long prod = 1; for ( long n = 2; n < limit; n++) { // Check if above condition is satisfied if (((prod - n < 0 ? 0 : prod - n) % ((1 << ( int )n) - 1)) == 0) Console.Write(n + " is prime" ); // product of previous powers of 2 prod *= ((1 << ( int )n) - 1); } } // Driver code public static void Main() { checkVantieghemsTheorem(10); } } // This code is contributed by pratham76. |
Javascript
<script> // Javascript code to verify Vantieghem's Theorem function checkVantieghemsTheorem( limit) { let prod = 1; for (let n = 2; n < limit; n++) { // Check if above condition is satisfied if (n == 2) document.write(2 + " is prime" + "</br>" ); if (((prod - n) % ((1 << n) - 1)) == 0) document.write( n + " is prime" + "</br>" ); // product of previous powers of 2 prod *= ((1 << n) - 1); } } // Driver Code checkVantieghemsTheorem(10); // This code is contributed by jana_sayantan. </script> |
输出:
2 is prime 3 is prime 5 is prime 7 is prime
上述代码不适用于大于11的n值。它会导致产品评估溢出。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END
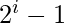


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



