分治复发的高级主定理-yiteyi-C++库

主定理用于根据渐近符号确定算法（分治算法）的运行时间。考虑使用递归求解的问题。

null

function f(input x size n)
if(n < k)
solve x directly and return 
else
divide x into a subproblems of size n/b
call f recursively to solve each subproblem
Combine the results of all sub-problems

上述算法将问题分为两部分 A. 子问题，每个子问题的大小为n/b，并递归求解，以计算问题，为问题所做的额外工作由f（n）给出，即创建子问题并将其结果合并到上述过程中的时间。

因此，根据主定理，上述算法的运行时间可以表示为：

T(n) = aT(n/b) + f(n)

其中n=问题的大小 a=递归中的子问题数，a>=1 n/b=每个子问题的大小 f（n）=在递归调用之外完成的工作成本，如划分为子问题，以及将它们组合以获得解决方案的成本。

并不是所有的递推关系都可以用主定理来解决，即如果

T（n）不是单调的，例如：T（n）=sin n
f（n）不是多项式，例如：T（n）=2T（n/2）+2 ^N

该定理是主定理的高级版本，可用于确定分治算法的运行时间，前提是递归形式如下：-

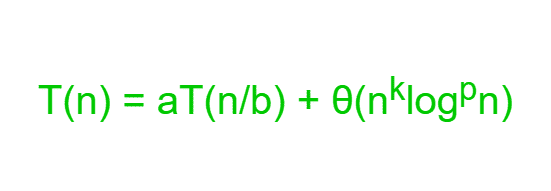
Formula to calculate runtime of divide and conquer algorithms

其中n=问题的大小 a=递归中的子问题数，a>=1 n/b=每个子问题的大小 b>1，k>=0，p是实数。

然后

如果a>b ^K ，那么T（n）=θ（n） ^日志 _^B ^A. )
如果a=b ^K 然后（a）如果p>-1，那么T（n）=θ（n） ^日志 _^B ^一日志 ^p+1 n）（b）如果p=-1，那么T（n）=θ（n） ^日志 _^B ^A. logn）（c）如果p<1，那么T（n）=θ（n） ^日志 _^B ^A. )
如果a K 然后（a）如果p>=0，那么T（n）=θ（n ^K 日志 ^P n）（b）如果p<0，那么T（n）=θ（n ^k )

时间复杂性分析-

示例1：二进制搜索- T（n）=T（n/2）+O（1） a=1、b=2、k=0和p=0 B ^K = 1. 所以，a=b ^K 和p>-1[案例2.（a）] T（n）=θ（n） ^日志 _^B ^一日志 ^p+1 n） T（n）=θ（logn）
示例2：合并排序- T（n）=2T（n/2）+O（n） a=2，b=2，k=1，p=0 B ^K = 2. 所以，a=b ^K 和p>-1[案例2.（a）] T（n）=θ（n） ^日志 _^B ^A. 日志 ^p+1 n） T（n）=θ（nlogn）
例3： T（n）=3T（n/2）+n ^2. a=3，b=2，k=2，p=0 B ^K = 4. 所以a K p=0[情况3.（a）] T（n）=θ（n） ^K 日志 ^P n） T（n）=θ（n） ² )
示例4： T（n）=3T（n/2）+对数 ^2. N a=3，b=2，k=0，p=2 B ^K = 1. 所以，a>b ^K [案例1] T（n）=θ（n） ^日志 _^B ^A. ) T（n）=θ（n） ^日志 _^2. ^3. )
例5： T（n）=2T（n/2）+nlog ^2. N a=2，b=2，k=1，p=2 b ^K = 2. 所以，a=b ^K [案例2.（a）] T（n）=θ（n） ^日志 _^B ^A. 日志 ^p+1 n） T（n）=θ（n） ^日志 _^2. ^2. 日志 ^3. n） T（n）=θ（nlog） ^3. n）
例6： T（n）=2 ^N T（n/2）+n ^N 由于函数的形式不是t（n）=aT（n/b）+θ（n），所以不能用上述方法求解这种递推 ^K 日志 ^P n）

大门练习问题-

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章