子阵中使用Mo算法的不同元素-yiteyi-C++库

给定一个大小为n的数组“a[]”和查询数q。每个查询可以由两个整数l和r表示。您的任务是打印子数组l到r中的不同整数数。给出一个[i]<= $10^6$ 例如：

null

Input : a[] = {1, 1, 2, 1, 2, 3}
        q = 3
        0 4
        1 3
        2 5
Output : 2
         2
         3
In query 1, number of distinct integers
in a[0...4] is 2 (1, 2)
In query 2, number of distinct integers 
in a[1..3] is 2 (1, 2)
In query 3, number of distinct integers 
in a[2..5] is 3 (1, 2, 3)

Input : a[] = {7, 3, 5, 9, 7, 6, 4, 3, 2}
        q = 4
        1 5
        0 4
        0 7
        1 8
output : 5
         4
         6
         7

设[0…n-1]为输入数组，q[0…m-1]为查询数组。 方法：

对所有查询进行排序，使L值从0到 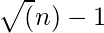$sqrt(n) - 1$ 将所有查询放在一起 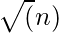$sqrt(n)$ 到 $2*sqrt(n) - 1$ 等等块内的所有查询都按R值的递增顺序排序。
初始化大小为的数组freq[] $10^6$ 0。freq[]数组记录给定范围内所有元素的频率。
一个接一个地处理所有查询，每个查询使用以前查询中计算的不同元素数和频率数组，并将结果存储在结构中。
- 让‘curr_Diff_element’是前一个查询中不同元素的数量。
- 删除上一个查询的额外元素。例如，如果上一个查询是[0,8]，而当前查询是[3,9]，则删除[0]、[1]和[2]
- 添加当前查询的新元素。在与上面相同的示例中，添加[9]。
按照前面提供的顺序对查询进行排序，并打印存储的结果

添加元素（）

将要添加的元素的频率（freq[a[i]]）增加1。
如果元素a[i]的频率为1。在范围内添加1个新元素后，将curr_diff_元素增加1。

删除元素（）

将要移除的元素的频率（a[i]）降低1。
如果元素a[i]的频率为0。只需将curr_diff_element减少1，因为1个元素已完全从范围中移除。

注：在该算法中，在第2步中，R的索引变量最多变化O（n* $sqrt(n)$ )在整个运行过程中，L的相同值最多改变O（m* $sqrt(n)$ )时报。所有这些界限都是可能的，因为排序的查询首先出现在数据块中 $sqrt(n)$ 大小

预处理部分需要O（m logm）时间。

处理所有查询需要O（n* $sqrt(n)$ )+O（m）* $sqrt(n)$ )=O（（m+n）* $sqrt(n)$ )时间。 以下是上述方法的实施情况：

                     // Program to compute no. of different elements                   
                     // of ranges for different range queries                   
                     #include <bits/stdc++.h>                   
                     using                               namespace                               std;                   
                             
                     // Used in frequency array (maximum value of an                   
                     // array element).                   
                     const                               int                               MAX = 1000000;                   
                             
                     // Variable to represent block size. This is made                   
                     // global so compare() of sort can use it.                   
                     int                               block;                   
                             
                     // Structure to represent a query range and to store                   
                     // index and result of a particular query range                   
                     struct                               Query {                   
                                         int                               L, R, index, result;                   
                     };                   
                             
                     // Function used to sort all queries so that all queries                   
                     // of same block are arranged together and within a block,                   
                     // queries are sorted in increasing order of R values.                   
                     bool                               compare(Query x, Query y)                   
                     {                   
                                         // Different blocks, sort by block.                   
                                         if                               (x.L / block != y.L / block)                   
                                         return                               x.L / block < y.L / block;                   
                             
                                         // Same block, sort by R value                   
                                         return                               x.R < y.R;                   
                     }                   
                             
                     // Function used to sort all queries in order of their                   
                     // index value so that results of queries can be printed                   
                     // in same order as of input                   
                     bool                               compare1(Query x, Query y)                   
                     {                   
                                         return                               x.index < y.index;                   
                     }                   
                             
                     // calculate distinct elements of all query ranges.                   
                     // m is number of queries n is size of array a[].                   
                     void                               queryResults(                               int                               a[],                               int                               n, Query q[],                               int                               m)                   
                     {                   
                                         // Find block size                   
                                         block = (                               int                               )                               sqrt                               (n);                   
                             
                                         // Sort all queries so that queries of same                   
                                         // blocks are arranged together.                   
                                         sort(q, q + m, compare);                   
                             
                                         // Initialize current L, current R and current                   
                                         // different elements                   
                                         int                               currL = 0, currR = 0;                   
                                         int                               curr_Diff_elements = 0;                   
                             
                                         // Initialize frequency array with 0                   
                                         int                               freq[MAX] = { 0 };                   
                             
                                         // Traverse through all queries                   
                                         for                               (                               int                               i = 0; i < m; i++) {                   
                             
                                         // L and R values of current range                   
                                         int                               L = q[i].L, R = q[i].R;                   
                             
                                         // Remove extra elements of previous range.                   
                                         // For example if previous range is [0, 3]                   
                                         // and current range is [2, 5], then a[0]                   
                                         // and a[1] are subtracted                   
                                         while                               (currL < L) {                   
                             
                                         // element a[currL] is removed                   
                                         freq[a[currL]]--;                   
                                         if                               (freq[a[currL]] == 0)                   
                                         curr_Diff_elements--;                   
                             
                                         currL++;                   
                                         }                   
                             
                                         // Add Elements of current Range                   
                                         // Note:- during addition of the left                   
                                         // side elements we have to add currL-1                   
                                         // because currL is already in range                   
                                         while                               (currL > L) {                   
                                         freq[a[currL - 1]]++;                   
                             
                                         // include a element if it occurs first time                   
                                         if                               (freq[a[currL - 1]] == 1)                   
                                         curr_Diff_elements++;                   
                             
                                         currL--;                   
                                         }                   
                                         while                               (currR <= R) {                   
                                         freq[a[currR]]++;                   
                             
                                         // include a element if it occurs first time                   
                                         if                               (freq[a[currR]] == 1)                   
                                         curr_Diff_elements++;                   
                             
                                         currR++;                   
                                         }                   
                             
                                         // Remove elements of previous range. For example                   
                                         // when previous range is [0, 10] and current range                   
                                         // is [3, 8], then a[9] and a[10] are subtracted                   
                                         // Note:- Basically for a previous query L to R                   
                                         // currL is L and currR is R+1. So during removal                   
                                         // of currR remove currR-1 because currR was                   
                                         // never included                   
                                         while                               (currR > R + 1) {                   
                             
                                         // element a[currL] is removed                   
                                         freq[a[currR - 1]]--;                   
                             
                                         // if occurrence of a number is reduced                   
                                         // to zero remove it from list of                   
                                         // different elements                   
                                         if                               (freq[a[currR - 1]] == 0)                   
                                         curr_Diff_elements--;                   
                             
                                         currR--;                   
                                         }                   
                                         q[i].result = curr_Diff_elements;                   
                                         }                   
                     }                   
                             
                     // print the result of all range queries in                   
                     // initial order of queries                   
                     void                               printResults(Query q[],                               int                               m)                   
                     {                   
                                         sort(q, q + m, compare1);                   
                                         for                               (                               int                               i = 0; i < m; i++) {                   
                                         cout <<                               "Number of different elements"                               <<                   
                                         " in range "                               << q[i].L <<                               " to "                   
                                         << q[i].R <<                               " are "                               << q[i].result << endl;                   
                                         }                   
                     }                   
                             
                     // Driver program                   
                     int                               main()                   
                     {                   
                                         int                               a[] = { 1, 1, 2, 1, 3, 4, 5, 2, 8 };                   
                                         int                               n =                               sizeof                               (a) /                               sizeof                               (a[0]);                   
                                         Query q[] = { { 0, 4, 0, 0 }, { 1, 3, 1, 0 },                   
                                         { 2, 4, 2, 0 } };                   
                                         int                               m =                               sizeof                               (q) /                               sizeof                               (q[0]);                   
                                         queryResults(a, n, q, m);                   
                                         printResults(q, m);                   
                                         return                               0;                   
                     }                   

输出：

Number of different elements in range 0 to 4 are 3
Number of different elements in range 1 to 3 are 2
Number of different elements in range 2 to 4 are 3

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章