从特定节点开始的大小为k的循环数-yiteyi-C++库

给定两个正整数 n、 k 考虑完全连通图中n个结点的无向完全连通图。任务是计算从任何节点开始并通过访问K个节点返回的方式的数量。例如：

null

Input : n = 3, k = 3
Output : 2

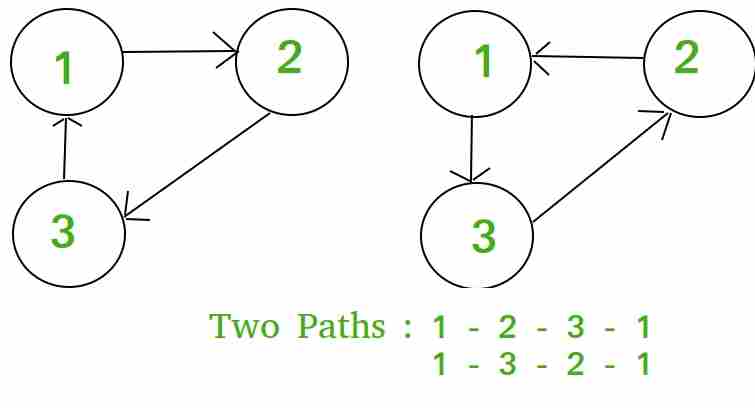
Number of loops of size k starting from a specific node

Input : n = 4, k = 2
Output : 3

推荐：请尝试你的方法 {IDE} 首先，在进入解决方案之前。

让 f（n，k） 这是一个函数，它返回从任何节点开始并通过访问K个节点返回的多种方式。如果我们从一个节点开始和结束，那么我们要为中间节点做K–1选择，因为我们已经在开始时选择了一个节点。对于每个中间选项，您有n–1个选项。因此，这将产生（n–1） ^k-1 但是我们必须去掉所有的选择，因为循环更小，所以我们减去 f（n，k-1） . 所以，递归关系变成， f（n，k）=（n-1） ^k-1 -f（n，k-1），基本情况为f（n，2）=n-1。关于扩张， f（n，k）=（n-1） ^k-1 –（n–1） ^k-2 +（n-1） ^k-3 ….. （n–1）（如等式1所示）将f（n，k）除以（n-1）， f（n，k）/（n-1）=（n-1） ^k-2 –（n–1） ^k-3 +（n-1） ^k-4 ….. 1（比如等式2）在添加等式1和等式2时， f（n，k）+f（n，k）/（n-1）=（n-1） ^k-1 + (-1) ^K f（n，k）*（（n-1）+1）/（n-1）=（n-1） ^k-1 + (-1) ^K $f(n, k) = frac{(n-1)^{k} + (-1)^{k}(n-1)}{n}$ 以下是该方法的实施情况：

C++

                         // C++ Program to find number of cycles of length                       
                         // k in a graph with n nodes.                       
                         #include <bits/stdc++.h>                       
                         using                                     namespace                                     std;                       
                                   
                         // Return the Number of ways from a                       
                         // node to make a loop of size K in undirected                       
                         // complete connected graph of N nodes                       
                         int                                     numOfways(                                     int                                     n,                                     int                                     k)                       
                         {                       
                                                 int                                     p = 1;                       
                                   
                                                 if                                     (k % 2)                       
                                                 p = -1;                       
                                   
                                                 return                                     (                                     pow                                     (n - 1, k) + p * (n - 1)) / n;                       
                         }                       
                                   
                         // Driven Program                       
                         int                                     main()                       
                         {                       
                                                 int                                     n = 4, k = 2;                       
                                                 cout << numOfways(n, k) << endl;                       
                                                 return                                     0;                       
                         }                       

JAVA

                         // Java Program to find number of                       
                         // cycles of length k in a graph                       
                         // with n nodes.                       
                         public                                     class                                     GFG {                       
                                   
                                                 // Return the Number of ways                       
                                                 // from a node to make a loop                       
                                                 // of size K in undirected                       
                                                 // complete connected graph of                       
                                                 // N nodes                       
                                                 static                                     int                                     numOfways(                                     int                                     n,                                     int                                     k)                       
                                                 {                       
                                                 int                                     p =                                     1                                     ;                       
                                   
                                                 if                                     (k %                                     2                                     !=                                     0                                     )                       
                                                 p = -                                     1                                     ;                       
                                   
                                                 return                                     (                                     int                                     )(Math.pow(n -                                     1                                     , k)                       
                                                 + p * (n -                                     1                                     )) / n;                       
                                                 }                       
                                   
                                                 // Driver code                       
                                                 public                                     static                                     void                                     main(String args[])                       
                                                 {                       
                                                 int                                     n =                                     4                                     , k =                                     2                                     ;                       
                                   
                                                 System.out.println(numOfways(n, k));                       
                                                 }                       
                         }                       
                                   
                         // This code is contributed by Sam007.                       

Python3

                         # python Program to find number of                       
                         # cycles of length k in a graph                       
                         # with n nodes.                       
                                   
                         # Return the Number of ways from a                       
                         # node to make a loop of size K in                       
                         # undirected complete connected                       
                         # graph of N nodes                       
                         def                                     numOfways(n,k):                       
                                   
                                                 p                                     =                                     1                       
                                   
                                                 if                                     (k                                     %                                     2                                     ):                       
                                                 p                                     =                                     -                                     1                       
                                   
                                                 return                                     (                                     pow                                     (n                                     -                                     1                                     , k)                                     +                       
                                                 p                                     *                                     (n                                     -                                     1                                     ))                                     /                                     n                       
                                   
                         # Driver code                       
                         n                                     =                                     4                       
                         k                                     =                                     2                       
                         print                                     (numOfways(n, k))                       
                                   
                         # This code is contributed by Sam007.                       

C#

                         // C# Program to find number of cycles                       
                         // of length k in a graph with n nodes.                       
                         using                                     System;                       
                                   
                         class                                     GFG {                       
                                   
                                                 // Return the Number of ways from                       
                                                 // a node to make a loop of size                       
                                                 // K in undirected complete                       
                                                 // connected graph of N nodes                       
                                                 static                                     int                                     numOfways(                                     int                                     n,                                     int                                     k)                       
                                                 {                       
                                                 int                                     p = 1;                       
                                   
                                                 if                                     (k % 2 != 0)                       
                                                 p = -1;                       
                                   
                                                 return                                     (                                     int                                     )(Math.Pow(n - 1, k)                       
                                                 + p * (n - 1)) / n;                       
                                                 }                       
                                   
                                                 // Driver code                       
                                                 static                                     void                                     Main()                       
                                                 {                       
                                                 int                                     n = 4, k = 2;                       
                                   
                                                 Console.Write( numOfways(n, k) );                       
                                                 }                       
                         }                       
                                   
                         // This code is contributed by Sam007.                       

PHP

                         <?php                       
                         // PHP Program to find number                       
                         // of cycles of length                       
                         // k in a graph with n nodes.                       
                                   
                         // Return the Number of ways from a                       
                         // node to make a loop of size K                       
                         // in undirected complete connected                       
                         // graph of N nodes                       
                         function                                     numOfways(                                     $n                                     ,                                     $k                                     )                       
                         {                       
                         $p                                     = 1;                       
                                   
                         if                                     (                                     $k                                     % 2)                       
                                                 $p                                     = -1;                       
                                   
                         return                                     (pow(                                     $n                                     - 1,                                     $k                                     ) +                       
                                                 $p                                     * (                                     $n                                     - 1)) /                                     $n                                     ;                       
                         }                       
                                   
                                                 // Driver Code                       
                                                 $n                                     = 4;                       
                                                 $k                                     = 2;                       
                                                 echo                                     numOfways(                                     $n                                     ,                                     $k                                     );                       
                                   
                         // This code is contributed by vt_m.                       
                         ?>                       

Javascript

                         <script>                       
                                   
                         // JavaScript Program to find number of                       
                         // cycles of length k in a graph                       
                         // with n nodes.                       
                                   
                                                 // Return the Number of ways                       
                                                 // from a node to make a loop                       
                                                 // of size K in undirected                       
                                                 // complete connected graph of                       
                                                 // N nodes                       
                                                 function                                     numOfways(n, k)                       
                                                 {                       
                                                 let p = 1;                       
                                   
                                                 if                                     (k % 2 != 0)                       
                                                 p = -1;                       
                                   
                                                 return                                     (Math.pow(n - 1, k)                       
                                                 + p * (n - 1)) / n;                       
                                                 }                       
                                   
                         // Driver code                       
                                                 let n = 4, k = 2;                       
                                                 document.write(numOfways(n, k));                       
                                   
                                                 // This code is contributed by code_hunt.                       
                         </script>                       

输出：

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章