公钥密码学也称为非对称密码学,是一种涉及使用两种密钥的密码学,即公钥和私钥。接收方的公钥用于加密发送方的明文,而接收方的私钥用于解密加密的消息,因此只能由预期接收方解密。 RSA(Rivest-Shamir-Adleman)是一种公钥密码算法,其中密钥生成基于两个大素数p和q的乘积,从而生成N,即N=p×q。该算法的安全性关键在于攻击者需要首先通过指数时间内发生的N的因式分解找到p和q。研究表明,如果N是100位数字,这可能需要70多年的时间。由于这种复杂性,攻击者无法找到解密密钥d,因为d依赖于p、q和加密密钥e。因此,即使攻击者知道N和e,也无法计算d。
RSA的当前场景: 截至2017年4月,RSA-2048在未来许多年内可能无法分解。此外,最近的 勒索软件 该病毒还使用RSA-2048加密受感染系统上的文件。如果没有解密密钥,这些文件就无法解密,因为如此大的密钥无法分解。因此,RSA-1024和RSA-2048现在被广泛用于安全通信。
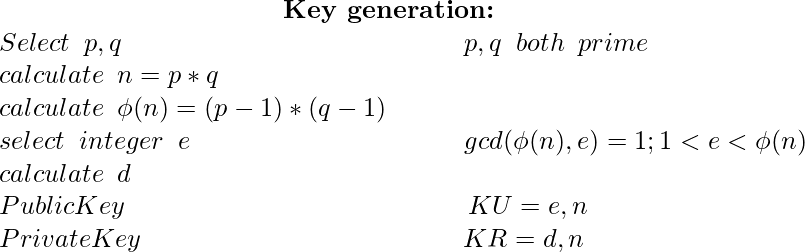

上图显示了RSA算法的三个不同阶段。考虑到素数生成器生成1024位素数p和q,结果N将是2048位的数。由于在加密和解密期间执行的所有模运算都与N有关,N是2048位的数字,因此这一操作的软件实现可能非常耗时。此外,C的无符号长整型数据类型将计算限制为64位数字。为了支持根据RSA算法的要求生成大尺寸密钥,以及快速计算涉及大尺寸模数的加密和解密,可以使用一个名为GMP(GNU多精度算术库)的库。使用该库将允许整个RSA算法在简单的64位操作系统上运行,从而避免使用超级计算机或高配置硬件设备。
什么是GMP? GMP 是一个开源库,它允许对有符号整数、有理数和十进制数执行算术计算,而不受其精度的任何实际限制,除了运行它的机器的配置之外。该库用于涉及非常大或高精度数字的算术计算,其中大多数用于加密算法。使用该库的好处是,它支持任意精度的数字,而在执行程序之前,这些数字的大小是未知的。为使用该库而提供的基本接口适用于C语言。但是,包装语言存在于其他语言中,包括艾达、C++、C**、朱丽亚、OcAML、Perl、PHP、Python、R、露比和WordFrm语言。 作为一个例子,下面提到一个执行两个多精度数乘法的C程序。 笔记 这就是gmp。h文件需要作为头文件包含。可以使用以下命令在Unix系统上编译这样的程序
gcc program_name.c -lgmp
C
#include <stdio.h> #include <gmp.h> int main( void ) { mpz_t x, y, result; mpz_init_set_str(x, "7612058254738945" , 10); mpz_init_set_str(y, "9263591128439081" , 10); mpz_init(result); mpz_mul(result, x, y); gmp_printf( " %Zd" "*" " %Zd" "--------------------" "%Zd" , x, y, result); /* free used memory */ mpz_clear(x); mpz_clear(y); mpz_clear(result); return 0; } |
对RSA算法进行编码: 一个C程序描述了小素数RSA算法的工作原理 在这里 .为了了解实数RSA算法使用大素数的工作原理,我们提供了一个使用GMP库的C代码 在这里 该程序通过生成512位的随机素数p和q,然后进行加密和解密,来实现RSA-1024。这里,可变模数_大小被分配值1024。该值可以更改为2048,以生成2048位的RSA密钥。
应用: RSA算法已被广泛应用于许多电子商务应用的安全网络通信和安全交易中。其他应用包括通过低比特率信道进行语音通信、甚至高速IPSec的安全密钥交换、与在线商家通信时的信用卡详细信息等。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



