文本由字符A、b、c、d、e组成,每个字符出现的概率分别为0.11、0.40、0.16、0.09和0.24。最佳哈夫曼编码技术的平均长度为: (A) 2.40 (B) 2.16 (C) 2.26 (D) 2.15 答复: (B) 说明: a=0.11 b=0.40 c=0.16 d=0.09 e=0.24 我们将画一棵哈夫曼树: 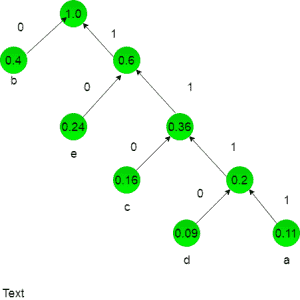
null
现在,哈夫曼为角色编码:
a = 1111
b = 0
c = 110
d = 1111
e = 10
lenghth for each character = no of bits * frequency of occurence:
a = 4 * 0.11
= 0.44
b = 1 * 0.4
= 0.4
c = 3 * 0.16
= 0.48
d = 4 * 0.09
= 0.36
e = 2 * 0.24
= 0.48
Now add these lenght for average length:
0.44 + 0.4 + 0.48 + 0.36 + 0.48 = 2.16
因此,选项(B)是正确的。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



