下推自动机最终状态验收

我们讨论了下推自动机（PDA）及其应用 空堆验收 文章现在，在本文中，我们将讨论PDA如何接受基于最终状态的CFL。给定PDA P作为：

P = (Q, Σ, Γ, δ, q0, Z, F)

P所接受的语言是所有字符串的集合，PDA可以从初始状态移动到最终状态，而不考虑堆栈上剩余的任何符号，这些符号可以描述为：

L(P) = {w |(q0, w, Z) =>(qf, ɛ, s)}

这里，从开始状态q0和堆栈符号Z开始，当消耗输入w时，达到最终状态qfɛF。堆栈可以包含字符串s，当到达最终状态时，字符串s是无关的，而w将被接受。

例子： 使用final state为语言{a^nb^n |n>0}定义下推自动机。 解决方案： M=其中Q={q0，q1，q2，q3}和∑ = {a，b}和Γ={a，Z}和F={q3}和δ由下式给出：

δ( q0, a, Z ) = { ( q1, AZ ) }
δ( q1, a, A) = { ( q1, AA ) }
δ( q1, b, A) = { ( q2, ɛ) }
δ( q2, b, A) = { ( q2, ɛ) }
δ( q2, ɛ, Z) = { ( q3, Z) }

让我们看看这个自动机是如何为aaabbb工作的：

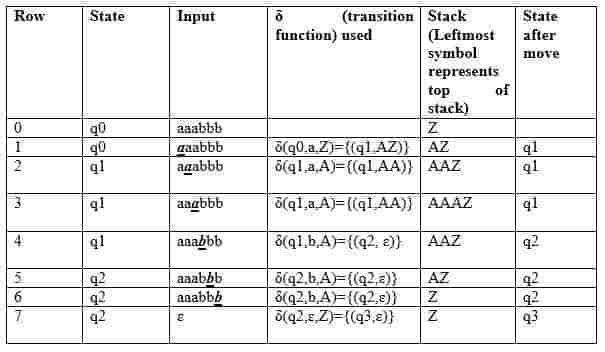
说明： 最初，自动机的状态是q0，堆栈上的符号是Z，输入是aaabbb，如第0行所示。读取a时（第1行以粗体显示），状态将更改为q1，并将符号a推送到堆栈上。在下一个a（如第2行所示）上，它将把另一个符号a推到堆栈上，并保持状态q1。读取3 a后，堆栈将为AAAZ，顶部为a。

读取b（如第4行所示）后，它将弹出A并移动到状态q2，堆栈将为AAZ。当读取所有b时，状态将为q2，堆栈将为Z。在第7行，在堆栈上的输入符号ɛ和Z上，它将移动到q3。由于处理输入后已达到最终状态q3，因此将接受字符串。 这种类型的验收被称为 最终国家的接受 .

接下来，我们将了解该自动机如何为aab工作：

如第4行所示，输入已被处理，PDA处于非最终状态q2，字符串aab将不被接受。

让我们在此基础上讨论这个问题：

Que-1。 考虑下面给出的PDA的转换图，输入字母表和；{a，b}和堆栈字母Γ={X，Z}。Z是初始堆栈符号。让我表示PDA接受的语言。（GATE-CS-2016）

解决方案： 我们首先将给定PDA的状态标记为：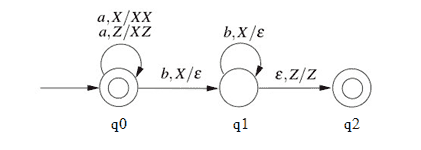

接下来，给定的PDA P可以写为：

 Q = {q0, q1, q2} and ∑ = {a, b} 
And Γ = {A, Z} and F={q0,q2} and δ is given by :
δ( q0, a, Z ) = {( q0, XZ)}
δ( q0, a, X) = {( q0, XX )}
δ( q0, b, X) = {( q1, ɛ)}
δ( q1, b, X) = {( q1, ɛ)}
δ( q1, ɛ, Z) = {( q2, Z)}

正如我们所见，q0是初始状态和最终状态，ɛ将被接受。对于每个a，X被推到堆栈上，PDA保持最终状态。因此，PDA可以接受任意数量的a。

如果输入包含b，则每个b从堆栈中弹出X。然后，如果堆栈在处理输入后变为空（δ（q1，ɛ，Z）={（q2，Z）}），则PDA将移动到最终状态。因此，如果存在，b的数量必须等于a的数量。

由于给定状态和输入只有一次移动，PDA是确定的。所以，正确的选项是（D）。