给定一个由N个整数组成的数组,在元素之间使用“+”和“-”检查是否有方法形成一个数字序列,该序列的计算结果为可被M整除的数字
例如:
输入: arr={1,2,3,4,6} M=4 输出: 符合事实的 说明: 有一个有效的序列,即(1-2) +3+4+6),其计算结果为12 可以被4整除
输入: arr={1,3,9} M=2 输出: 错误的 说明: 没有计算为的序列 可被M整除的数。
A. 简单解决方案 是递归地考虑所有可能的方案(即使用a;+)。或者在元素之间使用“-”运算符,并保持存储结果的变量和。如果这个结果可以被M整除,则返回true,否则返回false。
递归实现如下所示:
C++
bool isPossible( int index, int sum) { // Base case if (index == n) { // check if sum is divisible by M if ((sum % M) == 0) return true ; return false ; } // recursively call by considering '+' // or '-' between index and index+1 // 1.Try placing '+' bool placeAdd = isPossible(index + 1, sum + arr[index]); // 2. Try placing '-' bool placeMinus = isPossible(index + 1, sum - arr[index]); if (placeAdd || placeMinus) return true ; return false ; } |
JAVA
static boolean isPossible( int index, int sum) { // Base case if (index == n) { // Check if sum is divisible by M if ((sum % M) == 0 ) return true ; return false ; } // Recursively call by considering '+' // or '-' between index and index+1 // 1.Try placing '+' boolean placeAdd = isPossible(index + 1 , sum + arr[index]); // 2. Try placing '-' boolean placeMinus = isPossible(index + 1 , sum - arr[index]); if (placeAdd || placeMinus) return true ; return false ; } // This code is contributed by rutvik_56. |
Python3
def isPossible(index, sum ): # Base case if (index = = n): # check if sum is divisible by M if (( sum % M) = = 0 ): return True ; return False ; # recursively call by considering '+' # or '-' between index and index+1 # 1.Try placing '+' placeAdd = isPossible(index + 1 , sum + arr[index]); # 2. Try placing '-' placeMinus = isPossible(index + 1 , sum - arr[index]); if (placeAdd or placeMinus): return True ; return False ; # This code is contributed by pratham76. |
C#
static bool isPossible( int index, int sum) { // Base case if (index == n) { // Check if sum is divisible by M if ((sum % M) == 0) return true ; return false ; } // Recursively call by considering '+' // or '-' between index and index+1 // 1.Try placing '+' bool placeAdd = isPossible(index + 1, sum + arr[index]); // 2. Try placing '-' bool placeMinus = isPossible(index + 1, sum - arr[index]); if (placeAdd || placeMinus) return true ; return false ; } // This code is contributed by divyesh072019 |
Javascript
<script> function isPossible(index , sum) { // Base case if (index == n) { // Check if sum is divisible by M if ((sum % M) == 0) return true ; return false ; } // Recursively call by considering '+' // or '-' between index and index+1 // 1.Try placing '+' let placeAdd = isPossible(index + 1, sum + arr[index]); // 2. Try placing '-' let placeMinus = isPossible(index + 1, sum - arr[index]); if (placeAdd || placeMinus) return true ; return false ; } // This code is contributed by Amit Katiyar </script> |
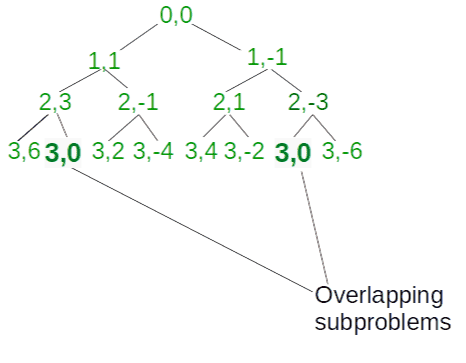
有重叠的子问题,如下图所示(注:图中表示递归树,直到索引=3)
更好的方法: 要优化上述方法,请使用动态规划。
方法1: 我们采用两种状态的动态规划:- (i) 索引, (ii)总额 所以DP[index][sum]存储我们当前的索引,sum存储在该索引之前形成的序列的评估结果。
以下是上述方法的实施情况:
C++
// C++ program to check if any // valid sequence is divisible by M #include <bits/stdc++.h> using namespace std; const int MAX = 1000; bool isPossible( int n, int index, int sum, int M, int arr[], int dp[][MAX]) { // Base case if (index == n) { // check if sum is divisible by M if ((sum % M) == 0) return true ; return false ; } // check if the current state // is already computed if (dp[index][sum] != -1) return dp[index][sum]; // 1.Try placing '+' bool placeAdd = isPossible(n, index + 1, sum + arr[index], M, arr, dp); // 2. Try placing '-' bool placeMinus = isPossible(n, index + 1, sum - arr[index], M, arr, dp); // calculate value of res for recursive case bool res = (placeAdd || placeMinus); // store the value for res for current // states and return for parent call dp[index][sum] = res; return res; } int main() { int arr[] = { 1, 2, 3, 4, 6 }; int n = sizeof (arr)/ sizeof (arr[0]); int M = 4; int dp[n + 1][MAX]; memset (dp, -1, sizeof (dp)); bool res; res = isPossible(n, 0, 0, M, arr, dp); cout << (res ? "True" : "False" ) << endl; return 0; } |
JAVA
// Java program to check if any // valid sequence is divisible by M import java.util.*; class GFG { static final int MAX = 1000 ; static boolean isPossible( int n, int index, int sum, int M, int arr[], int dp[][]) { // Base case if (index == n) { // check if sum is divisible by M if ((sum % M) == 0 ) return true ; return false ; } else if (sum < 0 || sum >= MAX) return false ; // check if the current state // is already computed if (dp[index][sum] != - 1 ) { if (dp[index][sum] == 0 ) return false ; return true ; } // 1.Try placing '+' boolean placeAdd = isPossible(n, index + 1 , sum + arr[index], M, arr, dp); // 2. Try placing '-' boolean placeMinus = isPossible(n, index + 1 , sum - arr[index], M, arr, dp); // calculate value of res for recursive case boolean res = (placeAdd || placeMinus); // store the value for res for current // states and return for parent call dp[index][sum] = (res) ? 1 : 0 ; return res; } // Driver code public static void main(String args[]) { int arr[] = { 1 , 2 , 3 , 4 , 6 }; int n = arr.length; int M = 4 ; int dp[][] = new int [n + 1 ][MAX]; for ( int i = 0 ; i < n + 1 ; i++) Arrays.fill(dp[i], - 1 ); boolean res; res = isPossible(n, 0 , 0 , M, arr, dp); System.out.println((res ? "True" : "False" )); } } // This code is contributed by ghanshyampandey |
Python3
# Python3 program to check if any # valid sequence is divisible by M def isPossible(n, index, Sum , M, arr, dp): global MAX # Base case if index = = n: # check if sum is divisible by M if ( Sum % M) = = 0 : return True return False # check if the current state # is already computed if dp[index][ Sum ] ! = - 1 : return dp[index][ Sum ] # 1.Try placing '+' placeAdd = isPossible(n, index + 1 , Sum + arr[index], M, arr, dp) # 2. Try placing '-' placeMinus = isPossible(n, index + 1 , Sum - arr[index], M, arr, dp) # calculate value of res for recursive case res = placeAdd or placeMinus # store the value for res for current # states and return for parent call dp[index][ Sum ] = res return res MAX = 1000 arr = [ 1 , 2 , 3 , 4 , 6 ] n = len (arr) M = 4 dp = [[ - 1 ] * MAX for i in range (n + 1 )] res = isPossible(n, 0 , 0 , M, arr, dp) if res: print ( True ) else : print ( False ) # this code is contributed by PranchalK |
C#
// C# program to check if any // valid sequence is divisible by M using System; class GFG { static int MAX = 1000; static Boolean isPossible( int n, int index, int sum, int M, int []arr, int [,]dp) { // Base case if (index == n) { // check if sum is divisible by M if ((sum % M) == 0) return true ; return false ; } else if (sum < 0 || sum >= MAX) return false ; // check if the current state // is already computed if (dp[index,sum] != -1) { if (dp[index,sum] == 0) return false ; return true ; } // 1.Try placing '+' Boolean placeAdd = isPossible(n, index + 1, sum + arr[index], M, arr, dp); // 2. Try placing '-' Boolean placeMinus = isPossible(n, index + 1, sum - arr[index], M, arr, dp); // calculate value of res for recursive case Boolean res = (placeAdd || placeMinus); // store the value for res for current // states and return for parent call dp[index,sum] = (res) ? 1 : 0; return res; } // Driver code public static void Main(String []args) { int []arr = { 1, 2, 3, 4, 6 }; int n = arr.Length; int M = 4; int [,]dp = new int [n + 1, MAX]; for ( int i = 0; i < n + 1; i++) for ( int j = 0; j < MAX; j++) dp[i, j] = -1; Boolean res; res = isPossible(n, 0, 0, M, arr, dp); Console.WriteLine((res ? "True" : "False" )); } } // This code is contributed by PrinciRaj1992 |
Javascript
<script> // javascript program to check if any // valid sequence is divisible by M var MAX = 1000; function isPossible(n , index , sum,M , arr , dp) { // Base case if (index == n) { // check if sum is divisible by M if ((sum % M) == 0) return true ; return false ; } else if (sum < 0 || sum >= MAX) return false ; // check if the current state // is already computed if (dp[index][sum] != -1) { if (dp[index][sum] == 0) return false ; return true ; } // 1.Try placing '+' var placeAdd = isPossible(n, index + 1, sum + arr[index], M, arr, dp); // 2. Try placing '-' var placeMinus = isPossible(n, index + 1, sum - arr[index], M, arr, dp); // calculate value of res for recursive case var res = (placeAdd || placeMinus); // store the value for res for current // states and return for parent call dp[index][sum] = (res) ? 1 : 0; return res; } // Driver code var arr = [ 1, 2, 3, 4, 6 ]; var n = arr.length; var M = 4; var dp = Array(n+1).fill(-1).map(x => Array(MAX).fill(-1)); res = isPossible(n, 0, 0, M, arr, dp); document.write((res ? "True" : "False" )); // This code contributed by shikhasingrajput </script> |
True
时间复杂性: O(N*sum),其中sum是整数序列的最大可能和,N是数组中的元素数。
方法2(高效): 这比方法1更有效。在这里,我们也应用了动态规划,但有两种不同的状态: (i) 索引, (ii)模 所以DP[index][modulo]存储序列评估结果的模,直到该指数,M。
以下是上述方法的实施情况:
C++
#include <bits/stdc++.h> using namespace std; const int MAX = 100; int isPossible( int n, int index, int modulo, int M, int arr[], int dp[][MAX]) { // Calculate modulo for this call modulo = ((modulo % M) + M) % M; // Base case if (index == n) { // check if sum is divisible by M if (modulo == 0) return 1; return 0; } // check if the current state is // already computed if (dp[index][modulo] != -1) return dp[index][modulo]; // 1.Try placing '+' int placeAdd = isPossible(n, index + 1, modulo + arr[index], M, arr, dp); // 2. Try placing '-' int placeMinus = isPossible(n, index + 1, modulo - arr[index], M, arr, dp); // calculate value of res for recursive // case bool res = (placeAdd || placeMinus); // store the value for res for current // states and return for parent call dp[index][modulo] = res; return res; } int main() { int arr[] = { 1, 2, 3, 4, 6 }; int n = sizeof (arr)/ sizeof (arr[0]); int M = 4; // MAX is the Maximum value M can take int dp[n + 1][MAX]; memset (dp, -1, sizeof (dp)); bool res; res = isPossible(n, 1, arr[0], M, arr, dp); cout << (res ? "True" : "False" ) << endl; return 0; } |
JAVA
// Java implementation of above approach class GFG { static int MAX = 100 ; static int isPossible( int n, int index, int modulo, int M, int arr[], int dp[][]) { // Calculate modulo for this call modulo = ((modulo % M) + M) % M; // Base case if (index == n) { // check if sum is divisible by M if (modulo == 0 ) { return 1 ; } return 0 ; } // check if the current state is // already computed if (dp[index][modulo] != - 1 ) { return dp[index][modulo]; } // 1.Try placing '+' int placeAdd = isPossible(n, index + 1 , modulo + arr[index], M, arr, dp); // 2. Try placing '-' int placeMinus = isPossible(n, index + 1 , modulo - arr[index], M, arr, dp); // calculate value of res for // recursive case int res = placeAdd; // store the value for res for current // states and return for parent call dp[index][modulo] = res; return res; } // Driver code public static void main(String[] args) { int arr[] = { 1 , 2 , 3 , 4 , 6 }; int n = arr.length; int M = 4 ; // MAX is the Maximum value M can take int dp[][] = new int [n + 1 ][MAX]; for ( int i = 0 ; i < n + 1 ; i++) { for ( int j = 0 ; j < MAX; j++) { dp[i][j] = - 1 ; } } boolean res; if (isPossible(n, 1 , arr[ 0 ], M, arr, dp) == 1 ) { res = true ; } else { res = false ; } System.out.println(res ? "True" : "False" ); } } // This code is contributed by // PrinciRaj1992 |
Python3
# Python3 Program to Check if any # valid sequence is divisible by M MAX = 100 def isPossible(n, index, modulo, M, arr, dp): # Calculate modulo for this call modulo = ((modulo % M) + M) % M # Base case if (index = = n): # check if sum is divisible by M if (modulo = = 0 ): return 1 return 0 # check if the current state is # already computed if (dp[index][modulo] ! = - 1 ): return dp[index][modulo] # 1.Try placing '+' placeAdd = isPossible(n, index + 1 , modulo + arr[index], M, arr, dp) # 2. Try placing '-' placeMinus = isPossible(n, index + 1 , modulo - arr[index], M, arr, dp) # calculate value of res # for recursive case res = bool (placeAdd or placeMinus) # store the value for res for current # states and return for parent call dp[index][modulo] = res return res # Driver code arr = [ 1 , 2 , 3 , 4 , 6 ] n = len (arr) M = 4 # MAX is the Maximum value # M can take dp = [[ - 1 ] * (n + 1 )] * MAX res = isPossible(n, 1 , arr[ 0 ], M, arr, dp) if (res = = True ): print ( "True" ) else : print ( "False" ) # This code is contributed by ash264 |
C#
// C# implementation of above approach using System; class GFG { static int MAX = 100; static int isPossible( int n, int index, int modulo, int M, int []arr, int [,]dp) { // Calculate modulo for this call modulo = ((modulo % M) + M) % M; // Base case if (index == n) { // check if sum is divisible by M if (modulo == 0) { return 1; } return 0; } // check if the current state is // already computed if (dp[index, modulo] != -1) { return dp[index, modulo]; } // 1.Try placing '+' int placeAdd = isPossible(n, index + 1, modulo + arr[index], M, arr, dp); // 2. Try placing '-' int placeMinus = isPossible(n, index + 1, modulo - arr[index], M, arr, dp); // calculate value of res for // recursive case int res = placeAdd; // store the value for res for current // states and return for parent call dp[index, modulo] = res; return res; } // Driver code public static void Main() { int []arr = {1, 2, 3, 4, 6}; int n = arr.Length; int M = 4; // MAX is the Maximum value M can take int [,]dp = new int [n + 1,MAX]; for ( int i = 0; i < n + 1; i++) { for ( int j = 0; j < MAX; j++) { dp[i, j] = -1; } } bool res; if (isPossible(n, 1, arr[0], M, arr, dp) == 1) { res = true ; } else { res = false ; } Console.WriteLine(res ? "True" : "False" ); } } //This code is contributed by 29AjayKumar |
Javascript
<script> // Javascript implementation of above approach const MAX = 100; function isPossible(n, index, modulo, M, arr, dp) { // Calculate modulo for this call modulo = ((modulo % M) + M) % M; // Base case if (index == n) { // Check if sum is divisible by M if (modulo == 0) { return 1; } return 0; } // check if the current state is // already computed if (dp[index][modulo] != -1) { return dp[index][modulo]; } // 1.Try placing '+' var placeAdd = isPossible(n, index + 1, modulo + arr[index], M, arr, dp); // 2. Try placing '-' var placeMinus = isPossible(n, index + 1, modulo - arr[index], M, arr, dp); // Calculate value of res for // recursive case var res = placeAdd; // Store the value for res for current // states and return for parent call dp[index][modulo] = res; return res; } // Driver code var arr = [ 1, 2, 3, 4, 6 ]; var n = arr.length; var M = 4; // MAX is the Maximum value M can take var dp = Array(n + 1); for (i = 0; i < n + 1; i++) { dp[i] = Array(MAX).fill(-1); } var res; if (isPossible(n, 1, arr[0], M, arr, dp) == 1) { res = true ; } else { res = false ; } document.write(res ? "True" : "False" ); // This code is contributed by gauravrajput1 </script> |
True
时间复杂性: O(N*M)。
有效方法: 按照以下步骤解决问题:
- 估计 所有数组元素的模 关于给定的数字,并将其存储在新数组中,比如ModArray[]。
- 计算ModArray的和并将其存储在和中,检查和%M==0,然后输出为“真”并返回。
- 如果总和为奇数,则不存在以下情况,即无法计算为可被M整除的数字。打印“False”并返回。
- 检查总和是否为偶数,然后将其除以2,这是因为我们之前对它们进行了求和,现在的任务是删除它,因此需要删除两次,因此数字应该为偶数。
- 从ModArray中删除第一个元素,因为不能在第一个元素上加负号。
- 现在,这个解被转化为一个问题,我们要评估是否存在一个解,使得ModArray元素的和等于和或不等于和。
以下是上述方法的实施情况:
C++
// C++ program for the above approach #include <bits/stdc++.h> using namespace std; // Function to check if any valid // sequence is divisible by M void func( int n, int m, int A[]) { // DEclare mod array vector< int > ModArray(n); int sum = 0; // Calculate the mod array for ( int i = 0; i < n; i++) { ModArray[i] = A[i] % m; sum += ModArray[i]; } sum = sum % m; // Check if sum is divisible by M if (sum % m == 0) { cout << "True" ; return ; } // Check if sum is not divisible by 2 if (sum % 2 != 0) { cout << "False" ; } else { // Remove the first element from // the ModArray since it is not // possible to place minus // on the first element ModArray.erase(ModArray.begin()); int i = 0; // Decrease the size of array int j = ModArray.size() - 1; // Sort the array sort(ModArray.begin(), ModArray.end()); sum = sum / 2; int i1, i2; // Loop until the pointer // cross each other while (i <= j) { int s = ModArray[i] + ModArray[j]; // Check if sum becomes equal if (s == sum) { i1 = i; i2 = j; cout << "True" ; break ; } // Increase and decrease // the pointer accordingly else if (s > sum) j--; else i++; } } } // Driver code int main() { int m = 2; int a[] = { 1, 3, 9 }; int n = sizeof a / sizeof a[0]; // Function call func(n, m, a); } |
JAVA
// Java program for the above approach import java.util.*; class GFG{ // Function to check if any valid // sequence is divisible by M static void func( int n, int m, int []A) { // Declare mod array Vector<Integer> ModArray = new Vector<>(); for ( int i = 0 ; i < n; i++) ModArray.add( 0 ); int sum = 0 ; // Calculate the mod array for ( int i = 0 ; i < n; i++) { ModArray.set(i, A[i] % m); sum += (( int )ModArray.get(i)); } sum = sum % m; // Check if sum is divisible by M if (sum % m == 0 ) { System.out.println( "True" ); return ; } // Check if sum is not divisible by 2 if (sum % 2 != 0 ) { System.out.println( "False" ); } else { // Remove the first element from // the ModArray since it is not // possible to place minus // on the first element ModArray.remove( 0 ); int i = 0 ; // Decrease the size of array int j = ModArray.size() - 1 ; // Sort the array Collections.sort(ModArray); sum = sum / 2 ; int i1, i2; // Loop until the pointer // cross each other while (i <= j) { int s = ( int )ModArray.get(i) + ( int )ModArray.get(j); // Check if sum becomes equal if (s == sum) { i1 = i; i2 = j; System.out.println( "True" ); break ; } // Increase and decrease // the pointer accordingly else if (s > sum) j--; else i++; } } } // Driver code public static void main(String args[]) { int m = 2 ; int []a = { 1 , 3 , 9 }; int n = a.length; // Function call func(n, m, a); } } // This code is contributed by Stream_Cipher |
Python3
# Python3 program for the above approach # Function to check if any valid # sequence is divisible by M def func(n, m, A): # DEclare mod array ModArray = [ 0 ] * n Sum = 0 # Calculate the mod array for i in range (n): ModArray[i] = A[i] % m Sum + = ModArray[i] Sum = Sum % m # Check if sum is divisible by M if ( Sum % m = = 0 ) : print ( "True" ) return # Check if sum is not divisible by 2 if ( Sum % 2 ! = 0 ) : print ( "False" ) else : # Remove the first element from # the ModArray since it is not # possible to place minus # on the first element ModArray.pop( 0 ) i = 0 # Decrease the size of array j = len (ModArray) - 1 # Sort the array ModArray.sort() Sum = Sum / / 2 # Loop until the pointer # cross each other while (i < = j) : s = ModArray[i] + ModArray[j] # Check if sum becomes equal if (s = = Sum ) : i1 = i i2 = j print ( "True" ) break # Increase and decrease # the pointer accordingly elif (s > Sum ): j - = 1 else : i + = 1 # Driver code m = 2 a = [ 1 , 3 , 9 ] n = len (a) # Function call func(n, m, a) # This code is contributed by divyeshrabadiya07 |
C#
// C# program for the above approach using System.Collections.Generic; using System; class GFG{ // Function to check if any valid // sequence is divisible by M static void func( int n, int m, int []A) { // Declare mod array List< int > ModArray = new List< int >(); for ( int i = 0; i < n; i++) ModArray.Add(0); int sum = 0; // Calculate the mod array for ( int i = 0; i < n; i++) { ModArray[i] = (A[i] % m); sum += (( int )ModArray[i]); } sum = sum % m; // Check if sum is divisible by M if (sum % m == 0) { Console.WriteLine( "True" ); return ; } // Check if sum is not divisible by 2 if (sum % 2 != 0) { Console.WriteLine( "False" ); } else { // Remove the first element from // the ModArray since it is not // possible to place minus // on the first element ModArray.Remove(0); int i = 0; // Decrease the size of array int j = ModArray.Count - 1; // Sort the array ModArray.Sort(); sum = sum / 2; int i1, i2; // Loop until the pointer // cross each other while (i <= j) { int s = ( int )ModArray[i] + ( int )ModArray[j]; // Check if sum becomes equal if (s == sum) { i1 = i; i2 = j; Console.WriteLine( "True" ); break ; } // Increase and decrease // the pointer accordingly else if (s > sum) j--; else i++; } } } // Driver code public static void Main() { int m = 2; int []a = { 1, 3, 9 }; int n = a.Length; // Function call func(n, m, a); } } // This code is contributed by Stream_Cipher |
Javascript
<script> // Javascript program for the above approach // Function to check if any valid // sequence is divisible by M function func(n, m, A) { // Declare mod array let ModArray = []; for (let i = 0; i < n; i++) ModArray.push(0); let sum = 0; // Calculate the mod array for (let i = 0; i < n; i++) { ModArray[i] = A[i] % m; sum += ModArray[i]; } sum = sum % m; // Check if sum is divisible by M if (sum % m == 0) { document.write( "True" ); return ; } // Check if sum is not divisible by 2 if (sum % 2 != 0) { document.write( "False" ); } else { // Remove the first element from // the ModArray since it is not // possible to place minus // on the first element ModArray.shift(); let i = 0; // Decrease the size of array let j = ModArray.length - 1; // Sort the array ModArray.sort( function (a, b){ return a - b}); sum = parseInt(sum / 2, 10); let i1, i2; // Loop until the pointer // cross each other while (i <= j) { let s = ModArray[i] + ModArray[j]; // Check if sum becomes equal if (s == sum) { i1 = i; i2 = j; document.write( "True" ); break ; } // Increase and decrease // the pointer accordingly else if (s > sum) j--; else i++; } } } let m = 2; let a = [ 1, 3, 9 ]; let n = a.length; // Function call func(n, m, a); </script> |
False
时间复杂性: O(n*logn)


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



