价值 ![]() 精确到小数点后三位(假设
精确到小数点后三位(假设 ![]() )是。
)是。
null
注—— 这是数字型问题。 (A) 0.289 (B) 0.389 (C) 0.829 (D) 0.428 答复: (A) 说明: ![]() =
= ![]()
让X 2. =t 2倍。dx=dt dx= ![]() 限制:
限制:
x=0, ![]() t=0,
t=0, ![]()
![]()
自(π/4) 2. = 0.616
![Rendered by QuickLaTeX.com left [frac{sin{(pi / 4)}^2}{2} - frac{sin 0}{2}
ight ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cea9eab58ca545e3806cb106160dcb00_l3.png)
= ![]() = 0.289 这个问题的小测验
= 0.289 这个问题的小测验
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END
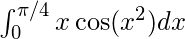


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



