关于高度平衡/AVL树的练习题

AVL树是一种二叉搜索树，其附加属性是任意节点的左子树和右子树的高度差不能大于1。以下是关于 平衡二叉树 :

• 如果AVL树中有n个节点，则AVL树的最小高度为楼层（对数） _2. n） 。
• 如果AVL树中有n个节点，最大高度不能超过1.44*log _2. N
• 如果AVL树的高度为h，则最大节点数可以为2 ^h+1 – 1.
• 高度为h的树中的最小节点数可以表示为： N（h）=N（h-1）+N（h-2）+1表示N>2，其中N（0）=1，N（1）=2。
• AVL树中搜索、插入和删除的复杂度为O（logn）。

我们讨论了基于AVL树的问题类型。

类型1：节点数和AVL树高度之间的关系- 给定节点数，问题可以被要求找到AVL树的最小和最大高度。此外，给定高度，可以询问节点的最大或最小数量。

Que–1。 任何有7个节点的AVL树的最大高度是多少？假设具有单个节点的树的高度为0。 （A） 二, （B） 三, （C） 四, （D） 五,

解决方案： 为了找到最大高度，每个级别的节点都应该是最小的。假设 高度为2，所需的最小节点数： N（h）=N（h-1）+N（h-2）+1 N（2）=N（1）+N（0）+1=2+1+1=4。 这意味着，高度2是使用最少4个节点实现的。

假设高度为3，所需的最小节点数： N（h）=N（h-1）+N（h-2）+1 N（3）=N（2）+N（1）+1=4+2+1=7。 这意味着，高度3是使用最少7个节点实现的。

因此，使用7个节点，我们可以实现最大高度为3。下面是AVL树，有7个节点，高度为3。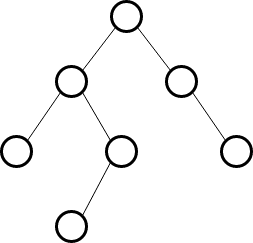

Que–2。 AVL树在最坏情况下的可能高度是多少？ （A） 2*logn （B） 1.44*logn （C） 取决于实施 （D） θ（n）

解决方案： n个节点的AVL树的最坏可能高度为1.44*logn。这可以使用具有7个节点和最大高度的AVL树进行验证。

检查选项（A），2*log7=5.6，但树的高度为3。 检查选项（B），1.44*log7=4，接近3。 检查选项（D），n=7，但树的高度为3。 其中，选项（B）是最好的答案。

类型2：基于AVL树中插入、删除和搜索的复杂性-

Que–3。 以下哪项是正确的？ （A） 搜索AVL树的代价是θ（logn），而二叉搜索树的代价是O（n） （B） 搜索一棵AVL树的代价是θ（logn），而完整二叉树的代价是θ（nlogn） （C） 二叉搜索树的搜索代价是O（logn），而AVL树的搜索代价是θ（n） （D） 搜索AVL树的代价是θ（n logn），而二叉搜索树的代价是O（n）

解决方案： AVL树的搜索、插入和删除的时间复杂度=O（logn）。但二叉搜索树可能是斜树，所以在最坏的情况下，BST搜索、插入和删除的复杂度=O（n）。

Que–4。 在具有n*2^n个元素的二元搜索树中，在平衡搜索中搜索元素的最坏情况下运行时间为

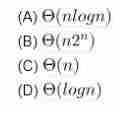
解决方案： 搜索元素所需的时间为Θ（logn），其中n是AVL树中的元素数。 由于给定的元素数为n*2^n，搜索复杂度将为Θ（log（n*2^n）），可以写成：

= Θ(log(n*2^n))
= Θ(log(n)) + Θ(log(2^n))
= Θ(log(n)) + Θ(nlog(2))
= Θ(log(n)) + Θ(n)

由于logn渐近地小于n，所以Θ（log（n））+Θ（n）可以写成与选项C匹配的Θ（n）。

类型3：在AVL树中插入和删除- 当从AVL树中插入或删除密钥时，可以在结果树上询问该问题。如果平衡系数受到干扰，则需要进行适当的旋转。

Que–5。 考虑下面的AVL树。 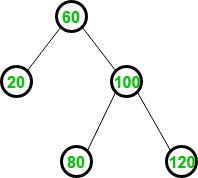以下哪项是插入70后更新的AVL树？

（A）

（B）

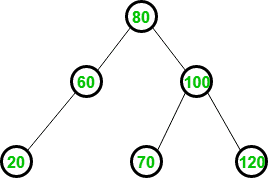（C）

（D） 没有

解决方案： 元素首先以与BST相同的方式插入。因此，插入70后，BST可以显示为：

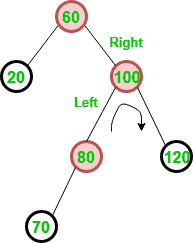
然而，平衡因子受到干扰，需要RL旋转。要移除RL旋转，首先将其转换为RR旋转，如下所示： 删除RR旋转后，生成的AVL树与选项（C）相同。