字符串所有排列的时间复杂性

打印字符串的所有排列的时间复杂性。

1. void perm(String str){
2.    perm(str, "");
3.  }
4.
5. void perm(String str, String prefix){
6.     if(str.length() == 0){
7.         System.out.println(prefix);
8.     } else{
9.        for(int i = 0; i < str.length(); i++){
10.           String rem = str.substring(0, i) + 
                           str.substring(i + 1);
11.           perm(rem, prefix + str.charAt(i));
12.       }
13.    }
14. }

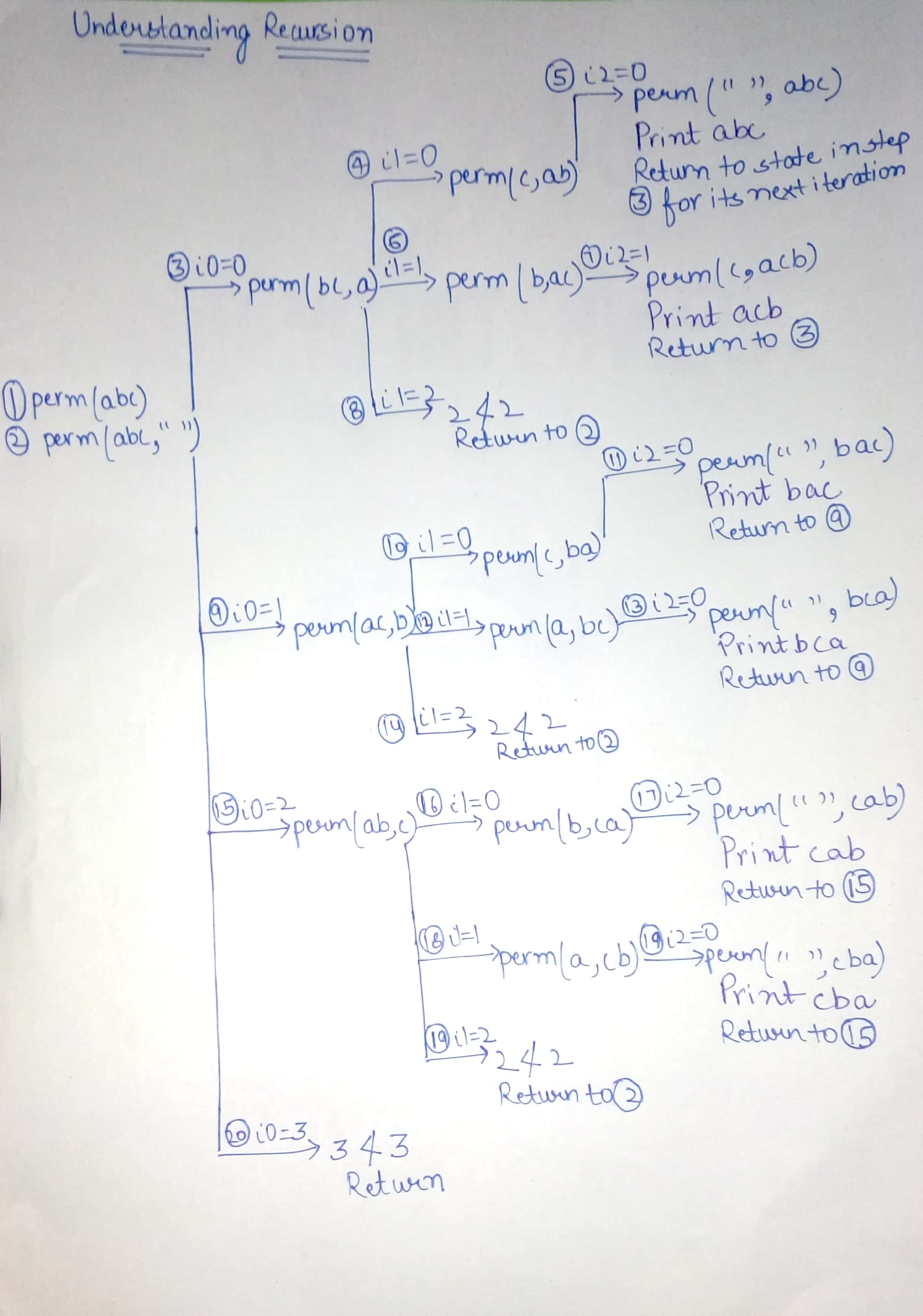
理解代码：

第1-3行： 什么时候调用函数 烫发 经过 “abc” 作为字符串参数，对perm（str，“”）进行内部调用。这意味着它从一个空前缀（第二个参数）开始，为整个字符串（第一个参数）创建置换。

第6-8行： 这是停止递归的基本情况。如果输入字符串中没有剩余的字符需要排列，则打印变量中保留的当前排列 前缀 然后回来。

第9-12行： for循环一次从输入字符串中选取一个字符来更新前缀字符串。也就是说，loop使用更新的前缀和另一个字符串再次调用函数perm 雷姆 它收集输入字符串的剩余字符。

通过以下图片了解这一点：

分析时间复杂性：

1.函数perm在其基本情况下被调用了多少次？ 我们可以从上面解释的递归中理解，对于长度为3的字符串，它打印的是6个置换，实际上是3！。这是因为，如果需要生成置换，则需要为每个槽选择字符。如果我们的字符串中有3个字符，在第一个槽中有3个选择，下一个槽有2个选择（对于前面的3个选择中的每一个，即乘法和非加法），依此类推。这说明有 N 在图像中显示的基本情况下打印排列。

2.函数perm在其基本情况之前被调用了多少次？ 考虑到9到12行 N 次数。因此，不会超过（n*n！）函数调用。

3.每个函数调用需要多长时间？ 因为，字符串前缀的每个字符都需要打印，所以执行第7行需要O（n）时间。由于字符串连接，第10行和第11行也需要O（n）时间组合，因为rem、prefix和str.charAt（i）的总和将始终为n。因此，每个函数调用对应于O（n）功。

4.总运行时间是多少？ 正在调用perm O（n*n！）次（作为上限），每次调用需要O（n）个时间，总运行时间不会超过 O（n^2*n！） .

资料来源： 破解Gayle Laakmann McDowell的编码采访