ANN学习对训练数据中的错误具有鲁棒性,并已成功应用于学习实值、离散值和向量值函数,这些函数包含诸如解释视觉场景、语音识别和学习机器人控制策略等问题。人工神经网络(ANN)的研究部分受到以下观察的启发:生物学习系统是由大脑中相互连接的神经元组成的非常复杂的网络构成的。人脑包含一个由大约10^11-10^12个神经元组成的紧密连接的网络,每个神经元平均连接到10^4-10^5个其他神经元。因此,人类大脑平均需要大约10^-1才能做出令人惊讶的复杂决定。人工神经网络系统的动机是捕捉这种基于分布式表示的高度并行计算。一般来说,人工神经网络是由一组紧密相连的简单单元构成的,其中每个单元接受多个实值输入,并产生单个实值输出。 但是人工神经网络不太受生物神经系统的驱动,生物神经系统有许多不由人工神经网络建模的复杂性。其中一些如图所示。
生物神经元与人工神经元的区别
| 生物神经元 | 人工神经元 |
|---|---|
| 主要成分:轴子、树突、突触 | 主要成分:节点、输入、输出、权重、偏差 |
| 来自其他神经元的信息以电脉冲的形式进入树突的突触连接点。信息从树突流向细胞进行处理。输出信号是一系列脉冲,然后通过轴突传递到其他神经元的突触。 | 神经元的排列和连接构成了这个网络,有三层。第一层称为输入层,是唯一暴露于外部信号的层。输入层将信号传输给下一层的神经元,这一层被称为隐藏层。隐藏层从接收到的信号中提取相关特征或图案。这些被认为重要的特征或模式随后被引导到输出层,这是网络的最后一层。 |
| 突触可以增加或减少连接的强度。这是存储信息的地方。 | 人工信号可以通过权重改变,其方式类似于突触中发生的物理变化。 |
| 大约10 11 神经元。 | 10 2. – 10 4. 使用当前技术的神经元 |
人脑和计算机在信息处理方式上的差异。
| 人脑(生物神经元网络) | 计算机(人工神经元网络) |
|---|---|
| 人脑是异步工作的 | 计算机(ANN)同步工作。 |
| 生物神经元计算速度慢(每次计算几毫秒) | 人工神经元计算速度快(每次计算小于1纳秒) |
| 大脑以分布式方式表示信息,因为神经元不可靠,随时可能死亡。 | 在计算机程序中,每一位都必须按预期运行,否则这些程序就会崩溃。 |
| 随着时间的推移,我们的大脑会改变它们的连通性,以代表强加给我们的新信息和要求。 | 除非我们更换电脑部件,否则电脑电子部件之间的连接永远不会改变。 |
| 生物神经网络具有复杂的拓扑结构。 | 人工神经网络通常是树形结构。 |
| 研究人员仍在探索大脑究竟是如何学习的。 | 人工神经网络使用梯度下降进行学习。 |
使用人工神经网络的优势:
- ANN中的问题可能有由许多属性值对表示的实例。
- 用于具有目标函数输出的问题的ANN可以是离散值、实值或多个实值或离散值属性的向量。
- 神经网络学习方法对训练数据中的噪声具有很强的鲁棒性。培训示例可能包含错误,这些错误不会影响最终输出。
- 它通常用于可能需要快速评估学习目标函数的地方。
- ANN可以承受较长的训练时间,这取决于网络中权重的数量、考虑的训练示例的数量以及各种学习算法参数的设置等因素。
McCulloch-Pitts神经元模型: 人工神经元的早期模型由 沃伦·麦卡洛克 1943年的沃尔特·皮特。McCulloch-Pitts神经模型也称为线性阈值门。它是一组输入I1、I2、…、Im和一个输出y的神经元。线性阈值门将输入集简单地划分为两类。因此,输出y是二进制的。这样的函数可以用以下方程式进行数学描述:

W1,W2,W3…。Wn是在(0,1)或(-1,1)范围内标准化的权重值,与每个输入行关联,Sum是加权和,是阈值常数。函数f是阈值处的线性阶跃函数
单层神经网络(感知器) 输入是多维的(即输入可以是向量): 输入x=(I1,I2,…,In) 输入节点(或单元)与下一层中的一个节点(或多个节点)连接(通常完全连接)。下一层中的节点获取其所有输入的加权和: ![]()
规则是: 输出节点有一个“阈值”t。 规则:如果输入相加?t、 然后它“启动”(输出y=1)。否则(总输入 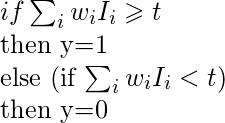 哪一个
哪一个 ![图片[4]-人工神经网络简介|集1-yiteyi-C++库](https://media.geeksforgeeks.org/wp-content/uploads/booleanfunctions.jpg)
感知机的局限性: (i) 由于硬极限传递函数,感知器的输出值只能采用两个值(0或1)中的一个。 (ii)感知器只能对线性可分离的向量集进行分类。如果可以画一条直线或一个平面将输入向量分成正确的类别,则输入向量是线性可分的。如果向量不是线性可分的,学习将永远不会达到所有向量都被正确分类的程度 布尔函数XOR不是线性可分的(其正实例和负实例不能用直线或超平面分隔)。因此,单层感知器永远无法计算异或函数。这是曾经导致神经网络领域停滞的一大缺陷。但这一问题已通过多层膜技术解决。
多层神经网络 多层感知器(MLP)或多层神经网络包含一个或多个隐藏层(除了一个输入层和一个输出层)。单层感知器只能学习线性函数,而多层感知器也可以学习非线性函数。
![图片[5]-人工神经网络简介|集1-yiteyi-C++库](https://media.geeksforgeeks.org/wp-content/uploads/nodeNeural.jpg)
这个神经元把x1,x2,…。,x3(和a+1偏差项)和输出f(总输入+偏差),其中f(.)调用激活函数。偏差的主要功能是为每个节点提供一个可训练的常量值(除了节点接收的正常输入)。每个激活函数(或非线性)取一个数字,并对其执行特定的固定数学运算。在实践中,您可能会遇到几种激活功能:
乙状结肠: 接受实值输入并将其压缩到0到1之间。 ![]() 谭: 获取实值输入并将其压缩到范围[-1,1]。
谭: 获取实值输入并将其压缩到范围[-1,1]。 ![]() 雷卢: ReLu代表校正后的线性单位。它接受实值输入并将其阈值设置为0(将负值替换为0)。
雷卢: ReLu代表校正后的线性单位。它接受实值输入并将其阈值设置为0(将负值替换为0)。 ![]()
参考资料:
- Christos Stergiou和Dimitrios Siganos的神经网络
- ujjwalkarn。我
- 机器学习,汤姆·米切尔,麦格劳·希尔,1997年。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



