节点数与二叉树高度的关系

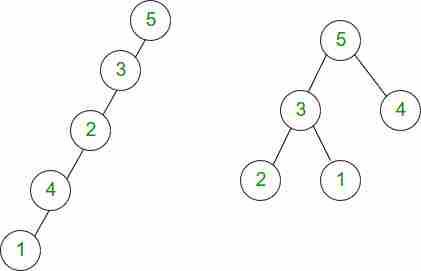
先决条件—— 二叉树数据结构 在本文中，我们将讨论节点数和二叉树高度之间关系的各种情况。在理解本文之前，您应该对二叉树及其属性有基本的了解。 这个 身高 二叉树的最长路径是从根开始的 任何叶子的节点 树中的节点。例如，图1（b）所示的二叉树的高度是2，因为从根节点到节点2的最长路径是2。此外，图1（a）所示的二叉树的高度是4。

二叉树- 在二叉树中，一个节点最多可以有两个子节点。

根据节点数计算最小和最大高度—— 如果二叉树中有n个节点， 最大高度 二叉树的 n-1 和 最小高度 是 楼层（log2n） .

例如，图1（a）所示的有5个节点的左偏二叉树的高度为5-1=4，图1（b）所示的有5个节点的二叉树的高度为2。

从高度计算最小和最大节点数—— 如果二叉树 高度h ，最少 节点数为h+1 （对于左偏和右偏二叉树）。

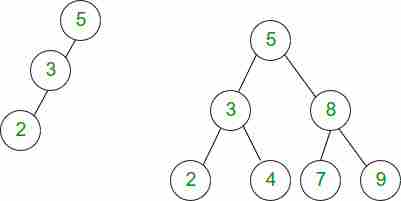
例如，图2（a）中高度为2的二叉树有3个节点。 如果二叉树的高度为h，则当所有级别都已满时，节点的最大数量将为。节点总数将为2^0+2^1+…。2^h=2^（h+1）-1。 例如，图2（b）中高度为2的二叉树有2^（2+1）-1=7个节点。

二叉搜索树– 在二元搜索树中，节点的左子节点的值小于父节点，右子节点的值大于父节点。

根据节点数计算最小和最大高度—— 如果二叉搜索树中有n个节点，则二叉搜索树的最大高度为n-1，最小高度为ceil（log2n）。

从高度计算最小和最大节点数—— 如果二叉搜索树 高度h ，最少 节点数为h+1 （对于左偏和右偏二叉搜索树）。 如果二叉搜索树 高度h ，当所有级别都已满时，节点的最大数量将为。节点总数将为2^0+2^1+…。2^h=2^（h+1）-1。

BST中的所有规则都与二叉树中的规则相同，并且可以以相同的方式进行可视化。

Que-1。 树的高度是其中最长的根到叶的路径的长度。高度为5的二叉树中的最大和最小节点数为： （A） 分别为63和6 （B） 分别为64和5 （C） 分别为32和6 （D） 分别为31和5

解决方案： 根据讨论的公式， 最大节点数=2^（h+1）-1=2^6-1=63。 最小节点数=h+1=5+1=6。

奎-2。 对于一个有50个节点的二叉树，下列哪个高度是不可能的？ （A） 四, （B） 五, （C） 六, （D） 没有

解决方案： 根据讨论的公式， 50个节点的最小高度=楼层（log250）=5。因此，高度4是不可能的。