Tango树数据结构

探戈树是一种 在线算法 .这是一种二进制搜索树。它比 离线权重平衡二叉搜索树 当它达到 竞争比率 属于 与竞争对手相比 离线权重平衡二叉搜索树。只要 在树的每个节点上增加额外的内存位，以提高权重平衡二叉搜索树的性能。 Tango树在概念上是一棵树的树，因为它将二叉搜索树划分为 首选路径 和 非首选路径 还有这些 首选路径 它们本身以辅助树的形式存储。

首选子级和首选路径 Tango树的任何节点的首选子节点被定义为通过常规二叉搜索树查找技术最近接触的子节点。关于首选子节点的详细说明，让我们假设一个子树T以节点n为根，右子节点为p，左子节点为q。如果最近访问的以n为根的子树节点位于以p为根的子树中，则称p为n的首选子节点。 A. 首选路径 定义为从根节点开始，沿着路径跟随所有首选子节点到达叶节点的路径。

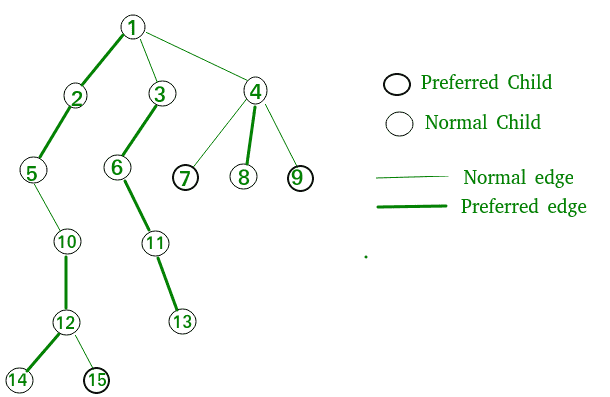
探戈树

优先路径的辅助树 首选路径通过将首选路径的节点存储在平衡二叉搜索树（特别是红黑树）中来表示。然后，对于路径P的每个非叶节点，都有一个非首选子节点 。此非首选子级充当新辅助树的根，然后将此新辅助树附加到根 通过这种方式，很容易将辅助树连接在一起。还可以根据我们自己的需要，在辅助树的每个节点中存储一些额外的信息，比如它下面的子树中节点的最小深度，等等。

探戈树上的行动 探戈树上最常见的两种操作是 搜索 和 更新

• 在探戈树中更新

  它需要维护Tango树的结构，因为每次搜索后，节点的首选子节点都会发生变化，因此需要不断更新。每当首选路径发生变化时，首选路径将在发生变化的特定节点上分为两部分，首选路径的顶部需要连接到另一个首选路径的末端。为此，将更新分为两部分：

  1. 切割过程

     在该操作中，在给定节点处将首选路径分为两条路径——顶部和底部。顶部是包含某个节点级别以上节点的辅助树，底部是包含给定节点级别以下节点的辅助树。

  2. 加入过程

     在这个操作中，我们将两个辅助树组合在一起。但是，只有当其中一个合并树的底部节点是另一个合并树的顶部节点的父节点时，才能合并它们。此联接操作使用 红黑树 .在顶部路径中存在两个节点，因此，如果在这两个节点之间存在its键值，则称节点位于底部路径中。为了连接，我们只需在这两个节点之间拆分顶部路径，然后将两个生成的辅助树连接到底部路径，生成的辅助树就准备好了。

• 在探戈树上寻找

  要在探戈树中搜索，我们只需在概念二叉搜索树中执行搜索。首先通过搜索其辅助树来搜索首选路径。如果在给定的辅助树中找不到节点，则搜索下一条路径的辅助树，依此类推，直到搜索整个树或找不到所需的节点。