给定一个正整数 N .任务是求二项系数的平方和,即 N C 0 2. + N C 1. 2. + N C 2. 2. + N C 3. 2. + ……… + N C n-2 2. + N C n-1 2. + N C N 2. 例如:
null
Input : n = 4Output : 70Input : n = 5Output : 252
方法1:(暴力) 其思想是生成二项式系数的所有项,并求每个二项式系数的平方和。 以下是该方法的实施情况:
C++
// CPP Program to find the sum of square of // binomial coefficient. #include<bits/stdc++.h> using namespace std; // Return the sum of square of binomial coefficient int sumofsquare( int n) { int C[n+1][n+1]; int i, j; // Calculate value of Binomial Coefficient // in bottom up manner for (i = 0; i <= n; i++) { for (j = 0; j <= min(i, n); j++) { // Base Cases if (j == 0 || j == i) C[i][j] = 1; // Calculate value using previously // stored values else C[i][j] = C[i-1][j-1] + C[i-1][j]; } } // Finding the sum of square of binomial // coefficient. int sum = 0; for ( int i = 0; i <= n; i++) sum += (C[n][i] * C[n][i]); return sum; } // Driven Program int main() { int n = 4; cout << sumofsquare(n) << endl; return 0; } |
JAVA
// Java Program to find the sum of // square of binomial coefficient. import static java.lang.Math.*; class GFG{ // Return the sum of square of // binomial coefficient static int sumofsquare( int n) { int [][] C = new int [n+ 1 ][n+ 1 ] ; int i, j; // Calculate value of Binomial // Coefficient in bottom up manner for (i = 0 ; i <= n; i++) { for (j = 0 ; j <= min(i, n); j++) { // Base Cases if (j == 0 || j == i) C[i][j] = 1 ; // Calculate value using //previously stored values else C[i][j] = C[i- 1 ][j- 1 ] + C[i- 1 ][j]; } } // Finding the sum of square of // binomial coefficient. int sum = 0 ; for (i = 0 ; i <= n; i++) sum += (C[n][i] * C[n][i]); return sum; } // Driver function public static void main(String[] args) { int n = 4 ; System.out.println(sumofsquare(n)); } } // This code is contributed by // Smitha Dinesh Semwal |
Python3
# Python Program to find # the sum of square of # binomial coefficient. # Return the sum of # square of binomial # coefficient def sumofsquare(n) : C = [[ 0 for i in range (n + 1 )] for j in range (n + 1 )] # Calculate value of # Binomial Coefficient # in bottom up manner for i in range ( 0 , n + 1 ) : for j in range ( 0 , min (i, n) + 1 ) : # Base Cases if (j = = 0 or j = = i) : C[i][j] = 1 # Calculate value # using previously # stored values else : C[i][j] = (C[i - 1 ][j - 1 ] + C[i - 1 ][j]) # Finding the sum of # square of binomial # coefficient. sum = 0 for i in range ( 0 , n + 1 ) : sum = sum + (C[n][i] * C[n][i]) return sum # Driver Code n = 4 print (sumofsquare(n), end = "" ) # This code is contributed by # Manish Shaw(manishshaw1) |
C#
// C# Program to find the sum of // square of binomial coefficient. using System; class GFG { // Return the sum of square of // binomial coefficient static int sumofsquare( int n) { int [,] C = new int [n+1,n+1] ; int i, j; // Calculate value of Binomial // Coefficient in bottom up manner for (i = 0; i <= n; i++) { for (j = 0; j <= Math.Min(i, n); j++) { // Base Cases if (j == 0 || j == i) C[i,j] = 1; // Calculate value using //previously stored values else C[i,j] = C[i-1,j-1] + C[i-1,j]; } } // Finding the sum of square of // binomial coefficient. int sum = 0; for (i = 0; i <= n; i++) sum += (C[n,i] * C[n,i]); return sum; } // Driver function public static void Main() { int n = 4; Console.WriteLine(sumofsquare(n)); } } // This code is contributed by vt_m. |
PHP
<?php // PHP Program to find the sum of // square of binomial coefficient. // Return the sum of square of binomial // coefficient function sumofsquare( $n ) { $i ; $j ; // Calculate value of Binomial // Coefficient in bottom up manner for ( $i = 0; $i <= $n ; $i ++) { for ( $j = 0; $j <= min( $i , $n ); $j ++) { // Base Cases if ( $j == 0 || $j == $i ) $C [ $i ][ $j ] = 1; // Calculate value using previously // stored values else $C [ $i ][ $j ] = $C [ $i -1][ $j -1] + $C [ $i -1][ $j ]; } } // Finding the sum of square of binomial // coefficient. $sum = 0; for ( $i = 0; $i <= $n ; $i ++) $sum += ( $C [ $n ][ $i ] * $C [ $n ][ $i ]); return $sum ; } // Driven Program $n = 4; echo sumofsquare( $n ), "" ; // This code is contributed by ajit ?> |
Javascript
<script> // JavaScript Program to find the sum of // square of binomial coefficient. // Return the sum of square of // binomial coefficient function sumofsquare(n) { let C = new Array(n+1); // Loop to create 2D array using 1D array for (let i = 0; i < C.length; i++) { C[i] = new Array(2); } let i, j; // Calculate value of Binomial // Coefficient in bottom up manner for (i = 0; i <= n; i++) { for (j = 0; j <= Math.min(i, n); j++) { // Base Cases if (j == 0 || j == i) C[i][j] = 1; // Calculate value using //previously stored values else C[i][j] = C[i-1][j-1] + C[i-1][j]; } } // Finding the sum of square of // binomial coefficient. let sum = 0; for (i = 0; i <= n; i++) sum += (C[n][i] * C[n][i]); return sum; } // Driver code let n = 4; document.write(sumofsquare(n)); // This code is contributed by code_hunt. </script> |
输出:
70
方法2:(使用公式) ![]() =
= ![]() =
= ![]() 证据
证据
We know,(1 + x)n = nC0 + nC1 x + nC2 x2 + ......... + nCn-1 xn-1 + nCn-1 xnAlso,(x + 1)n = nC0 xn + nC1 xn-1 + nC2 xn-2 + ......... + nCn-1 x + nCnMultiplying above two equations,(1 + x)2n = [nC0 + nC1 x + nC2 x2 + ......... + nCn-1 xn-1 + nCn-1 xn] X [nC0 xn + nC1 xn-1 + nC2 xn-2 + ......... + nCn-1 x + nCn]Equating coefficients of xn on both sides, we get2nCn = nC02 + nC12 + nC22 + nC32 + ......... + nCn-22 + nCn-12 + nCn2Hence, sum of the squares of coefficients = 2nCn = (2n)!/(n!)2.
还有,(2n)/(n!) 2. =(2n*(2n-1)*(2n-2)*……*(n+1))/(n*(n-1)*(n-2)*……*1). 以下是该方法的实施情况:
C++
// CPP Program to find the sum of square of // binomial coefficient. #include<bits/stdc++.h> using namespace std; // function to return product of number // from start to end. int factorial( int start, int end) { int res = 1; for ( int i = start; i <= end; i++) res *= i; return res; } // Return the sum of square of binomial // coefficient int sumofsquare( int n) { return factorial(n+1, 2*n)/factorial(1, n); } // Driven Program int main() { int n = 4; cout << sumofsquare(n) << endl; return 0; } |
JAVA
// Java Program to find the sum of square of // binomial coefficient. class GFG{ // function to return product of number // from start to end. static int factorial( int start, int end) { int res = 1 ; for ( int i = start; i <= end; i++) res *= i; return res; } // Return the sum of square of binomial // coefficient static int sumofsquare( int n) { return factorial(n+ 1 , 2 *n)/factorial( 1 , n); } // Driven Program public static void main(String[] args) { int n = 4 ; System.out.println(sumofsquare(n)); } } // This code is contributed by // Smitha DInesh Semwal |
python
# Python 3 Program to find the sum of # square of binomial coefficient. # function to return product of number # from start to end. def factorial(start, end): res = 1 for i in range (start, end + 1 ): res * = i return res # Return the sum of square of binomial # coefficient def sumofsquare(n): return int (factorial(n + 1 , 2 * n) / factorial( 1 , n)) # Driven Program n = 4 print (sumofsquare(n)) # This code is contributed by # Smitha Dinesh Semwal |
C#
// C# Program to find the sum of square of // binomial coefficient. using System; class GFG { // function to return product of number // from start to end. static int factorial( int start, int end) { int res = 1; for ( int i = start; i <= end; i++) res *= i; return res; } // Return the sum of square of binomial // coefficient static int sumofsquare( int n) { return factorial(n+1, 2*n)/factorial(1, n); } // Driven Program public static void Main() { int n = 4; Console.WriteLine(sumofsquare(n)); } } // This code is contributed by vt_m. |
PHP
<?php // PHP Program to find the sum // of square of binomial coefficient. // function to return // product of number // from start to end. function factorial( $start , $end ) { $res = 1; for ( $i = $start ; $i <= $end ; $i ++) $res *= $i ; return $res ; } // Return the sum of // square of binomial // coefficient function sumofsquare( $n ) { return factorial( $n + 1, 2 * $n ) / factorial(1, $n ); } // Driver Code $n = 4; echo sumofsquare( $n ), "" ; // This code is contributed by ajit ?> |
Javascript
<script> // Javascript Program to find // the sum of square of // binomial coefficient. // function to return product of number // from start to end. function factorial(start, end) { let res = 1; for (let i = start; i <= end; i++) res *= i; return res; } // Return the sum of square of binomial // coefficient function sumofsquare(n) { return parseInt (factorial(n+1, 2*n)/factorial(1, n), 10); } let n = 4; document.write(sumofsquare(n)); </script> |
输出:
70
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END
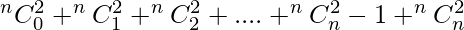


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



