我们必须画n块长度为{A1，A2，…An}的木板。有k个油漆工可用，每个油漆工需要1个单位的时间来油漆1个单位的木板。问题是，在任何油漆工只会绘制连续的电路板部分的约束条件下，找到完成这项工作的最短时间，比如电路板{2,3,4}，或者只绘制电路板{1}，或者只绘制电路板{2,4,5}，什么都不绘制。
null
例如：
Input : k = 2, A = {10, 10, 10, 10} Output : 20.Here we can divide the boards into 2equal sized partitions, so each painter gets 20 units of board and the totaltime taken is 20. Input : k = 2, A = {10, 20, 30, 40} Output : 60.Here we can divide first 3 boards forone painter and the last board for second painter.
在 以前的职位 我们讨论了一种基于动态规划的方法，其时间复杂度为 
和 
额外的空间。 在本文中，我们将探讨一种更有效的使用二进制搜索的方法。我们知道二进制搜索的不变量有两个主要部分： *目标值将始终在搜索范围内。 *搜索范围将在每个循环中减小，以便可以达到终止。
我们还知道，这个范围内的值必须按顺序排序。在这里，我们的目标值是电路板最佳分配中相邻部分的最大和。现在我们如何应用二进制搜索呢？我们可以确定目标值的可能从低到高的范围，并缩小搜索范围以获得最佳分配。
我们可以看到，在这个范围内，最大的可能值是数组中所有元素的总和，当我们为电路板的所有部分分配1个painter时，就会出现这种情况。这个范围的最低可能值是席max的最大值，因为在这个分配中，我们可以分配最大值给一个画家，并且分割其他部分，例如它们的成本小于或等于max，并且尽可能接近max。现在，如果我们考虑在上面的场景中使用X画家，那么显然，随着范围内的值增加，x的值减小，反之亦然。由此我们可以找到x=k时的目标值，并使用辅助函数来找到x，即给定画家可以绘制的最大截面长度时所需的最小画家人数。
C++
// CPP program for painter's partition problem #include <iostream> #include <climits> using namespace std; // return the maximum element from the array int getMax( int arr[], int n) { int max = INT_MIN; for ( int i = 0; i < n; i++) if (arr[i] > max) max = arr[i]; return max; } // return the sum of the elements in the array int getSum( int arr[], int n) { int total = 0; for ( int i = 0; i < n; i++) total += arr[i]; return total; } // find minimum required painters for given maxlen // which is the maximum length a painter can paint int numberOfPainters( int arr[], int n, int maxLen) { int total = 0, numPainters = 1; for ( int i = 0; i < n; i++) { total += arr[i]; if (total > maxLen) { // for next count total = arr[i]; numPainters++; } } return numPainters; } int partition( int arr[], int n, int k) { int lo = getMax(arr, n); int hi = getSum(arr, n); while (lo < hi) { int mid = lo + (hi - lo) / 2; int requiredPainters = numberOfPainters(arr, n, mid); // find better optimum in lower half // here mid is included because we // may not get anything better if (requiredPainters <= k) hi = mid; // find better optimum in upper half // here mid is excluded because it gives // required Painters > k, which is invalid else lo = mid + 1; } // required return lo; } // driver function int main() { int arr[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }; int n = sizeof (arr) / sizeof (arr[0]); int k = 3; cout << partition(arr, n, k) << endl; return 0; } |
JAVA
// Java Program for painter's partition problem import java.util.*; import java.io.*; class GFG { // return the maximum element from the array static int getMax( int arr[], int n) { int max = Integer.MIN_VALUE; for ( int i = 0 ; i < n; i++) if (arr[i] > max) max = arr[i]; return max; } // return the sum of the elements in the array static int getSum( int arr[], int n) { int total = 0 ; for ( int i = 0 ; i < n; i++) total += arr[i]; return total; } // find minimum required painters for given maxlen // which is the maximum length a painter can paint static int numberOfPainters( int arr[], int n, int maxLen) { int total = 0 , numPainters = 1 ; for ( int i = 0 ; i < n; i++) { total += arr[i]; if (total > maxLen) { // for next count total = arr[i]; numPainters++; } } return numPainters; } static int partition( int arr[], int n, int k) { int lo = getMax(arr, n); int hi = getSum(arr, n); while (lo < hi) { int mid = lo + (hi - lo) / 2 ; int requiredPainters = numberOfPainters(arr, n, mid); // find better optimum in lower half // here mid is included because we // may not get anything better if (requiredPainters <= k) hi = mid; // find better optimum in upper half // here mid is excluded because it gives // required Painters > k, which is invalid else lo = mid + 1 ; } // required return lo; } // Driver code public static void main(String args[]) { int arr[] = { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 }; // Calculate size of array. int n = arr.length; int k = 3 ; System.out.println(partition(arr, n, k)); } } // This code is contributed by Sahil_Bansall |
Python3
# Python program for painter's partition problem # Find minimum required painters for given maxlen # which is the maximum length a painter can paint def numberOfPainters(arr, n, maxLen): total = 0 numPainters = 1 for i in arr: total + = i if (total > maxLen): # for next count total = i numPainters + = 1 return numPainters def partition(arr, n, k): lo = max (arr) hi = sum (arr) while (lo < hi): mid = lo + (hi - lo) / / 2 requiredPainters = numberOfPainters(arr, n, mid) # find better optimum in lower half # here mid is included because we # may not get anything better if (requiredPainters < = k): hi = mid # find better optimum in upper half # here mid is excluded because it gives # required Painters > k, which is invalid else : lo = mid + 1 # required return lo # Driver code arr = [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 ] n = len (arr) k = 3 print ( int (partition(arr, n, k))) |
C#
// C# Program for painter's // partition problem using System; class GFG { // return the maximum // element from the array static int getMax( int [] arr, int n) { int max = int .MinValue; for ( int i = 0; i < n; i++) if (arr[i] > max) max = arr[i]; return max; } // return the sum of the // elements in the array static int getSum( int [] arr, int n) { int total = 0; for ( int i = 0; i < n; i++) total += arr[i]; return total; } // find minimum required // painters for given // maxlen which is the // maximum length a painter // can paint static int numberOfPainters( int [] arr, int n, int maxLen) { int total = 0, numPainters = 1; for ( int i = 0; i < n; i++) { total += arr[i]; if (total > maxLen) { // for next count total = arr[i]; numPainters++; } } return numPainters; } static int partition( int [] arr, int n, int k) { int lo = getMax(arr, n); int hi = getSum(arr, n); while (lo < hi) { int mid = lo + (hi - lo) / 2; int requiredPainters = numberOfPainters(arr, n, mid); // find better optimum in lower // half here mid is included // because we may not get // anything better if (requiredPainters <= k) hi = mid; // find better optimum in upper // half here mid is excluded // because it gives required // Painters > k, which is invalid else lo = mid + 1; } // required return lo; } // Driver code static public void Main() { int [] arr = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }; // Calculate size of array. int n = arr.Length; int k = 3; Console.WriteLine(partition(arr, n, k)); } } // This code is contributed by ajit |
PHP
<?php // PHP program for painter's // partition problem // return the maximum // element from the array function getMax( $arr , $n ) { $max = PHP_INT_MIN; for ( $i = 0; $i < $n ; $i ++) if ( $arr [ $i ] > $max ) $max = $arr [ $i ]; return $max ; } // return the sum of the // elements in the array function getSum( $arr , $n ) { $total = 0; for ( $i = 0; $i < $n ; $i ++) $total += $arr [ $i ]; return $total ; } // find minimum required painters // for given maxlen which is the // maximum length a painter can paint function numberOfPainters( $arr , $n , $maxLen ) { $total = 0; $numPainters = 1; for ( $i = 0; $i < $n ; $i ++) { $total += $arr [ $i ]; if ( $total > $maxLen ) { // for next count $total = $arr [ $i ]; $numPainters ++; } } return $numPainters ; } function partition( $arr , $n , $k ) { $lo = getMax( $arr , $n ); $hi = getSum( $arr , $n ); while ( $lo < $hi ) { $mid = $lo + ( $hi - $lo ) / 2; $requiredPainters = numberOfPainters( $arr , $n , $mid ); // find better optimum in // lower half here mid is // included because we may // not get anything better if ( $requiredPainters <= $k ) $hi = $mid ; // find better optimum in // upper half here mid is // excluded because it // gives required Painters > k, // which is invalid else $lo = $mid + 1; } // required return floor ( $lo ); } // Driver Code $arr = array (1, 2, 3, 4, 5, 6, 7, 8, 9); $n = sizeof( $arr ); $k = 3; echo partition( $arr , $n , $k ), "" ; // This code is contributed by ajit ?> |
Javascript
<script> // Javascript Program for painter's partition problem // Return the maximum element from the array function getMax(arr, n) { let max = Number.MIN_VALUE; for (let i = 0; i < n; i++) if (arr[i] > max) max = arr[i]; return max; } // Return the sum of the elements in the array function getSum(arr, n) { let total = 0; for (let i = 0; i < n; i++) total += arr[i]; return total; } // Find minimum required paleters for given maxlen // which is the maximum length a paleter can palet function numberOfPaleters(arr, n, maxLen) { let total = 0, numPaleters = 1; for (let i = 0; i < n; i++) { total += arr[i]; if (total > maxLen) { // For next count total = arr[i]; numPaleters++; } } return numPaleters; } function partition(arr, n, k) { let lo = getMax(arr, n); let hi = getSum(arr, n); while (lo < hi) { let mid = lo + (hi - lo) / 2; let requiredPaleters = numberOfPaleters( arr, n, mid); // Find better optimum in lower half // here mid is included because we // may not get anything better if (requiredPaleters <= k) hi = mid; // find better optimum in upper half // here mid is excluded because it gives // required Paleters > k, which is invalid else lo = mid + 1; } // Required return lo; } // Driver code let arr = [ 1, 2, 3, 4, 5, 6, 7, 8, 9 ]; // Calculate size of array. let n = arr.length; let k = 3; document.write(Math.round(partition(arr, n, k))); // This code is contributed by sanjoy_62 </script> |
输出：
17
为了更好地理解，请用钢笔和纸追踪程序中给出的示例。 上述方法的时间复杂度为 ![O(N * log (sum (arr[]))](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-08191bd378c05fa39ddb6bf77dd05b52_l3.png "Rendered by QuickLaTeX.com")
. 参考资料： https://articles.leetcode.com/the-painters-partition-problem-part-ii/ https://www.topcoder.com/community/data-science/data-science-tutorials/binary-search/ 问：谷歌，代码国家。
© 版权声明
文章版权归作者所有，未经允许请勿转载。
THE END
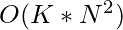
![关于”PostgreSQL错误：关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)
