给出了一个N*N矩阵,其中矩阵的每个元素都在0到M的范围内。可以对矩阵应用以下操作任意次数:
null
- 选择任意两个连续的元素
- 其中一个增加1,另一个减少1
注: 应用上述操作后,元件应保持在0到M的范围内。 如果需要,任务是在矩阵上执行上述操作后,找到下面所示表达式的最大值:
res += (i+j)*A[i][j]for 0 <= i, j <= N
例如:
Input : A[][] = {1, 2, 5, 1} M = 5Output : RESULT = 27Matrix : 0 0 4 5Input : A[][] = {3, 4, 5, 4} M = 6Output : RESULT = 43Matrix : 0 4 6 6
算法: 下面是实现这一点的分步算法:
- 首先,计算给定矩阵中所有元素的和作为和。
- 从最后一个元素开始,即A(n,n),向后移动到A(0,0)反对角线方向,如A(n,n),A(n,n-1,n),A(n,n-2),A(n-1,n-1),A(n-2,n)…。。
- 用M填充矩阵的每个单元格,并更新每个元素的SUM=SUM-M,直到SUM
- 最后你可以根据上述公式计算结果。
例子: 输入矩阵:
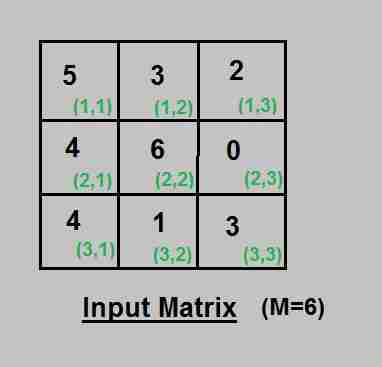
应用上述算法后的解矩阵:
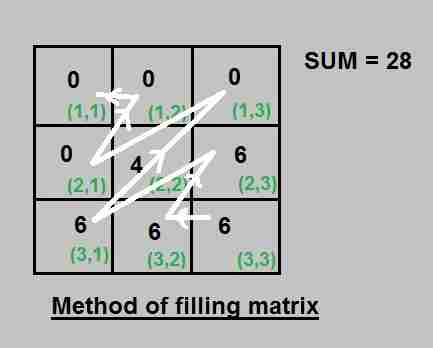
以下是上述理念的实施:
C++
// CPP to maximize matrix result #include<bits/stdc++.h> using namespace std; #define n 4 // utility function for maximize matrix result int maxMatrix( int A[][n], int M) { int sum = 0, res = 0; for ( int i=0; i<n ; i++) for ( int j=0; j<n; j++) sum += A[i][j]; // diagonals below longest diagonal // starting from last element of matrix for ( int j=n-1; j>0; j--) { for ( int i=0; i<n-j; i++) { if (sum > M) { A[n-1-i][j+i] = M; sum -= M; } else { A[n-1-i][j+i] = sum; sum -= sum; } } } // diagonals above longest diagonal for ( int i=n-1; i>=0; i--) { for ( int j=0; j<=i; j++) { if (sum > M) { A[i-j][j] = M; sum -= M; } else { A[i-j][j] = sum; sum -= sum; } } } // calculating result for ( int i=0; i<n; i++) { for ( int j=0; j<n;j++) res += (i+j+2) * A[i][j]; } return res; } // driver program int main() { int A[n][n] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 1, 2, 3, 4, 5, 6}; int m = 9; cout << maxMatrix(A, m); return 0; } |
JAVA
// Java to maximize matrix result class GFG { static final int n = 4 ; // utility function for maximize matrix result static int maxMatrix( int A[][], int M) { int sum = 0 , res = 0 ; for ( int i = 0 ; i < n; i++) { for ( int j = 0 ; j < n; j++) { sum += A[i][j]; } } // diagonals below longest diagonal // starting from last element of matrix for ( int j = n - 1 ; j > 0 ; j--) { for ( int i = 0 ; i < n - j; i++) { if (sum > M) { A[n - 1 - i][j + i] = M; sum -= M; } else { A[n - 1 - i][j + i] = sum; sum -= sum; } } } // diagonals above longest diagonal for ( int i = n - 1 ; i >= 0 ; i--) { for ( int j = 0 ; j <= i; j++) { if (sum > M) { A[i - j][j] = M; sum -= M; } else { A[i - j][j] = sum; sum -= sum; } } } // calculating result for ( int i = 0 ; i < n; i++) { for ( int j = 0 ; j < n; j++) { res += (i + j + 2 ) * A[i][j]; } } return res; } // driver program static public void main(String[] args) { int A[][] = {{ 1 , 2 , 3 , 4 }, { 5 , 6 , 7 , 8 }, { 9 , 1 , 1 , 2 }, { 3 , 4 , 5 , 6 }}; int m = 9 ; System.out.println(maxMatrix(A, m)); } } // This code is contributed by Rajput-Ji |
Python3
# Python to maximize matrix result n = 4 # utility function for maximize # matrix result def maxMatrix(A, M): sum , res = 0 , 0 for i in range (n): for j in range (n): sum + = A[i][j] # diagonals below longest diagonal # starting from last element of matrix for j in range (n - 1 , 0 , - 1 ): for i in range (n - j): if ( sum > M): A[n - 1 - i][j + i] = M sum - = M else : A[n - 1 - i][j + i] = sum sum - = sum # diagonals above longest diagonal for i in range (n - 1 , - 1 , - 1 ): for j in range (i + 1 ): if ( sum > M): A[i - j][j] = M sum - = M else : A[i - j][j] = sum sum - = sum # calculating result for i in range (n): for j in range (n): res + = (i + j + 2 ) * A[i][j] return res # Driver Code if __name__ = = '__main__' : A = [[ 1 , 2 , 3 , 4 ], [ 5 , 6 , 7 , 8 ], [ 9 , 1 , 1 , 2 ], [ 3 , 4 , 5 , 6 ]] m = 9 print (maxMatrix(A, m)) # This code is contributed by 29AjayKumar |
C#
// C# to maximize matrix result using System; public class GFG { static readonly int n = 4; // utility function for maximize matrix result static int maxMatrix( int [,]A, int M) { int sum = 0, res = 0; for ( int i = 0; i < n; i++) { for ( int j = 0; j < n; j++) { sum += A[i,j]; } } // diagonals below longest diagonal // starting from last element of matrix for ( int j = n - 1; j > 0; j--) { for ( int i = 0; i < n - j; i++) { if (sum > M) { A[n - 1 - i,j + i] = M; sum -= M; } else { A[n - 1 - i,j + i] = sum; sum -= sum; } } } // diagonals above longest diagonal for ( int i = n - 1; i >= 0; i--) { for ( int j = 0; j <= i; j++) { if (sum > M) { A[i - j,j] = M; sum -= M; } else { A[i - j,j] = sum; sum -= sum; } } } // calculating result for ( int i = 0; i < n; i++) { for ( int j = 0; j < n; j++) { res += (i + j + 2) * A[i,j]; } } return res; } // driver program static public void Main() { int [,]A= {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 1, 1, 2}, {3, 4, 5, 6}}; int m = 9; Console.Write(maxMatrix(A, m)); } } // This code is contributed by Rajput-Ji |
PHP
<?php // PHP to maximize matrix result $n = 4; // function for maximize // matrix result function maxMatrix( $A , $M ) { global $n ; $sum = 0; $res = 0; for ( $i = 0; $i < $n ; $i ++) for ( $j = 0; $j < $n ; $j ++) $sum += $A [ $i ][ $j ]; // diagonals below longest diagonal // starting from last element of matrix for ( $j = $n - 1; $j > 0; $j --) { for ( $i = 0; $i < $n - $j ; $i ++) { if ( $sum > $M ) { $A [ $n - 1 - $i ][ $j + $i ] = $M ; $sum -= $M ; } else { $A [ $n - 1 - $i ][ $j + i] = $sum ; $sum -= $sum ; } } } // diagonals above longest diagonal for ( $i = $n - 1; $i >= 0; $i --) { for ( $j = 0; $j <= $i ; $j ++) { if ( $sum > $M ) { $A [ $i - $j ][ $j ] = $M ; $sum -= $M ; } else { $A [ $i - $j ][ $j ] = $sum ; $sum -= $sum ; } } } // calculating result for ( $i = 0; $i < $n ; $i ++) { for ( $j = 0; $j < $n ; $j ++) $res += ( $i + $j + 2) * $A [ $i ][ $j ]; } return $res ; } // Driver Code $A = array ( array (1, 2, 3, 4), array (5, 6, 7, 8), array (9, 1, 1, 2), array (3, 4, 5, 6)); $m = 9; echo maxMatrix( $A , $m ); // This code is contributed by anuj_67. ?> |
Javascript
<script> // Javascript to maximize matrix result let n = 4; // utility function for maximize matrix result function maxMatrix(A, M) { let sum = 0, res = 0; for (let i = 0; i < n; i++) { for (let j = 0; j < n; j++) { sum += A[i][j]; } } // diagonals below longest diagonal // starting from last element of matrix for (let j = n - 1; j > 0; j--) { for (let i = 0; i < n - j; i++) { if (sum > M) { A[n - 1 - i][j + i] = M; sum -= M; } else { A[n - 1 - i][j + i] = sum; sum -= sum; } } } // diagonals above longest diagonal for (let i = n - 1; i >= 0; i--) { for (let j = 0; j <= i; j++) { if (sum > M) { A[i - j][j] = M; sum -= M; } else { A[i - j][j] = sum; sum -= sum; } } } // calculating result for (let i = 0; i < n; i++) { for (let j = 0; j < n; j++) { res += (i + j + 2) * A[i][j]; } } return res; } let A = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 1, 1, 2], [3, 4, 5, 6]]; let m = 9; document.write(maxMatrix(A, m)); // This code is contributed by divyesh072019. </script> |
输出:
425
本文由 希瓦姆·普拉丹(anuj_charm) .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以使用 写极客。组织 或者把你的文章寄到contribute@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



