给定一个浮点数x上的函数f(x)和函数根的三个初始不同猜测,求函数根。这里,f(x)可以是代数函数或超越函数。 例如:
null
Input : A function f(x) = x+ 2x
+ 10x - 20 and three initial guesses - 0, 1 and 2 .Output : The value of the root is 1.3688 or any other value within permittable deviation from the root. Input : A function f(x) = x
- 5x + 2 and three initial guesses - 0, 1 and 2 .Output :The value of the root is 0.4021 or any other value within permittable deviation from the root.
穆勒法
Muller方法是一种求根算法,用于求f(x)=0形式的方程的根。1956年,大卫·E·穆勒发现了它。 它从根的三个初始假设开始,然后通过这三个点构造一条抛物线,并将x轴与抛物线的交点作为下一个近似值。这个过程一直持续到找到具有所需精度级别的根为止。
为什么要学习穆勒的方法?
Muller法是寻根法的一种,与对分法、Regula-Falsi法、割线法和Newton-Raphson法一样。但是,与这些方法相比,它有以下一些优势——
- 在Muller方法中,收敛速度(即每一步向根移动的距离)约为1.84,而割线法为1.62,线性法为1,即Regula–falsi法和对分法均为1。所以 Muller方法比二分法、Regula–Falsi法和割线法更快。
- 虽然它比牛顿-拉斐逊法(收敛速度为2)慢,但它克服了牛顿-拉斐逊法的一个最大缺点,即每一步计算导数。
因此,这表明Muller方法是计算函数根的有效方法。
算法及其工作原理
- 假设函数的任意三个不同的初始根为x 0 十、 1. 还有x 2. .
- 现在,通过这些点的函数f(x)的值,画一个二次多项式,即抛物线 0 十、 1. 还有x 2. . 通过这些点的抛物线方程p(x)如下- p(x)=c+b(x–x)
 )+a(x–x)
)+a(x–x)  )
) 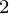 ,其中a、b和c是常数。
,其中a、b和c是常数。
![图片[7]-穆勒法程序-yiteyi-C++库](https://www.yiteyi.com/wp-content/uploads/geeks/geeks_Muller-Method.png)
- 画完这条抛物线,然后找到这条抛物线与x轴的交点,比如x 3. .
- 求抛物线与x轴的交点,即x轴 3. :
- 找到x
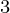 ,p(x)的根,其中p(x)=c+b(x–x)
,p(x)的根,其中p(x)=c+b(x–x)  )+a(x–x)
)+a(x–x)  )
) 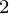 ,使得p(x
,使得p(x 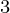 )=c+b(x)
)=c+b(x) 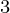 –x
–x  )+a(x)
)+a(x) 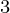 –x
–x  )
) 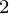 =0,将二次公式应用于p(x)。因为,有两个根,但我们必须取一个更接近x的根
=0,将二次公式应用于p(x)。因为,有两个根,但我们必须取一个更接近x的根  .为避免因附近相等数字的减法而产生舍入误差,请使用以下公式:
.为避免因附近相等数字的减法而产生舍入误差,请使用以下公式: 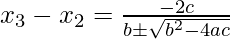 现在,因为,p(x)的根必须更接近x
现在,因为,p(x)的根必须更接近x  ,所以我们必须从上述方程中的两个值中取分母更大的值。
,所以我们必须从上述方程中的两个值中取分母更大的值。 - 要找到上述方程的a、b和c,将x作为x放入p(x)中
 十、
十、 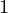 还有x
还有x  ,设这些值为p(x
,设这些值为p(x  ),p(x)
),p(x) 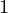 )和p(x)
)和p(x)  ),具体如下:- p(x)
),具体如下:- p(x)  )=c+b(x)
)=c+b(x)  –x
–x  )+a(x)
)+a(x)  –x
–x  )
) 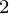 =f(x)
=f(x)  ). p(x)
). p(x) 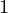 )=c+b(x)
)=c+b(x) 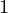 –x
–x  )+a(x)
)+a(x) 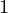 –x
–x  )
) 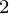 =f(x)
=f(x) 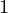 ). p(x)
). p(x)  )=c+b(x)
)=c+b(x)  –x
–x  )+a(x)
)+a(x)  –x
–x  )
) 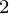 =c=f(x)
=c=f(x)  ).
). - 所以,我们有三个方程和三个变量——a,b,c。通过求解它们,找出这些变量的值,我们得到以下a,b和c的值-
- 找到x
c = p(x) = f(x
) .b = (d
*(h
)
- d
*(h
)
) / ( h
h
* (h
- h
)) .a = (d
*(h
) - d
*(h
)) / ( h
h
* (h
- h
)).
- 哪里 D
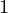 =p(x)
=p(x)  )–p(x)
)–p(x)  )=f(x)
)=f(x)  )-f(x)
)-f(x)  ) D
) D  =p(x)
=p(x) 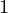 )–p(x)
)–p(x)  )=f(x)
)=f(x) 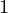 )-f(x)
)-f(x)  ) H
) H 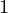 =x
=x  –x
–x  H
H  =x
=x 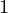 –x
–x 
- 现在,把这些值放到x的表达式中
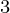 –x
–x  ,并获得x
,并获得x 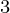 . 这就是p(x)=x的根
. 这就是p(x)=x的根 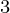 已获得。
已获得。
- 如果x
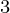 非常接近x
非常接近x  在允许误差范围内,然后x
在允许误差范围内,然后x 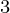 成为f(x)的根,否则,继续重复查找下一个x的过程
成为f(x)的根,否则,继续重复查找下一个x的过程 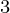 ,与之前的x
,与之前的x 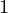 十、
十、  还有x
还有x 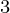 作为新的x
作为新的x  十、
十、 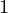 还有x
还有x  .
.
C++
// C++ Program to find root of a function, f(x) #include<bits/stdc++.h> using namespace std; const int MAX_ITERATIONS = 10000; // Function to calculate f(x) float f( float x) { // Taking f(x) = x ^ 3 + 2x ^ 2 + 10x - 20 return 1* pow (x, 3) + 2*x*x + 10*x - 20; } void Muller( float a, float b, float c) { int i; float res; for (i = 0;;++i) { // Calculating various constants required // to calculate x3 float f1 = f(a); float f2 = f(b); float f3 = f(c); float d1 = f1 - f3; float d2 = f2 - f3; float h1 = a - c; float h2 = b - c; float a0 = f3; float a1 = (((d2* pow (h1, 2)) - (d1* pow (h2, 2))) / ((h1*h2) * (h1-h2))); float a2 = (((d1*h2) - (d2*h1))/((h1*h2) * (h1-h2))); float x = ((-2*a0) / (a1 + abs ( sqrt (a1*a1-4*a0*a2)))); float y = ((-2*a0) / (a1- abs ( sqrt (a1*a1-4*a0*a2)))); // Taking the root which is closer to x2 if (x >= y) res = x + c; else res = y + c; // checking for resemblance of x3 with x2 till // two decimal places float m = res*100; float n = c*100; m = floor (m); n = floor (n); if (m == n) break ; a = b; b = c; c = res; if (i > MAX_ITERATIONS) { cout << "Root cannot be found using" << " Muller's method" ; break ; } } if (i <= MAX_ITERATIONS) cout << "The value of the root is " << res; } // Driver main function int main() { float a = 0, b = 1, c = 2; Muller(a, b, c); return 0; } |
JAVA
// Java Program to find root of a function, f(x) import java.io.*; import static java.lang.Math.*; class Muller { static final int MAX_ITERATIONS = 10000 ; // function to calculate f(x) static double f( double x) { // Taking f(x) = x ^ 3 + 2x ^ 2 + 10x - 20 return 1 *pow(x, 3 ) + 2 *x*x + 10 *x - 20 ; } static void Muller( double a, double b, double c) { int i; double res; for (i = 0 ;; ++i) { // Calculating various constants required // to calculate x3 double f1 = f(a); double f2 = f(b); double f3 = f(c); double d1 = f1 - f3; double d2 = f2 - f3; double h1 = a - c; double h2 = b - c; double a0 = f3; double a1 = (((d2*pow(h1, 2 )) - (d1*pow(h2, 2 ))) / ((h1*h2) * (h1-h2))); double a2 = (((d1*h2) - (d2*h1))/((h1*h2) * (h1-h2))); double x = ((- 2 *a0)/(a1 + abs(sqrt(a1*a1- 4 *a0*a2)))); double y = ((- 2 *a0)/(a1-abs(sqrt(a1*a1- 4 *a0*a2)))); // Taking the root which is closer to x2 if (x >= y) res = x + c; else res = y + c; // checking for resemblance of x3 with x2 till // two decimal places double m = res* 100 ; double n = c* 100 ; m = floor(m); n = floor(n); if (m == n) break ; a = b; b = c; c = res; if (i > MAX_ITERATIONS) { System.out.println( "Root cannot be found using" + " Muller's method" ); break ; } } if (i <= MAX_ITERATIONS) System.out.println( "The value of the root is " + res); } // Driver main function public static void main(String args[]) { double a = 0 , b = 1 , c = 2 ; Muller(a, b, c); } } |
Python3
# Python3 Program to find root of # a function, f(x) import math; MAX_ITERATIONS = 10000 ; # Function to calculate f(x) def f(x): # Taking f(x) = x ^ 3 + 2x ^ 2 + 10x - 20 return ( 1 * pow (x, 3 ) + 2 * x * x + 10 * x - 20 ); def Muller(a, b, c): res = 0 ; i = 0 ; while ( True ): # Calculating various constants # required to calculate x3 f1 = f(a); f2 = f(b); f3 = f(c); d1 = f1 - f3; d2 = f2 - f3; h1 = a - c; h2 = b - c; a0 = f3; a1 = (((d2 * pow (h1, 2 )) - (d1 * pow (h2, 2 ))) / ((h1 * h2) * (h1 - h2))); a2 = (((d1 * h2) - (d2 * h1)) / ((h1 * h2) * (h1 - h2))); x = (( - 2 * a0) / (a1 + abs (math.sqrt(a1 * a1 - 4 * a0 * a2)))); y = (( - 2 * a0) / (a1 - abs (math.sqrt(a1 * a1 - 4 * a0 * a2)))); # Taking the root which is # closer to x2 if (x > = y): res = x + c; else : res = y + c; # checking for resemblance of x3 # with x2 till two decimal places m = res * 100 ; n = c * 100 ; m = math.floor(m); n = math.floor(n); if (m = = n): break ; a = b; b = c; c = res; if (i > MAX_ITERATIONS): print ( "Root cannot be found using" , "Muller's method" ); break ; i + = 1 ; if (i < = MAX_ITERATIONS): print ( "The value of the root is" , round (res, 4 )); # Driver Code a = 0 ; b = 1 ; c = 2 ; Muller(a, b, c); # This code is contributed by mits |
C#
// C# Program to find root of a function, f(x) using System; class Muller1 { static int MAX_ITERATIONS = 10000; // function to calculate f(x) static double f( double x) { // Taking f(x) = x ^ 3 + 2x ^ 2 + 10x - 20 return 1*Math.Pow(x, 3) + 2*x*x + 10*x - 20; } static void Muller( double a, double b, double c) { int i; double res; for (i = 0;; ++i) { // Calculating various constants required // to calculate x3 double f1 = f(a); double f2 = f(b); double f3 = f(c); double d1 = f1 - f3; double d2 = f2 - f3; double h1 = a - c; double h2 = b - c; double a0 = f3; double a1 = (((d2*Math.Pow(h1, 2)) - (d1*Math.Pow(h2, 2))) / ((h1*h2) * (h1-h2))); double a2 = (((d1*h2) - (d2*h1))/((h1*h2) * (h1-h2))); double x = ((-2*a0)/(a1 + Math.Abs(Math.Sqrt(a1*a1-4*a0*a2)))); double y = ((-2*a0)/(a1-Math.Abs(Math.Sqrt(a1*a1-4*a0*a2)))); // Taking the root which is closer to x2 if (x >= y) res = x + c; else res = y + c; // checking for resemblance of x3 with x2 till // two decimal places double m = res*100; double n = c*100; m = Math.Floor(m); n = Math.Floor(n); if (m == n) break ; a = b; b = c; c = res; if (i > MAX_ITERATIONS) { Console.WriteLine( "Root cannot be found using" + " Muller's method" ); break ; } } if (i <= MAX_ITERATIONS) Console.WriteLine( "The value of the root is " + Math.Round(res,4)); } // Driver main function static void Main() { double a = 0, b = 1, c = 2; Muller(a, b, c); } } // this code is contributed by mits |
PHP
<?php // PHP Program to find root of a function, f(x) $MAX_ITERATIONS = 10000; // Function to calculate f(x) function f( $x ) { // Taking f(x) = x ^ 3 + 2x ^ 2 + 10x - 20 return 1*pow( $x , 3) + 2* $x * $x + 10* $x - 20; } function Muller( $a , $b , $c ) { global $MAX_ITERATIONS ; $res =0; for ( $i = 0;;++ $i ) { // Calculating various constants required // to calculate x3 $f1 = f( $a ); $f2 = f( $b ); $f3 = f( $c ); $d1 = $f1 - $f3 ; $d2 = $f2 - $f3 ; $h1 = $a - $c ; $h2 = $b - $c ; $a0 = $f3 ; $a1 = ((( $d2 *pow( $h1 , 2)) - ( $d1 *pow( $h2 , 2))) / (( $h1 * $h2 ) * ( $h1 - $h2 ))); $a2 = ((( $d1 * $h2 ) - ( $d2 * $h1 ))/(( $h1 * $h2 ) * ( $h1 - $h2 ))); $x = ((-2* $a0 ) / ( $a1 + abs (sqrt( $a1 * $a1 -4* $a0 * $a2 )))); $y = ((-2* $a0 ) / ( $a1 - abs (sqrt( $a1 * $a1 -4* $a0 * $a2 )))); // Taking the root which is closer to x2 if ( $x >= $y ) $res = $x + $c ; else $res = $y + $c ; // checking for resemblance of x3 with x2 till // two decimal places $m = $res *100; $n = $c *100; $m = floor ( $m ); $n = floor ( $n ); if ( $m == $n ) break ; $a = $b ; $b = $c ; $c = $res ; if ( $i > $MAX_ITERATIONS ) { echo "Root cannot be found using Muller's method" ; break ; } } if ( $i <= $MAX_ITERATIONS ) echo "The value of the root is " . round ( $res ,4); } // Driver main function $a = 0; $b = 1; $c = 2; Muller( $a , $b , $c ); // This code is contributed by mits ?> |
Javascript
<script> // JavaScript Program to find root of a function, f(x) const MAX_ITERATIONS = 10000; // Function to calculate f(x) function f(x) { // Taking f(x) = x ^ 3 + 2x ^ 2 + 10x - 20 return 1*Math.pow(x, 3) + 2*x*x + 10*x - 20; } function Muller(a, b, c) { let i; let res; for (i = 0;;++i) { // Calculating various constants required // to calculate x3 let f1 = f(a); let f2 = f(b); let f3 = f(c); let d1 = f1 - f3; let d2 = f2 - f3; let h1 = a - c; let h2 = b - c; let a0 = f3; let a1 = (((d2*Math.pow(h1, 2)) - (d1*Math.pow(h2, 2))) / ((h1*h2) * (h1-h2))); let a2 = (((d1*h2) - (d2*h1))/((h1*h2) * (h1-h2))); let x = ((-2*a0) / (a1 + Math.abs(Math.sqrt(a1*a1-4*a0*a2)))); let y = ((-2*a0) / (a1-Math.abs(Math.sqrt(a1*a1-4*a0*a2)))); // Taking the root which is closer to x2 if (x >= y) res = x + c; else res = y + c; // checking for resemblance of x3 with x2 till // two decimal places let m = res*100; let n = c*100; m = Math.floor(m); n = Math.floor(n); if (m == n) break ; a = b; b = c; c = res; if (i > MAX_ITERATIONS) { document.write( "Root cannot be found using" + " Muller's method" ); break ; } } if (i <= MAX_ITERATIONS) document.write( "The value of the root is " + res.toFixed(4)); } // Driver main function let a = 0, b = 1, c = 2; Muller(a, b, c); // This code is contributed by Surbhi Tyagi. </script> |
输出:
The value of the root is 1.3688
优势
- 可以找到假想的根。
- 不需要寻找衍生品。
缺点
- 长时间手工操作,更容易出错。
- 可以找到外来的根。
参考文献-
- B.S.格雷瓦尔的《高等工程数学》。
本文由 辛格先生 .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以使用 贡献极客。组织 或者把你的文章寄到contribute@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



