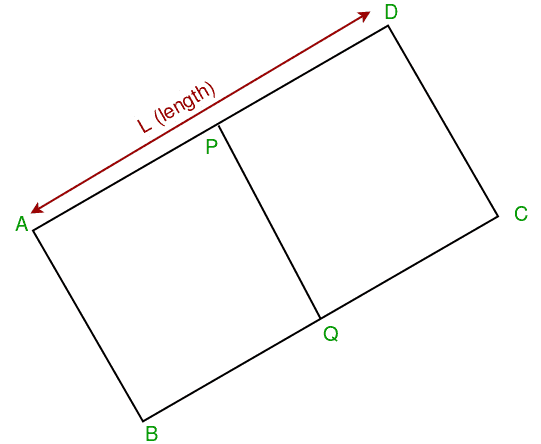
考虑矩形ABCD,我们给出了侧AD和BC(P和Q分别)的中间点以及它们的长度L(AD=BC=L)的坐标。现在给定参数,我们需要打印4个点A、B、C和D的坐标。
null
例如:
Input : p = (1, 0) q = (1, 2) L = 2Output : (0, 0), (0, 2), (2, 2), (2, 0)Explanation:The printed points form a rectangle whichsatisfy the input constraints.Input : p = (1, 1) q = (-1, -1) L = 2*sqrt(2)Output : (0, 2), (-2, 0), (0, -2), (2, 0)
问题陈述中可能出现3种情况:
- 矩形是水平的,即AD和BC平行于X轴
- 矩形是垂直的,即AD和BC平行于Y轴
- 矩形与轴线成一定角度倾斜
前两种情况很简单,可以使用基本几何轻松解决。对于第三种情况,我们需要应用一些数学概念来找到这些点。
为了清楚起见,请考虑上面的图表。我们有p和q的坐标。因此我们可以找到AD和BC的斜率(因为pq垂直于AD)。一旦我们有了AD的斜率,我们就可以找到通过AD的直线方程。现在我们可以应用距离公式来获得沿X和Y轴的位移。
If slope of AD = m, thenm = (p.x- q.x)/(q.y - p.y)and displacement along X axis, dx = L/(2*sqrt(1+m*m))Similarly, dy = m*L/(2*sqrt(1+m*m))
现在我们可以简单地通过简单地加上和减去相应的位移来求出四个角的坐标。
下面是实现。
C++
// C++ program to find corner points of // a rectangle using given length and middle // points. #include <bits/stdc++.h> using namespace std; // Structure to represent a co-ordinate point struct Point { float x, y; Point() { x = y = 0; } Point( float a, float b) { x = a, y = b; } }; // This function receives two points and length // of the side of rectangle and prints the 4 // corner points of the rectangle void printCorners(Point p, Point q, float l) { Point a, b, c, d; // horizontal rectangle if (p.x == q.x) { a.x = p.x - (l/2.0); a.y = p.y; d.x = p.x + (l/2.0); d.y = p.y; b.x = q.x - (l/2.0); b.y = q.y; c.x = q.x + (l/2.0); c.y = q.y; } // vertical rectangle else if (p.y == q.y) { a.y = p.y - (l/2.0); a.x = p.x; d.y = p.y + (l/2.0); d.x = p.x; b.y = q.y - (l/2.0); b.x = q.x; c.y = q.y + (l/2.0); c.x = q.x; } // slanted rectangle else { // calculate slope of the side float m = (p.x-q.x)/ float (q.y-p.y); // calculate displacements along axes float dx = (l / sqrt (1+(m*m))) *0.5 ; float dy = m*dx; a.x = p.x - dx; a.y = p.y - dy; d.x = p.x + dx; d.y = p.y + dy; b.x = q.x - dx; b.y = q.y - dy; c.x = q.x + dx; c.y = q.y + dy; } cout << a.x << ", " << a.y << " n" << b.x << ", " << b.y << "n" ; << c.x << ", " << c.y << " n" << d.x << ", " << d.y << "nn" ; } // Driver code int main() { Point p1(1, 0), q1(1, 2); printCorners(p1, q1, 2); Point p(1, 1), q(-1, -1); printCorners(p, q, 2* sqrt (2)); return 0; } |
JAVA
// Java program to find corner points of // a rectangle using given length and middle // points. class GFG { // Structure to represent a co-ordinate point static class Point { float x, y; Point() { x = y = 0 ; } Point( float a, float b) { x = a; y = b; } }; // This function receives two points and length // of the side of rectangle and prints the 4 // corner points of the rectangle static void printCorners(Point p, Point q, float l) { Point a = new Point(), b = new Point(), c = new Point(), d = new Point(); // horizontal rectangle if (p.x == q.x) { a.x = ( float ) (p.x - (l / 2.0 )); a.y = p.y; d.x = ( float ) (p.x + (l / 2.0 )); d.y = p.y; b.x = ( float ) (q.x - (l / 2.0 )); b.y = q.y; c.x = ( float ) (q.x + (l / 2.0 )); c.y = q.y; } // vertical rectangle else if (p.y == q.y) { a.y = ( float ) (p.y - (l / 2.0 )); a.x = p.x; d.y = ( float ) (p.y + (l / 2.0 )); d.x = p.x; b.y = ( float ) (q.y - (l / 2.0 )); b.x = q.x; c.y = ( float ) (q.y + (l / 2.0 )); c.x = q.x; } // slanted rectangle else { // calculate slope of the side float m = (p.x - q.x) / (q.y - p.y); // calculate displacements along axes float dx = ( float ) ((l / Math.sqrt( 1 + (m * m))) * 0.5 ); float dy = m * dx; a.x = p.x - dx; a.y = p.y - dy; d.x = p.x + dx; d.y = p.y + dy; b.x = q.x - dx; b.y = q.y - dy; c.x = q.x + dx; c.y = q.y + dy; } System.out.print(( int )a.x + ", " + ( int )a.y + " " + ( int )b.x + ", " + ( int )b.y + "" + ( int )c.x + ", " + ( int )c.y + " " + ( int )d.x + ", " + ( int )d.y + "" ); } // Driver code public static void main(String[] args) { Point p1 = new Point( 1 , 0 ), q1 = new Point( 1 , 2 ); printCorners(p1, q1, 2 ); Point p = new Point( 1 , 1 ), q = new Point(- 1 , - 1 ); printCorners(p, q, ( float ) ( 2 * Math.sqrt( 2 ))); } } // This code contributed by Rajput-Ji |
Python3
# Python3 program to find corner points of # a rectangle using given length and middle # points. import math # Structure to represent a co-ordinate point class Point: def __init__( self , a = 0 , b = 0 ): self .x = a self .y = b # This function receives two points and length # of the side of rectangle and prints the 4 # corner points of the rectangle def printCorners(p, q, l): a, b, c, d = Point(), Point(), Point(), Point() # Horizontal rectangle if (p.x = = q.x): a.x = p.x - (l / 2.0 ) a.y = p.y d.x = p.x + (l / 2.0 ) d.y = p.y b.x = q.x - (l / 2.0 ) b.y = q.y c.x = q.x + (l / 2.0 ) c.y = q.y # Vertical rectangle elif (p.y = = q.y): a.y = p.y - (l / 2.0 ) a.x = p.x d.y = p.y + (l / 2.0 ) d.x = p.x b.y = q.y - (l / 2.0 ) b.x = q.x c.y = q.y + (l / 2.0 ) c.x = q.x # Slanted rectangle else : # Calculate slope of the side m = (p.x - q.x) / (q.y - p.y) # Calculate displacements along axes dx = (l / math.sqrt( 1 + (m * m))) * 0.5 dy = m * dx a.x = p.x - dx a.y = p.y - dy d.x = p.x + dx d.y = p.y + dy b.x = q.x - dx b.y = q.y - dy c.x = q.x + dx c.y = q.y + dy print ( int (a.x), ", " , int (a.y), sep = "") print ( int (b.x), ", " , int (b.y), sep = "") print ( int (c.x), ", " , int (c.y), sep = "") print ( int (d.x), ", " , int (d.y), sep = "") print () # Driver code p1 = Point( 1 , 0 ) q1 = Point( 1 , 2 ) printCorners(p1, q1, 2 ) p = Point( 1 , 1 ) q = Point( - 1 , - 1 ) printCorners(p, q, 2 * math.sqrt( 2 )) # This code is contributed by shubhamsingh10 |
C#
// C# program to find corner points of // a rectangle using given length and middle // points. using System; class GFG { // Structure to represent a co-ordinate point public class Point { public float x, y; public Point() { x = y = 0; } public Point( float a, float b) { x = a; y = b; } }; // This function receives two points and length // of the side of rectangle and prints the 4 // corner points of the rectangle static void printCorners(Point p, Point q, float l) { Point a = new Point(), b = new Point(), c = new Point(), d = new Point(); // horizontal rectangle if (p.x == q.x) { a.x = ( float ) (p.x - (l / 2.0)); a.y = p.y; d.x = ( float ) (p.x + (l / 2.0)); d.y = p.y; b.x = ( float ) (q.x - (l / 2.0)); b.y = q.y; c.x = ( float ) (q.x + (l / 2.0)); c.y = q.y; } // vertical rectangle else if (p.y == q.y) { a.y = ( float ) (p.y - (l / 2.0)); a.x = p.x; d.y = ( float ) (p.y + (l / 2.0)); d.x = p.x; b.y = ( float ) (q.y - (l / 2.0)); b.x = q.x; c.y = ( float ) (q.y + (l / 2.0)); c.x = q.x; } // slanted rectangle else { // calculate slope of the side float m = (p.x - q.x) / (q.y - p.y); // calculate displacements along axes float dx = ( float ) ((l / Math.Sqrt(1 + (m * m))) * 0.5); float dy = m * dx; a.x = p.x - dx; a.y = p.y - dy; d.x = p.x + dx; d.y = p.y + dy; b.x = q.x - dx; b.y = q.y - dy; c.x = q.x + dx; c.y = q.y + dy; } Console.Write(( int )a.x + ", " + ( int )a.y + " " + ( int )b.x + ", " + ( int )b.y + "" + ( int )c.x + ", " + ( int )c.y + " " + ( int )d.x + ", " + ( int )d.y + "" ); } // Driver code public static void Main(String[] args) { Point p1 = new Point(1, 0), q1 = new Point(1, 2); printCorners(p1, q1, 2); Point p = new Point(1, 1), q = new Point(-1, -1); printCorners(p, q, ( float ) (2 * Math.Sqrt(2))); } } // This code has been contributed by 29AjayKumar |
Javascript
<script> // Javascript program to find corner points of // a rectangle using given length and middle // points. // Structure to represent a co-ordinate point class Point { constructor(a,b) { this .x=a; this .y=b; } } // This function receives two points and length // of the side of rectangle and prints the 4 // corner points of the rectangle function printCorners(p,q,l) { let a = new Point(), b = new Point(), c = new Point(), d = new Point(); // horizontal rectangle if (p.x == q.x) { a.x = (p.x - (l / 2.0)); a.y = p.y; d.x = (p.x + (l / 2.0)); d.y = p.y; b.x = (q.x - (l / 2.0)); b.y = q.y; c.x = (q.x + (l / 2.0)); c.y = q.y; } // vertical rectangle else if (p.y == q.y) { a.y = (p.y - (l / 2.0)); a.x = p.x; d.y = (p.y + (l / 2.0)); d.x = p.x; b.y = (q.y - (l / 2.0)); b.x = q.x; c.y = (q.y + (l / 2.0)); c.x = q.x; } // slanted rectangle else { // calculate slope of the side let m = (p.x - q.x) / (q.y - p.y); // calculate displacements along axes let dx = ((l / Math.sqrt(1 + (m * m))) * 0.5); let dy = m * dx; a.x = p.x - dx; a.y = p.y - dy; d.x = p.x + dx; d.y = p.y + dy; b.x = q.x - dx; b.y = q.y - dy; c.x = q.x + dx; c.y = q.y + dy; } document.write(a.x + ", " + a.y + " <br>" + b.x + ", " + b.y + "<br>" + c.x + ", " + c.y + " <br>" + d.x + ", " + d.y + "<br>" ); } // Driver code let p1 = new Point(1, 0), q1 = new Point(1, 2); printCorners(p1, q1, 2); let p = new Point(1, 1), q = new Point(-1, -1); printCorners(p, q, (2 * Math.sqrt(2))); // This code is contributed by rag2127 </script> |
输出:
0, 0 0, 22, 2 2, 00, 2 -2, 00, -2 2, 0
参考: 堆垛溢出 本文由 阿什图什·库马尔 如果你喜欢Geeksforgek,并且想贡献自己的力量,你也可以使用 写极客。组织 或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



