给定两个字符串S和T,求S中不是T中的子序列的最短子序列的长度。如果不可能有这样的子序列,则返回-1。子序列是以相同的相对顺序出现的序列,但不一定是连续的。长度为n的字符串有2^n个不同的可能子序列。 长度为m(1<=m<=1000)的字符串S 长度为n(1<=n<=1000)的字符串T 例如:
Input : S = “babab” T = “babba”Output : 3The subsequence “aab” of length 3 is present in S but not in T.Input : S = “abb” T = “abab”Output : -1There is no subsequence that is present in S but not in T.
蛮力法 一种简单的方法是生成字符串S的所有子序列,并为每个子序列检查它是否存在于字符串T中。考虑S==ABB的例子2, 它的子序列是“,”a“,”b“,”ab“,”bb“,”abb“,每一个都出现在“abab”中。这个解决方案的时间复杂度将是指数级的。 高效(动态规划) 1.最优子结构: 考虑长度为m和n的两个字符串S和T,并让函数找到最短的不寻常子序列为Trestesteq(char *s,char *t)。对于S中的每个字符,如果它不在T中,那么这个字符就是答案本身。 否则,如果它是在索引k处发现的,那么我们可以选择是否将其包含在最短的不寻常子序列中。
If it is included answer = 1 + ShortestSeq( S + 1, T + k + 1) If not included answer = ShortestSeq( S + 1, T) The minimum of the two is the answer.
因此,我们可以看到这个问题具有最优子结构性质,因为它可以通过使用子问题的解来解决。 2.重叠子问题 下面是上述问题的简单递归实现。
C++
// A simple recursive C++ program to find shortest // uncommon subsequence. #include<bits/stdc++.h> using namespace std; #define MAX 1005 /* A recursive function to find the length of shortest uncommon subsequence*/ int shortestSeq( char *S, char *T, int m, int n) { // S string is empty if (m == 0) return MAX; // T string is empty if (n <= 0) return 1; // Loop to search for current character int k; for (k=0; k < n; k++) if (T[k] == S[0]) break ; // char not found in T if (k == n) return 1; // Return minimum of following two // Not including current char in answer // Including current char return min(shortestSeq(S+1, T, m-1, n), 1 + shortestSeq(S+1, T+k+1, m-1, n-k-1)); } // Driver program to test the above function int main() { char S[] = "babab" ; char T[] = "babba" ; int m = strlen (S), n = strlen (T); int ans = shortestSeq(S, T, m, n); if (ans >= MAX) ans = -1; cout << "Length of shortest subsequence is: " << ans << endl; return 0; } |
JAVA
// A simple recursive Java program to find shortest // uncommon subsequence. import java.util.*; class GFG { static final int MAX = 1005 ; /* A recursive function to find the length of shortest uncommon subsequence*/ static int shortestSeq( char []S, char []T, int m, int n) { // S String is empty if (m == 0 ) return MAX; // T String is empty if (n <= 0 ) return 1 ; // Loop to search for current character int k; for (k = 0 ; k < n; k++) if (T[k] == S[ 0 ]) break ; // char not found in T if (k == n) return 1 ; // Return minimum of following two // Not including current char in answer // Including current char return Math.min(shortestSeq(Arrays.copyOfRange(S, 1 , S.length), T, m - 1 , n), 1 + shortestSeq(Arrays.copyOfRange(S, 1 , S.length), Arrays.copyOfRange(T, k + 1 , T.length), m - 1 , n - k - 1 )); } // Driver code public static void main(String[] args) { char S[] = "babab" .toCharArray(); char T[] = "babba" .toCharArray(); int m = S.length, n = T.length; int ans = shortestSeq(S, T, m, n); if (ans >= MAX) ans = - 1 ; System.out.print( "Length of shortest subsequence is: " + ans + "" ); } } // This code is contributed by Rajput-Ji |
Python3
# A simple recursive Python # program to find shortest # uncommon subsequence. MAX = 1005 # A recursive function to # find the length of shortest # uncommon subsequence def shortestSeq(S, T, m, n): # S String is empty if m = = 0 : return MAX # T String is empty if (n < = 0 ): return 1 # Loop to search for # current character for k in range (n): if (T[k] = = S[ 0 ]): break # char not found in T if (k = = n): return 1 # Return minimum of following # two Not including current # char in answer Including # current char return min (shortestSeq(S[ 1 : ], T, m - 1 , n), 1 + shortestSeq((S[ 1 : ]), T[k + 1 : ], m - 1 , n - k - 1 )) # Driver code S = "babab" T = "babba" m = len (S) n = len (T) ans = shortestSeq(S, T, m, n) if (ans > = MAX ): ans = - 1 print ( "Length of shortest subsequence is:" , ans) # This code is contributed by avanitrachhadiya2155 |
C#
// A simple recursive C# program to find shortest // uncommon subsequence. using System; class GFG { static readonly int MAX = 1005; /* A recursive function to find the length of shortest uncommon subsequence*/ static int shortestSeq( char []S, char []T, int m, int n) { // S String is empty if (m == 0) return MAX; // T String is empty if (n <= 0) return 1; // Loop to search for current character int k; for (k = 0; k < n; k++) if (T[k] == S[0]) break ; // char not found in T if (k == n) return 1; // Return minimum of following two // Not including current char in answer // Including current char char []St1 = new Char[S.Length - 1]; Array.Copy(S, 1, St1, 0, S.Length - 1); char []St2 = new Char[S.Length - 1]; Array.Copy(S, 1, St2, 0, S.Length - 1); char []Tt1 = new Char[T.Length - (k + 1)]; Array.Copy(T, k + 1, Tt1, 0, T.Length - (k + 1)); return Math.Min(shortestSeq(St1, T, m - 1, n), 1 + shortestSeq(St2, Tt1, m - 1, n - k - 1)); } // Driver code public static void Main(String[] args) { char []S = "babab" .ToCharArray(); char []T = "babba" .ToCharArray(); int m = S.Length, n = T.Length; int ans = shortestSeq(S, T, m, n); if (ans >= MAX) ans = -1; Console.Write( "Length of shortest subsequence is: " + ans + "" ); } } // This code is contributed by Rajput-Ji |
输出:
Length of shortest subsequence is : 3
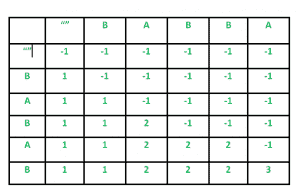
如果我们画出完整的递归树,那么我们可以看到有许多子问题被一次又一次地解决。因此,该问题具有重叠子结构性质,可以通过记忆或制表的方式避免对相同子问题的重新计算。以下是该问题的列表实现。
C++
// A dynamic programming based C++ program // to find shortest uncommon subsequence. #include<bits/stdc++.h> using namespace std; #define MAX 1005 // Returns length of shortest common subsequence int shortestSeq( char *S, char *T) { int m = strlen (S), n = strlen (T); // declaring 2D array of m + 1 rows and // n + 1 columns dynamically int dp[m+1][n+1]; // T string is empty for ( int i = 0; i <= m; i++) dp[i][0] = 1; // S string is empty for ( int i = 0; i <= n; i++) dp[0][i] = MAX; for ( int i = 1; i <= m; i++) { for ( int j = 1; j <= n; j++) { char ch = S[i-1]; int k; for (k = j-1; k >= 0; k--) if (T[k] == ch) break ; // char not present in T if (k == -1) dp[i][j] = 1; else dp[i][j] = min(dp[i-1][j], dp[i-1][k] + 1); } } int ans = dp[m][n]; if (ans >= MAX) ans = -1; return ans; } // Driver program to test the above function int main() { char S[] = "babab" ; char T[] = "babba" ; int m = strlen (S), n = strlen (T); cout << "Length of shortest subsequence is : " << shortestSeq(S, T) << endl; } |
JAVA
// A dynamic programming based Java program // to find shortest uncommon subsequence. class GFG { static final int MAX = 1005 ; // Returns length of shortest common subsequence static int shortestSeq( char [] S, char [] T) { int m = S.length, n = T.length; // declaring 2D array of m + 1 rows and // n + 1 columns dynamically int dp[][] = new int [m + 1 ][n + 1 ]; // T string is empty for ( int i = 0 ; i <= m; i++) { dp[i][ 0 ] = 1 ; } // S string is empty for ( int i = 0 ; i <= n; i++) { dp[ 0 ][i] = MAX; } for ( int i = 1 ; i <= m; i++) { for ( int j = 1 ; j <= n; j++) { char ch = S[i - 1 ]; int k; for (k = j - 1 ; k >= 0 ; k--) { if (T[k] == ch) { break ; } } // char not present in T if (k == - 1 ) { dp[i][j] = 1 ; } else { dp[i][j] = Math.min(dp[i - 1 ][j], dp[i - 1 ][k] + 1 ); } } } int ans = dp[m][n]; if (ans >= MAX) { ans = - 1 ; } return ans; } // Driver code public static void main(String[] args) { char S[] = "babab" .toCharArray(); char T[] = "babba" .toCharArray(); int m = S.length, n = T.length; System.out.println( "Length of shortest" + "subsequence is : " + shortestSeq(S, T)); } } // This code is contributed by 29AjayKumar |
Python3
# A dynamic programming based Python program # to find shortest uncommon subsequence. MAX = 1005 # Returns length of shortest common subsequence def shortestSeq(S: list , T: list ): m = len (S) n = len (T) # declaring 2D array of m + 1 rows and # n + 1 columns dynamically dp = [[ 0 for i in range (n + 1 )] for j in range (m + 1 )] # T string is empty for i in range (m + 1 ): dp[i][ 0 ] = 1 # S string is empty for i in range (n + 1 ): dp[ 0 ][i] = MAX for i in range ( 1 , m + 1 ): for j in range ( 1 , n + 1 ): ch = S[i - 1 ] k = j - 1 while k > = 0 : if T[k] = = ch: break k - = 1 # char not present in T if k = = - 1 : dp[i][j] = 1 else : dp[i][j] = min (dp[i - 1 ][j], dp[i - 1 ][k] + 1 ) ans = dp[m][n] if ans > = MAX : ans = - 1 return ans # Driver Code if __name__ = = "__main__" : S = "babab" T = "babba" print ( "Length of shortest subsequence is:" , shortestSeq(S, T)) # This code is contributed by # sanjeev2552 |
C#
// A dynamic programming based C# program // to find shortest uncommon subsequence. using System; class GFG { static readonly int MAX = 1005; // Returns length of shortest common subsequence static int shortestSeq( char [] S, char [] T) { int m = S.Length, n = T.Length; // declaring 2D array of m + 1 rows and // n + 1 columns dynamically int [,]dp = new int [m + 1, n + 1]; // T string is empty for ( int i = 0; i <= m; i++) { dp[i, 0] = 1; } // S string is empty for ( int i = 0; i <= n; i++) { dp[0, i] = MAX; } for ( int i = 1; i <= m; i++) { for ( int j = 1; j <= n; j++) { char ch = S[i - 1]; int k; for (k = j - 1; k >= 0; k--) { if (T[k] == ch) { break ; } } // char not present in T if (k == -1) { dp[i, j] = 1; } else { dp[i, j] = Math.Min(dp[i - 1, j], dp[i - 1, k] + 1); } } } int ans = dp[m, n]; if (ans >= MAX) { ans = -1; } return ans; } // Driver code public static void Main(String[] args) { char []S = "babab" .ToCharArray(); char []T = "babba" .ToCharArray(); int m = S.Length, n = T.Length; Console.WriteLine( "Length of shortest" + "subsequence is : " + shortestSeq(S, T)); } } // This code contributed by Rajput-Ji |
PHP
<?php // A dynamic programming based PHP program // to find shortest uncommon subsequence. $GLOBALS [ 'MAX' ] = 1005; // Returns length of shortest // common subsequence function shortestSeq( $S , $T ) { $m = strlen ( $S ); $n = strlen ( $T ); // declaring 2D array of m + 1 rows // and n + 1 columns dynamically $dp = array ( array ()); // T string is empty for ( $i = 0; $i <= $m ; $i ++) $dp [ $i ][0] = 1; // S string is empty for ( $i = 0; $i <= $n ; $i ++) $dp [0][ $i ] = $GLOBALS [ 'MAX' ]; for ( $i = 1; $i <= $m ; $i ++) { for ( $j = 1; $j <= $n ; $j ++) { $ch = $S [ $i - 1]; for ( $k = $j - 1; $k >= 0; $k --) if ( $T [ $k ] == $ch ) break ; // char not present in T if ( $k == -1) $dp [ $i ][ $j ] = 1; else $dp [ $i ][ $j ] = min( $dp [ $i - 1][ $j ], $dp [ $i - 1][ $k ] + 1); } } $ans = $dp [ $m ][ $n ]; if ( $ans >= $GLOBALS [ 'MAX' ]) $ans = -1; return $ans ; } // Driver Code $S = "babab" ; $T = "babba" ; $m = strlen ( $S ); $n = strlen ( $T ); echo "Length of shortest subsequence is : " , shortestSeq( $S , $T ); // This code is contributed by Ryuga ?> |
输出:
Length of shortest subsequence is : 3
时间复杂性: O(mn^2) 空间复杂性: O(明尼苏达州) 本文由 阿迪蒂·夏尔马 .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以使用 贡献极客。组织 或者把你的文章寄到contribute@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



