给定三角形在二维平面上所有三个顶点的坐标,任务是找到所有三个角度。 例子:
null
Input : A = (0, 0), B = (0, 1), C = (1, 0)Output : 90, 45, 45
为了解决这个问题,我们使用下面的方法 余弦定律 .
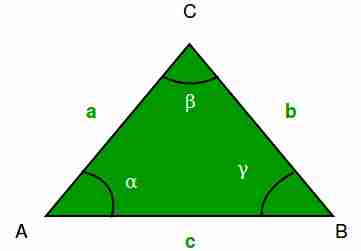
c^2 = a^2 + b^2 - 2(a)(b)(cos beta)
重新安排之后
beta = acos( ( a^2 + b^2 - c^2 ) / (2ab) )
在三角学中,余弦定律(也称为余弦公式或余弦规则)将三角形边的长度与其中一个角的余弦联系起来。
First, calculate the length of all the sides. Then apply above formula to get all angles in radian. Then convert angles from radian into degrees.
以下是上述步骤的实施。
C++
// Code to find all three angles // of a triangle given coordinate // of all three vertices #include <iostream> #include <utility> // for pair #include <cmath> // for math functions using namespace std; #define PI 3.1415926535 // returns square of distance b/w two points int lengthSquare(pair< int , int > X, pair< int , int > Y) { int xDiff = X.first - Y.first; int yDiff = X.second - Y.second; return xDiff*xDiff + yDiff*yDiff; } void printAngle(pair< int , int > A, pair< int , int > B, pair< int , int > C) { // Square of lengths be a2, b2, c2 int a2 = lengthSquare(B,C); int b2 = lengthSquare(A,C); int c2 = lengthSquare(A,B); // length of sides be a, b, c float a = sqrt (a2); float b = sqrt (b2); float c = sqrt (c2); // From Cosine law float alpha = acos ((b2 + c2 - a2)/(2*b*c)); float beta = acos ((a2 + c2 - b2)/(2*a*c)); float gamma = acos ((a2 + b2 - c2)/(2*a*b)); // Converting to degree alpha = alpha * 180 / PI; beta = beta * 180 / PI; gamma = gamma * 180 / PI; // printing all the angles cout << "alpha : " << alpha << endl; cout << "beta : " << beta << endl; cout << "gamma : " << gamma << endl; } // Driver code int main() { pair< int , int > A = make_pair(0,0); pair< int , int > B = make_pair(0,1); pair< int , int > C = make_pair(1,0); printAngle(A,B,C); return 0; } |
JAVA
// Java Code to find all three angles // of a triangle given coordinate // of all three vertices import java.awt.Point; import static java.lang.Math.PI; import static java.lang.Math.sqrt; import static java.lang.Math.acos; class Test { // returns square of distance b/w two points static int lengthSquare(Point p1, Point p2) { int xDiff = p1.x- p2.x; int yDiff = p1.y- p2.y; return xDiff*xDiff + yDiff*yDiff; } static void printAngle(Point A, Point B, Point C) { // Square of lengths be a2, b2, c2 int a2 = lengthSquare(B,C); int b2 = lengthSquare(A,C); int c2 = lengthSquare(A,B); // length of sides be a, b, c float a = ( float )sqrt(a2); float b = ( float )sqrt(b2); float c = ( float )sqrt(c2); // From Cosine law float alpha = ( float ) acos((b2 + c2 - a2)/( 2 *b*c)); float betta = ( float ) acos((a2 + c2 - b2)/( 2 *a*c)); float gamma = ( float ) acos((a2 + b2 - c2)/( 2 *a*b)); // Converting to degree alpha = ( float ) (alpha * 180 / PI); betta = ( float ) (betta * 180 / PI); gamma = ( float ) (gamma * 180 / PI); // printing all the angles System.out.println( "alpha : " + alpha); System.out.println( "betta : " + betta); System.out.println( "gamma : " + gamma); } // Driver method public static void main(String[] args) { Point A = new Point( 0 , 0 ); Point B = new Point( 0 , 1 ); Point C = new Point( 1 , 0 ); printAngle(A,B,C); } } |
Python3
# Python3 code to find all three angles # of a triangle given coordinate # of all three vertices import math # returns square of distance b/w two points def lengthSquare(X, Y): xDiff = X[ 0 ] - Y[ 0 ] yDiff = X[ 1 ] - Y[ 1 ] return xDiff * xDiff + yDiff * yDiff def printAngle(A, B, C): # Square of lengths be a2, b2, c2 a2 = lengthSquare(B, C) b2 = lengthSquare(A, C) c2 = lengthSquare(A, B) # length of sides be a, b, c a = math.sqrt(a2); b = math.sqrt(b2); c = math.sqrt(c2); # From Cosine law alpha = math.acos((b2 + c2 - a2) / ( 2 * b * c)); betta = math.acos((a2 + c2 - b2) / ( 2 * a * c)); gamma = math.acos((a2 + b2 - c2) / ( 2 * a * b)); # Converting to degree alpha = alpha * 180 / math.pi; betta = betta * 180 / math.pi; gamma = gamma * 180 / math.pi; # printing all the angles print ( "alpha : %f" % (alpha)) print ( "betta : %f" % (betta)) print ( "gamma : %f" % (gamma)) # Driver code A = ( 0 , 0 ) B = ( 0 , 1 ) C = ( 1 , 0 ) printAngle(A, B, C); # This code is contributed # by ApurvaRaj |
C#
// C# Code to find all three angles // of a triangle given coordinate // of all three vertices using System; class GFG { class Point { public int x, y; public Point( int x, int y) { this .x = x; this .y = y; } } // returns square of distance b/w two points static int lengthSquare(Point p1, Point p2) { int xDiff = p1.x - p2.x; int yDiff = p1.y - p2.y; return xDiff * xDiff + yDiff * yDiff; } static void printAngle(Point A, Point B, Point C) { // Square of lengths be a2, b2, c2 int a2 = lengthSquare(B, C); int b2 = lengthSquare(A, C); int c2 = lengthSquare(A, B); // length of sides be a, b, c float a = ( float )Math.Sqrt(a2); float b = ( float )Math.Sqrt(b2); float c = ( float )Math.Sqrt(c2); // From Cosine law float alpha = ( float ) Math.Acos((b2 + c2 - a2) / (2 * b * c)); float betta = ( float ) Math.Acos((a2 + c2 - b2) / (2 * a * c)); float gamma = ( float ) Math.Acos((a2 + b2 - c2) / (2 * a * b)); // Converting to degree alpha = ( float ) (alpha * 180 / Math.PI); betta = ( float ) (betta * 180 / Math.PI); gamma = ( float ) (gamma * 180 / Math.PI); // printing all the angles Console.WriteLine( "alpha : " + alpha); Console.WriteLine( "betta : " + betta); Console.WriteLine( "gamma : " + gamma); } // Driver Code public static void Main(String[] args) { Point A = new Point(0, 0); Point B = new Point(0, 1); Point C = new Point(1, 0); printAngle(A, B, C); } } // This code is contributed by Rajput-Ji |
输出:
alpha : 90beta : 45gamma : 45
参考 : https://en.wikipedia.org/wiki/Law_of_cosines 本文由 普拉提克·切哈杰 .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以使用 写极客。组织 或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



